
Hello, and welcome to this video on inverse trig functions!
Normal Trig Functions
In order to understand what inverse trig functions are, let’s first review what normal trigonometric functions are.
Remember, the common three trig functions are sine, cosine, and tangent. These trig functions are used to relate a triangle’s side and angle measures to one another.
For instance, we would use tangent in a problem where we need to find the missing side length of a triangle.

SOHCAHTOA
If we remember SOH-CAH-TOA, we can see that this triangle uses TOA, which stands for \(\tan{\theta} =\frac{opposite}{adjacent} \).
Example #1
If we plug in the values for our triangle, we get \(\tan {30} =\frac{3}{x}\).
Rearranging to get \(x\) by itself gives us \(x=\frac{3}{tan 30}\).
This then simplifies to \(x\approx 5.20\).
Example #2
But what if we are given a triangle where we know the side measures but we want to know the angle measure, like this:
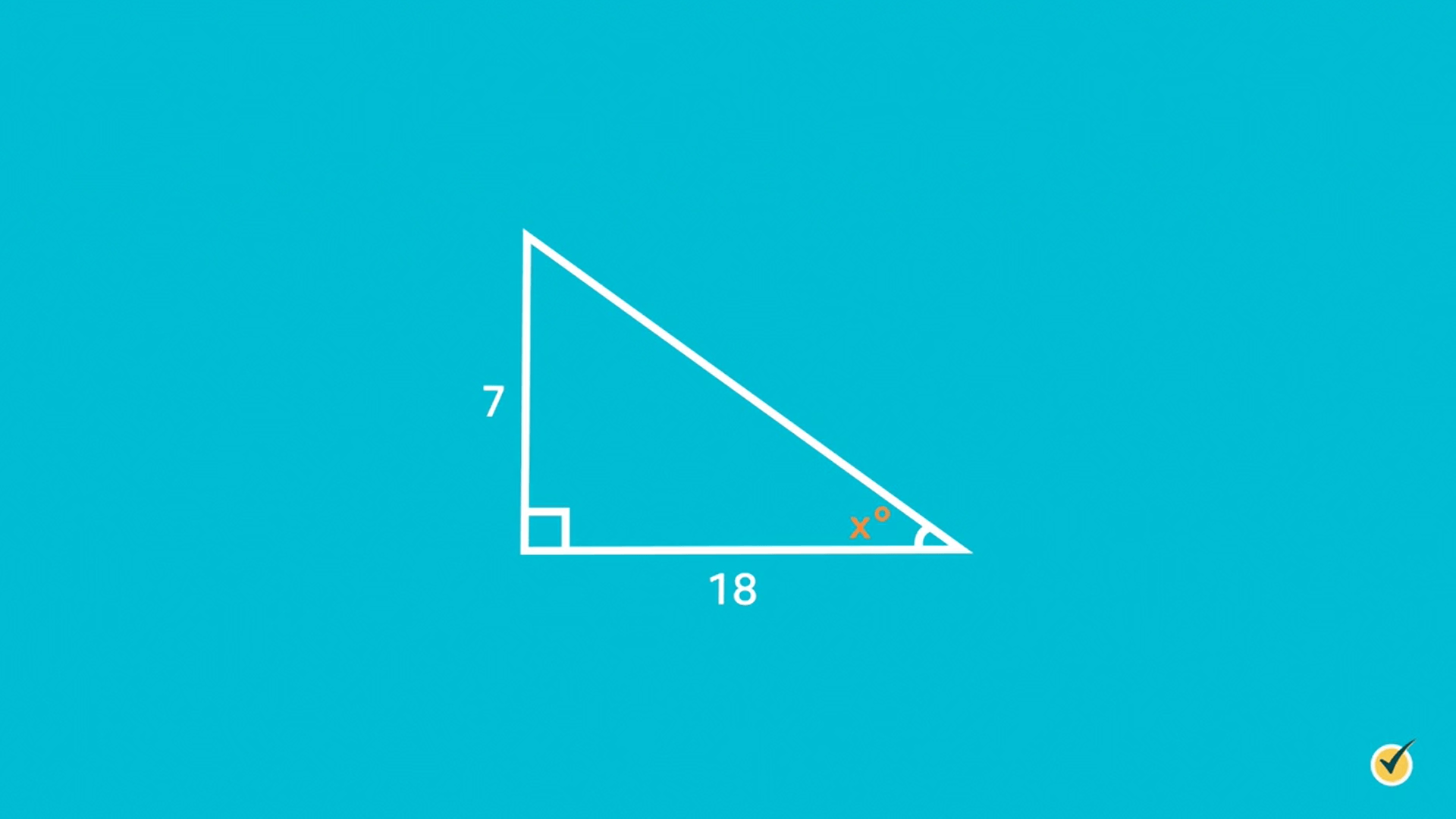
If we plug it into our TOA equation, we get \(tan x =\frac{7}{18}\).
We want to get the \(x\)-value by itself, so we need to “undo” the tangent somehow. This is where inverse trig functions come in handy. Inverse trig functions are just the opposite of trig functions.
The inverse of tangent is written as: \(\arctan{x}\) (which can look like \(\text{atan }x\)) or \(\tan^{-1}{x}\) (or tan inverse \(x\)). Sine and cosine work the same way; just replace “tangent” with either “sine” or “cosine.”
If we apply this to our example, we get \(x=\arctan \frac{7}{18}\).
Now, all we have to do is plug this into our calculator and then we have our answer! The inverse trig functions are typically found by hitting the 2nd key and then the trig function key. If we do this, we find that \(x\approx 21.25^{\circ}\).
Example #3
Let’s try another example. Use inverse trig functions to solve for \(x\).
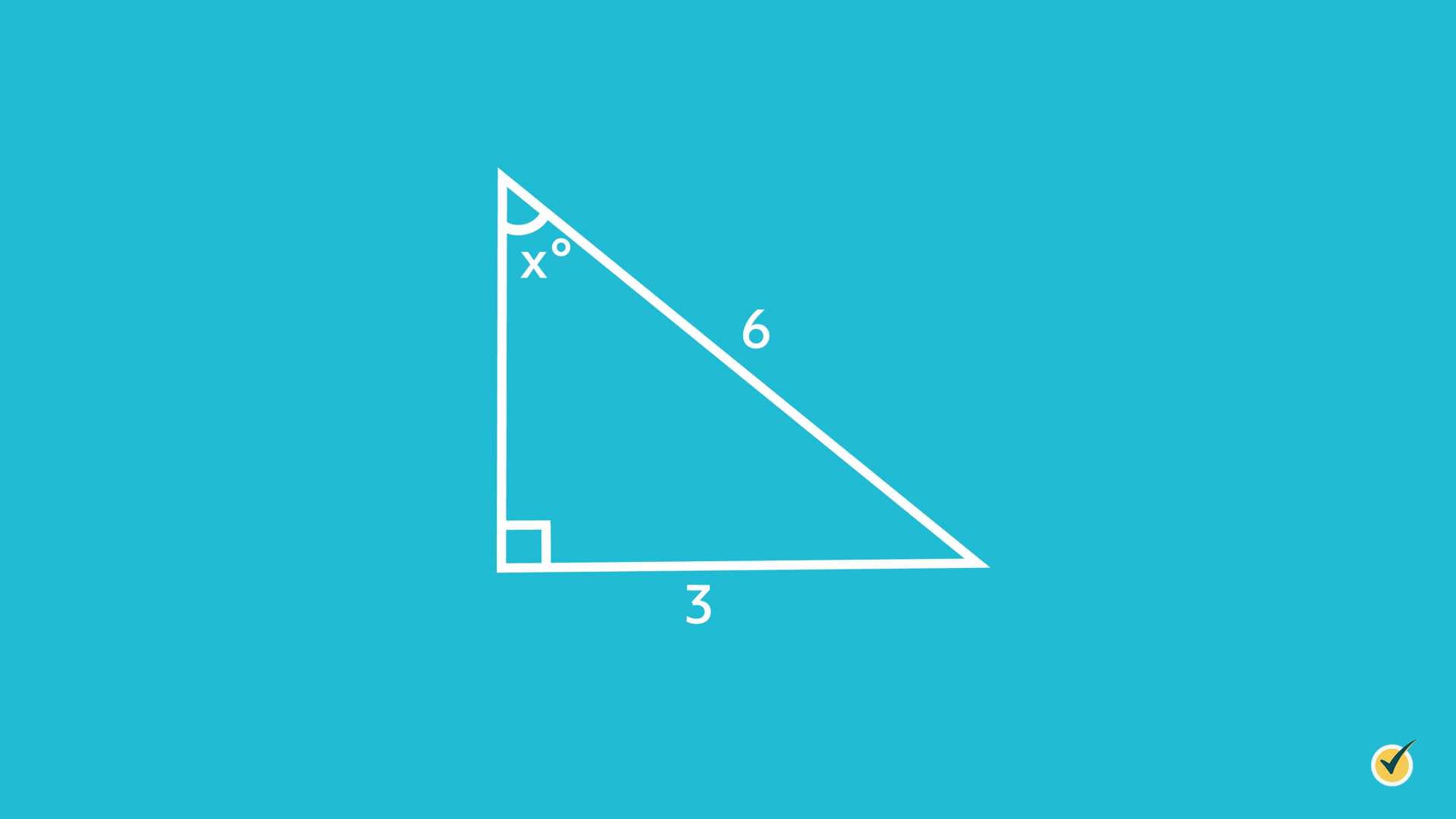
We are looking for our angle and we are given the opposite and hypotenuse side measures, so we are going to use SOH: \(\sin {x} =\frac{3}{6}\).
If we isolate \(x\) by itself, we get \(x=\sin^{-1}{\frac{3}{6}}\).
Remember, \(\text{asin }x\) and \(\sin^{-1}{x}\) mean the same thing, so the notation can be used interchangeably.
When we plug this into our calculator, we see that \(x=30^{\circ}\).
Example #4
I want you to try one more, but this time do it on your own. After I show you the problem, pause the video and work it out. Then when you finish, see if your answer matches up with mine.
Solve for \(x\).
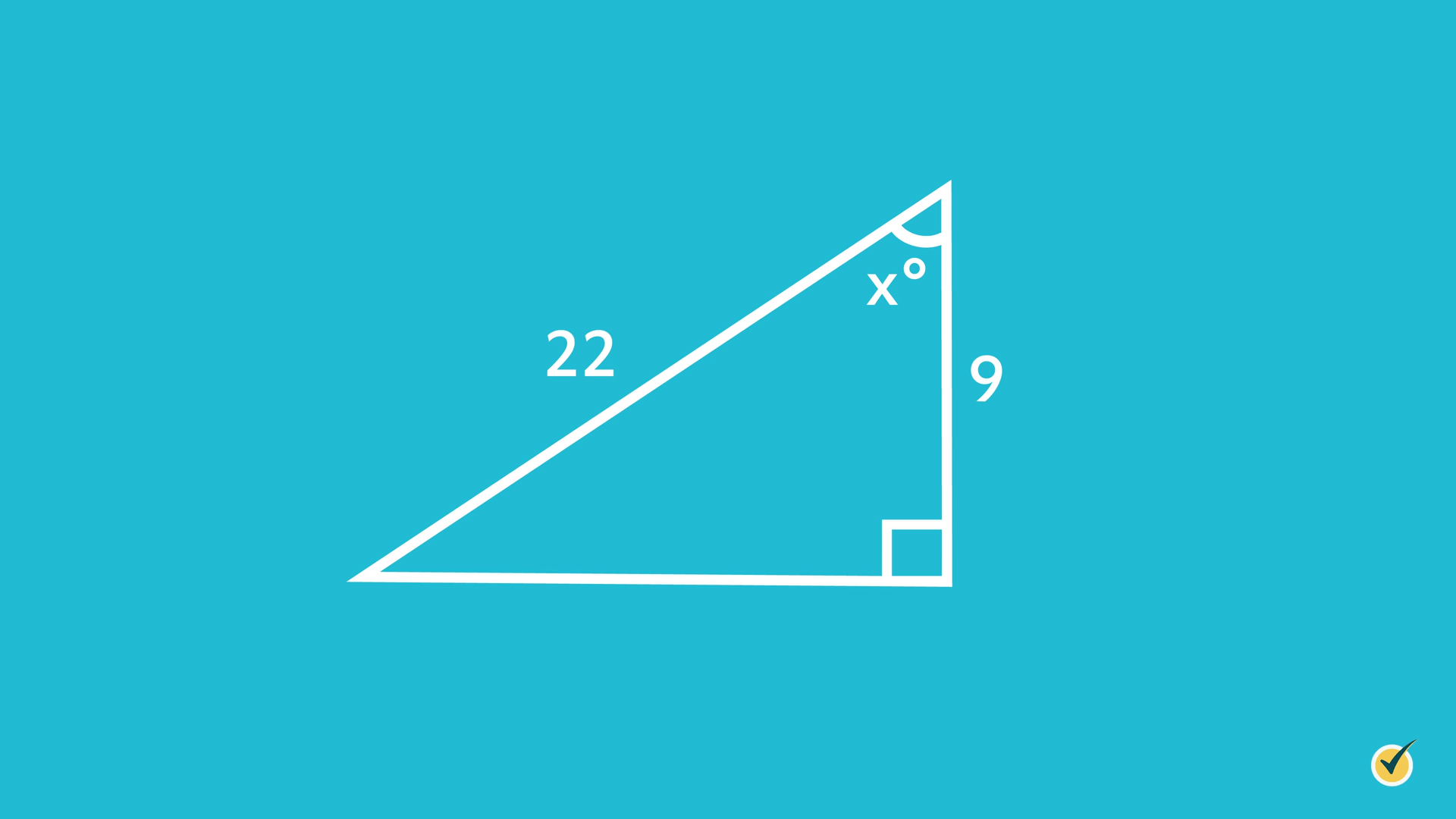
In this problem, we are given our adjacent and hypotenuse sides and we are looking for the angle between them. This means we are going to use CAH. If we set up our equation, it will look like this: \(\cos {x} =\frac{9}{22}\).
Solving for \(x\) by itself gives us \(x=\cos^{-1}\frac{9}{22}\).
When we plug this into our calculator, we get \(x\approx 65.85^{\circ}\).
Remember, inverse trig functions are just the opposite of trig functions. Trig functions are used to find the ratio of the sides of a triangle as related to the angle, and inverse trig functions help you figure out what that angle measure is when given the ratio of the sides.
I hope this review on inverse trig functions was helpful. Thanks for watching, and happy studying!
Inverse Trig Functions Practice Questions
Which item shows an incorrect way to express the inverse of a tangent trig function?
The inverse of a tangent trig function can be written as \(\text{arctan}x\), \(\text{atan}x\), or \(\text{tan}^{-1}x\). Inverse trig functions are used to calculate the angle measures of a right triangle, when the side measures are known.
What is the measure of angle \(x\)?
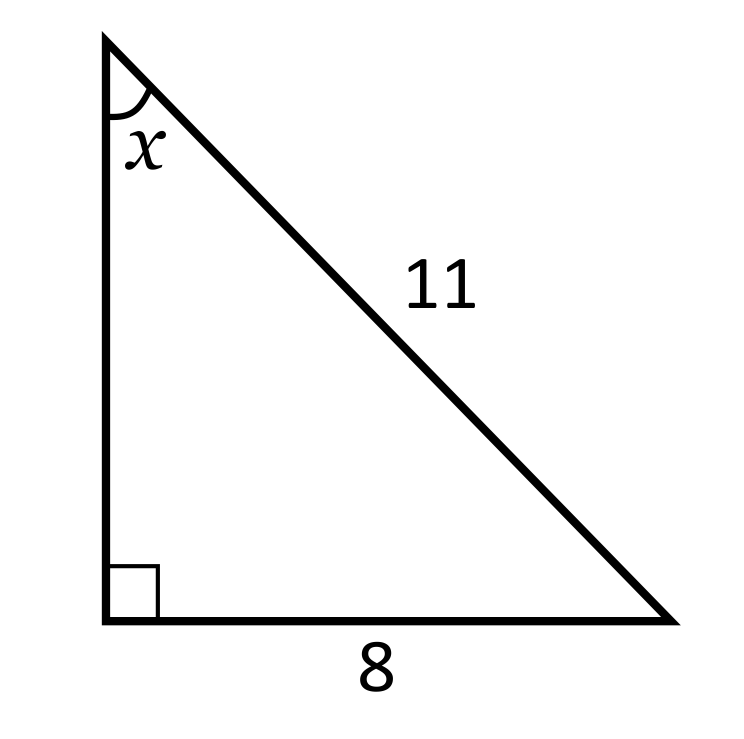
We know that the opposite side is \(8\), and the hypotenuse is \(11\). This means that SOH will be used, or the sine function. The sine function refers to “opposite over hypotenuse”, so when the equation is set up it will show \(8\) over \(11\). The equation starts as \(\text{sin}x=\frac{8}{11}\). In order to solve for \(x\), we need to use the inverse of this trig function. \(\text{sin}x=\frac{8}{11}\) becomes \(x=\text{sin}^{-1}\frac{8}{11}\), which simplifies to approximately \(46.7°\).
Will the following angle be found using sine, cosine, or tangent?
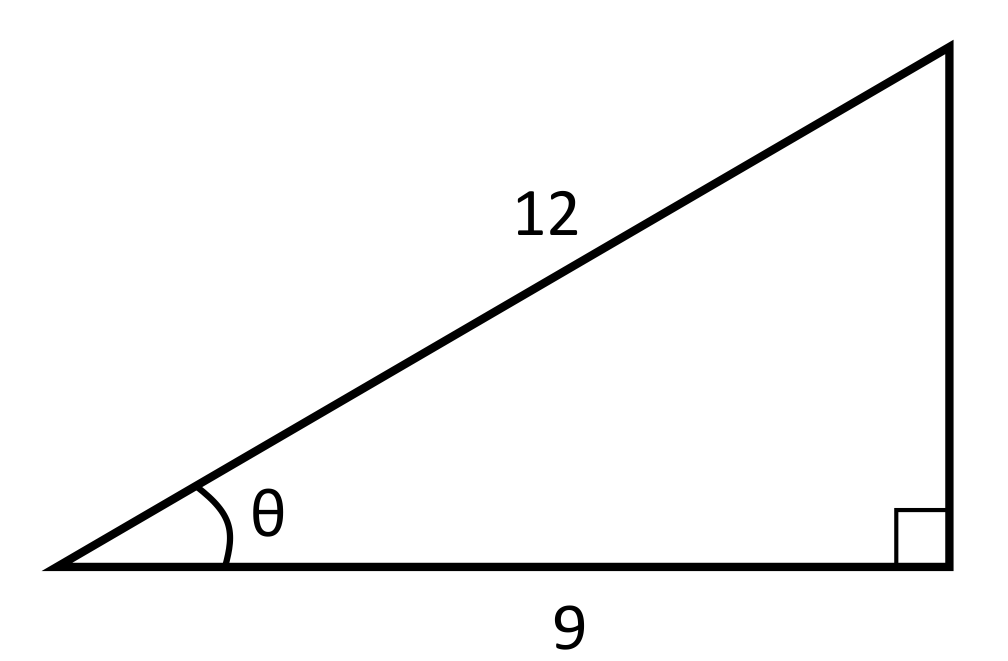
The unknown angle will be identified using the cosine trig function. The adjacent side length and the hypotenuse are provided, which means CAH, or cosine will be used. The angle would be identified using the equation \(x=\text{cos}^{-1}\frac{9}{12}\), which simplifies to \(41.4°\).
A tree that is \(51\) feet tall casts a shadow that is \(62\) feet long. What is the angle of elevation formed between the ground and the blue line?
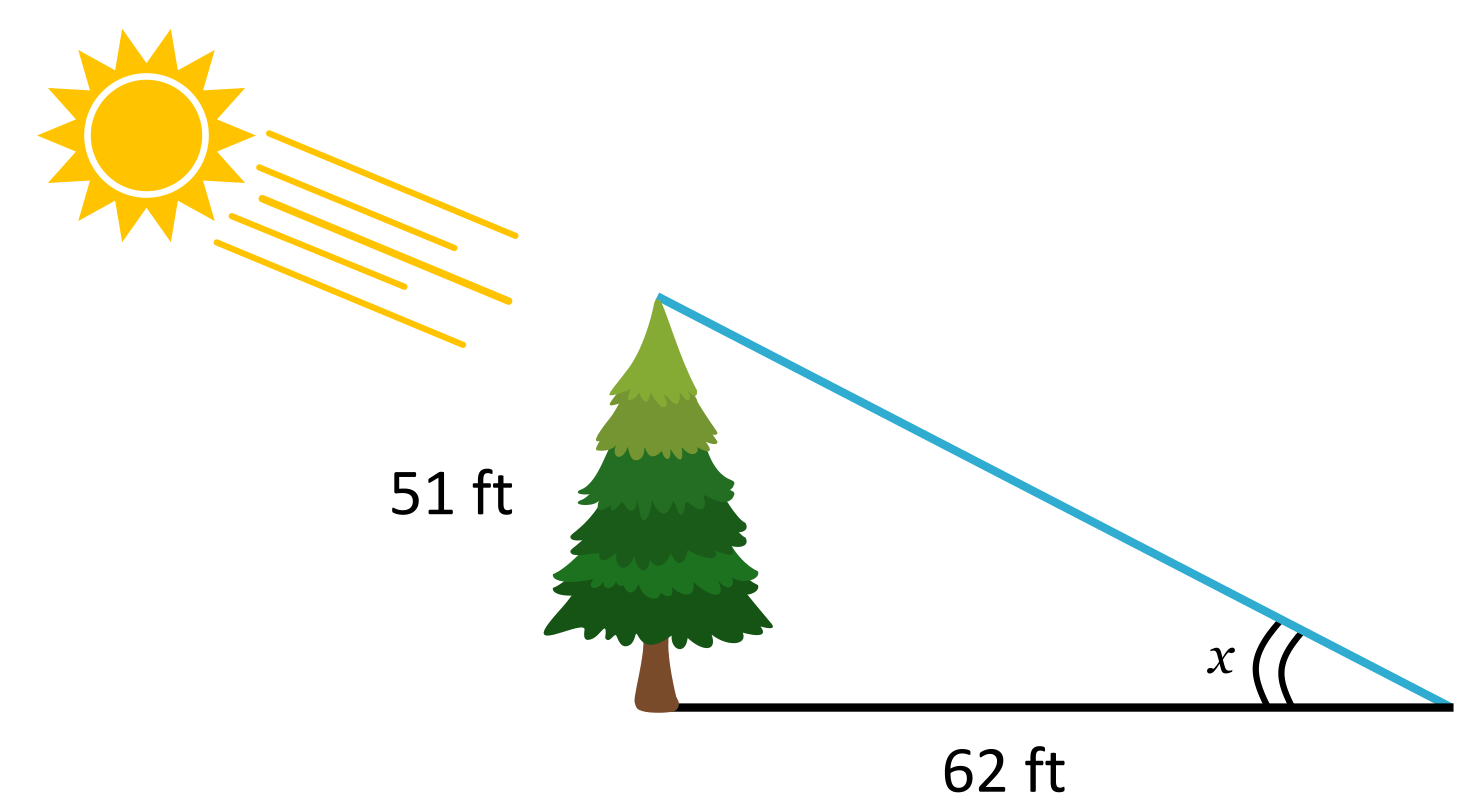
The opposite and adjacent side lengths are provided, so the TOA, or tangent function will be used. The equation will start out as \(\text{tan}x=\frac{51}{62}\), but in order to solve for \(x\) we will need to use the inverse of this trig function. \(\text{tan}x=\frac{51}{62}\) becomes \(x=\text{tan}^{-1}\frac{51}{62}\) which simplifies to \(x=39.4°\).
What is the angle created by the ladder and ground, in order for the ladder to reach the top of a ten-foot wall that is three feet from the base of the ladder?
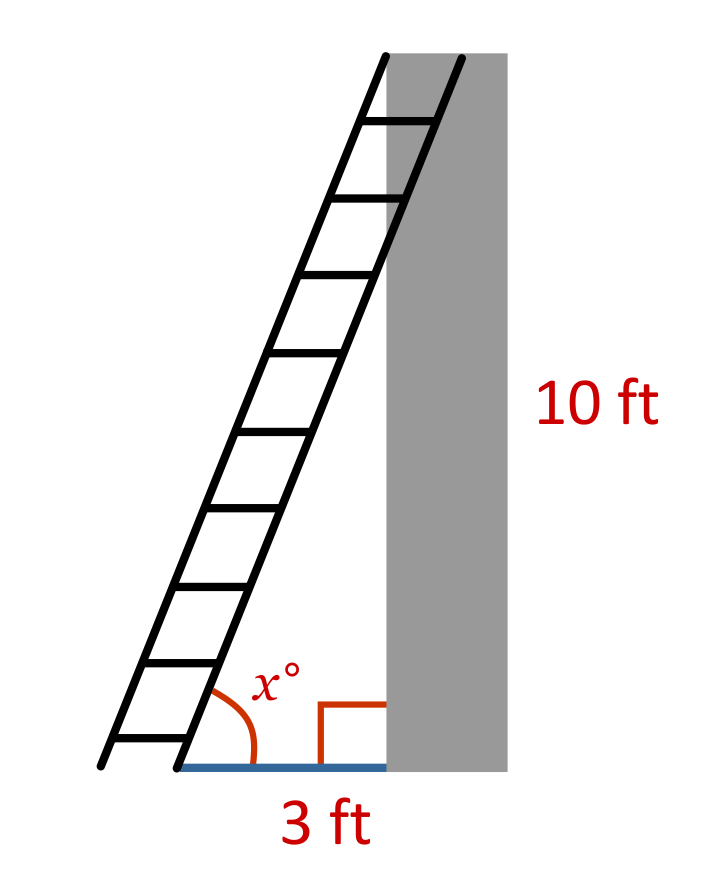
Angle \(x\) can be calculated using an inverse trig function. The side lengths that are opposite and adjacent to angle \(x\) are provided, which represents TOA, or the tangent function. The equation will start out as \(\text{tan}x=\frac{10}{3}\), and in order to solve for \(x\) we need to use the inverse of this trig function. \(\text{tan}x=\frac{10}{3}\) becomes \(x=\text{tan}^{-1}\frac{10}{3}\), which simplifies to \(x=73.3\). This means that the measure of angle \(x\) is \(73.3°\).