Inductive and Deductive Reasoning

Hi, and welcome to this video on inductive and deductive reasoning!

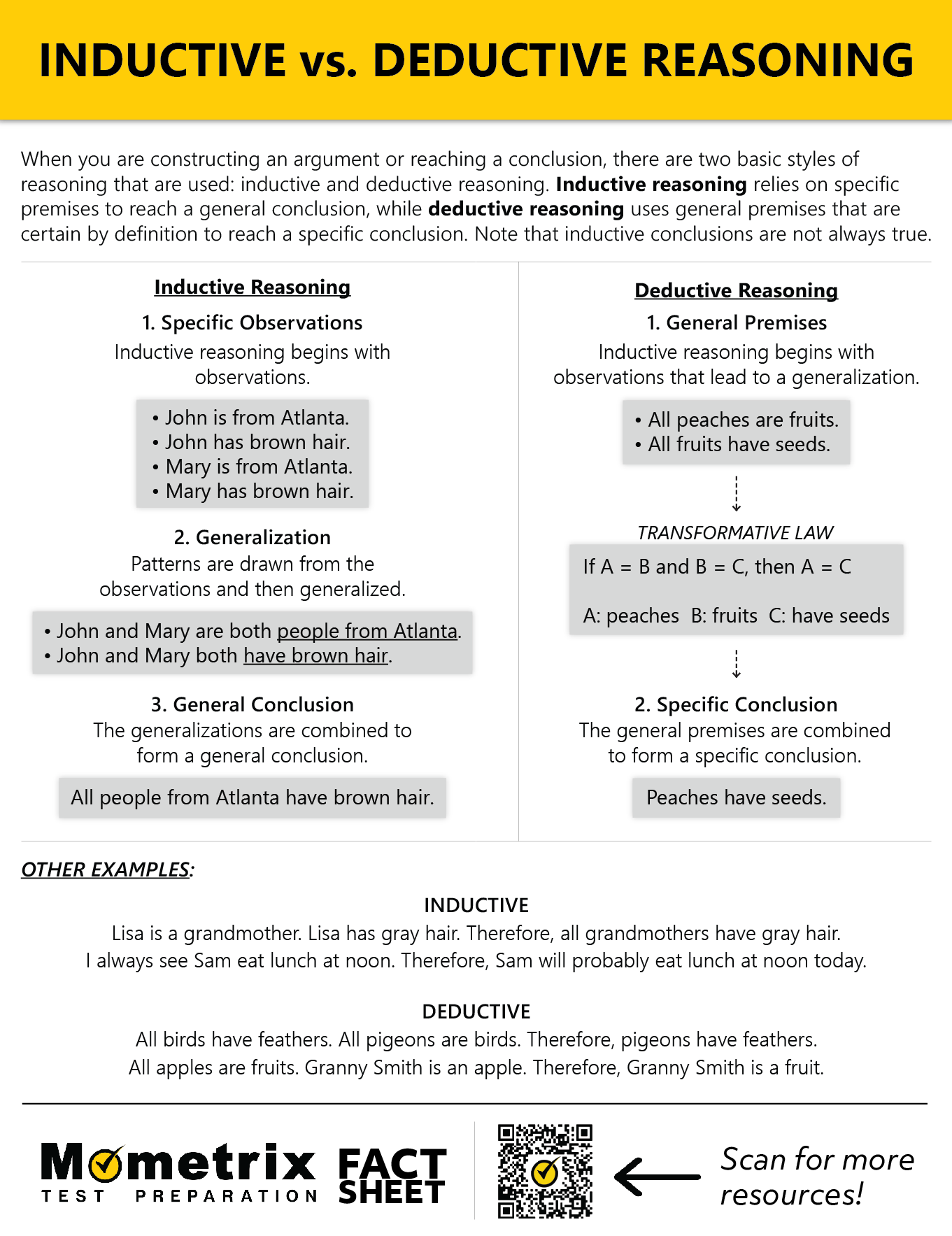
There are two basic styles of reasoning used to construct an argument or to reach a conclusion about the way things are inductive and deductive reasoning. Inductive reasoning relies on evidence and observation to reach a possible truth of the conclusion. We say possible truth because inductive conclusions are not certain, only probable. Deductive reasoning, on the other hand, uses statements, or premises, that are certain by definition.

Let’s start by looking at inductive reasoning.

Inductive Reasoning

When performing induction, we take a specific premise or set of premises and apply it to the world in a general way. In other words, we use a mass amount of specific examples in order to arrive at a general principle.

But what exactly does this mean in a practical sense? Let’s dig a little deeper and look at some real-world examples of inductive reasoning.

There are several historical examples showing that assumed truths derived from induction were later proven to be false. For example, all mammals were once assumed to be born living; this conclusion was reasonably justified based on pre-existing observational evidence: every known mammal was observed to be born living. However, after Europeans encountered the platypus in Australia and discovered that its young were hatched from eggs, this inductive conclusion was proven false. The platypus’ eggs negated the “truth” of all mammals being products of live birth.

Let’s suppose you roll a pair of dice 1,000 times and wind up with two 6s each time. It is reasonable to conclude, for instance, that the dice may be loaded. However, it is always possible that the next roll will be another combination of numbers, that the sequence of 6s was a mere statistical anomaly.

This goes for several otherworldly phenomena as well. We often, if not always, assume that the sun will rise each day. However, this is simply based on past experience and observation. There is always a chance that the sun will not rise tomorrow, that our understanding of the laws of nature is gravely flawed. In fact, scientific inquiry has already induced throughout observations of other stars in the universe that the sun will not only fail to rise one day but will also cease existing altogether. Here again, this line of induction may fail to be correct. Perhaps our sun is an anomaly; is it possible for the sun to last forever? It is quite unlikely based on our current understanding of solar behavior, but responsible induction never ignores that possibility.

Deductive Reasoning

Deductive reasoning proceeds in the opposite direction. Remember that induction proceeds from specific cases to reach a general principle. In a line of deductive reasoning, a general premise leads to a specific conclusion. Let’s look at a famous example:

All men are mortal. (premise)
Socrates was a man. (premise)
Therefore, Socrates was mortal. (conclusion)

 
Here the first premise makes a general claim about the nature of men, namely their mortality. From here, the conclusion is reached that Socrates is mortal because he falls within the category “man.” Hence, we see a move from a general premise to a specific conclusion. Assuming that the premises are true, then it necessarily follows that the conclusion is also true based on the form of the argument itself.

Let’s look at the concepts of validity and soundness. An argument is valid if it follows the correct format. For example, our previous example can be replaced with the following formula:

All A (men) are B (mortal).
C (Socrates) is A (man).
Therefore, C (Socrates) is B (mortal).

 
This type of logical argument is known as a syllogism. An essential factor here is that the conclusion follows logically from the premises. It is, by definition, valid.

But what about soundness? A line of reasoning is considered sound if the premises and the conclusion not only follow the proper format but are also themselves true. This may appear silly on the surface until we look at an example of an argument that follows the proper form (All A are B. > C is A = C is B.) but contains untrue premises. For instance:

All men are sheep.
Socrates was a man.
Therefore, Socrates was a sheep.

 
As we can see in this case, the correct form is being used, therefore making this example valid. However, it is patently untrue that Socrates was a sheep; therefore, the argument itself is unsound. Considering the validity and soundness of a deductive argument is important.

It is also important to remember that deduction is based on the form of the argument: general to particular, and so long as the premises are both valid and sound, the proceeding conclusion will also be true.

Now, to reiterate the major feature distinguishing induction from deduction:

• Induction uses specific observations to reach a reasonable (though uncertain) general principle.
• Deduction uses general premises that, if true, lead to a necessarily true conclusion about a specific instance.

Review

Before we go, here’s a review question to see what you’ve learned:

Which of the following statements is false?

1. Inductive reasoning starts with specific observations.
2. Conclusions reached from inductive reasoning are always true.
3. A deductive argument is sound if its premises are valid and true.
4. Conclusions reached from inductive reasoning have the potential to be falsified.

 
Thanks for watching, and happy studying!

• “Problem of Induction.” Wikipedia. Wikimedia Foundation. December 14, 2019.
• “Deductive Reasoning Examples.” n.d. Accessed May 31, 2023.

Frequently Asked Questions

Fact Sheet

Download Fact Sheet