Defined and Reciprocal Functions
Hi, and welcome to this video on reciprocal trig functions! Before we dive into what reciprocal trig functions are, let’s quickly review what normal trig functions are. The three most common trig functions are sine, cosine, and tangent. When given a right triangle, sine is the ratio of the triangle’s opposite to its hypotenuse, cosine is the ratio of its adjacent to its hypotenuse, and tangent is the ratio of its opposite to its adjacent. We remember these by using the phrase “SOH-CAH-TOA”.
When you take the reciprocal of an expression, you divide one by the expression. A super simple way of doing this is to turn your expression into a fraction and then flip it. So if our expression is 2, we would turn that into 2 over 1, which makes it easy to see that the reciprocal is one half. The reciprocal of three fifths is five thirds. And the reciprocal of 2x is 1 over 2x. With reciprocal trig functions, we have the same thing, except the reciprocals are given new names.
Let’s start with the reciprocal of sine, cosecant. Cosecant is the same as 1 over sine, or when you are given a triangle, the ratio of the triangle’s hypotenuse to its opposite. This is just the flipped version of SOH, sine equals opposite over hypotenuse.
Take a look at this example.
Given this triangle, what is the cosecant of theta? csc ϴ?
(see image at 1:20)
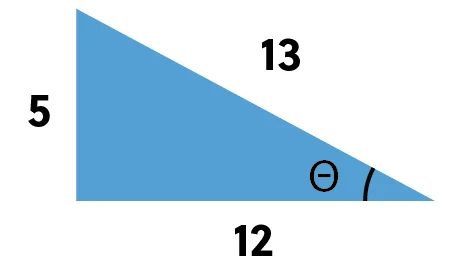
First, we need to remember that cosecant is the reciprocal of sine, so that means we need to figure out what sine is and flip it. Sine is opposite over hypotenuse, so in this case, 5 over 13. Then we flip that to get cosecant of theta, which is 13 over 5.
The second reciprocal function we are going to look at is secant, the reciprocal of cosine. Secant is the ratio of a triangle’s hypotenuse to its adjacent, or H over A, which, if you think back to our CAH from SOH-CAH-TOA is the flipped version of cosine equals A over H. Let’s try an example problem using secant.
Find the missing side using secant.
(see image at 2:01)
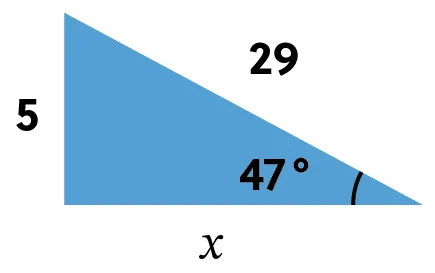
If we set up our equation, we get secant of 47 is equal to 29 over x
\(sec\:47 =\frac{29}{x} \\\)since our angle is measured 47 degrees and our hypotenuse is 29.
This can be rearranged so that x is by itself, which looks like this: x is equal to 29 over secant of 47.
When we plug this into our calculator, making sure our calculator is in degrees mode instead of radians, we get that x is approximately 19.78.
We have one more reciprocal function to cover and that is the reciprocal of tangent, which is cotangent. Cotangent is 1 over tangent, or the ratio of a triangle’s adjacent over its hypotenuse.
Using the things we have learned from our examples on cosecant and secant, I want to try another one, this time using cotangent.
Given this triangle, what is the cotangent of theta?
(see image at 2:58)
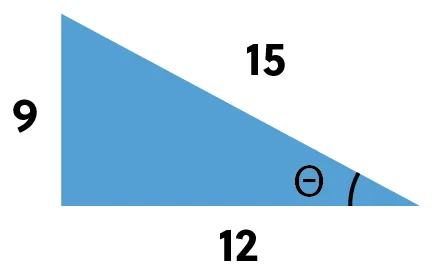
We know that tangent is opposite over adjacent, so since cotangent is the reciprocal of tangent, it must be the adjacent over opposite. This gives us the ratio, 12 over 9, so the cotangent of theta is 12 over 9.
Now that we have covered all the reciprocal trig functions, I want to mention something important about them. Reciprocal trig functions pop up all the time in homework or test problems, so it is important to recognize the names and recall what function they go to. However, as you may have noticed from our examples, when solving triangles by yourself, you almost always are able to use the original, or defined, trig function instead of its reciprocal. Most commonly you will only use sine, cosine, and tangent, but as I said, the reciprocal trig functions will come up on homework and tests occasionally, so it is very important to recognize them and understand what they mean even if you do not use them in your own personal application of trigonometry.
Before we end this video, I want to give you one more example to try on your own. Once I put it up, pause the video and see what answers you can come up with. Then you can check them with mine and see how you did.
Given this triangle, find the cosecant of theta, the secant of theta, and the cotangent of theta.
(see image at 4:10)
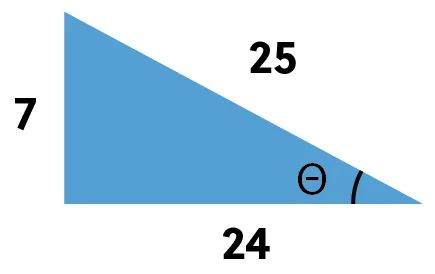
Remember, cosecant is the reciprocal of sine so we are looking for the hypotenuse over the opposite. The cosecant of theta is 25 over 7. Secant is the reciprocal of cosine, so we need the hypotenuse over the adjacent, which gives us that secant of theta is equal to 25 over 24. And finally, cotangent is the reciprocal of tangent so we need the adjacent over the opposite, which leaves us with cotangent of theta is 24 over 7.
I hope this review of reciprocal trig functions was helpful. Thanks for watching and happy studying!
Defined and Reciprocal Function Practice Questions
Which of the following ratios describes the secant function, abbreviated sec(θ)?
The secant function is the reciprocal of the cosine function, and \(\text{cos}=\frac{\text{adj}}{\text{hyp}}\), which we can recall easily from SOH-CAH-TOA. To take the reciprocal, we simply flip this fraction to get the solution, \(\text{sec}=\frac{\text{hyp}}{\text{adj}}\).
Which of the following is the correct ratio for the cosecant function, csc(θ)?
Cosecant is the reciprocal of the sine function. Now, recall that \(sin(θ)=\frac{\text{opp}}{\text{hyp}}\) (“SOH”). To find the ratio for csc(θ), we simply need to flip the sine ratio, which will give us \(\frac{\text{hyp}}{\text{opp}}\).
Observe the triangle below and calculate the value of cot(θ).
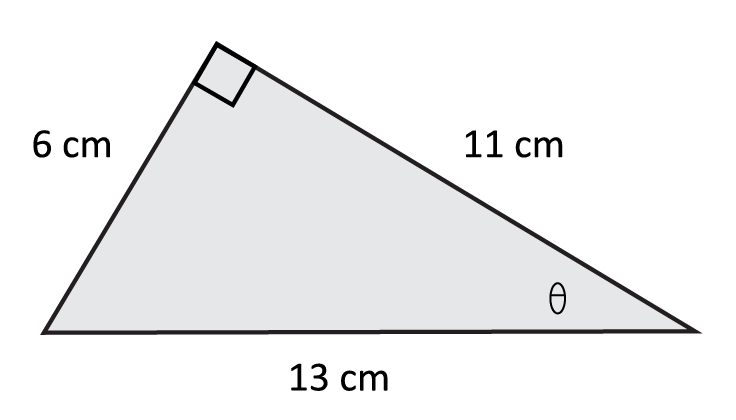
The cotangent function is the reciprocal of the tangent, so instead of opposite over adjacent (“TOA”), we will take adjacent over opposite. The length of the triangle side next to (adjacent to) θ is 11 cm, while the length across from θ (opposite) is 6 cm. Therefore, our solution is \(\frac{11}{6}≈1.833\).
Observe the following triangle, and use the secant function to determine side length s.
2.75 in
3.6 in
4.25 in
3.97 in
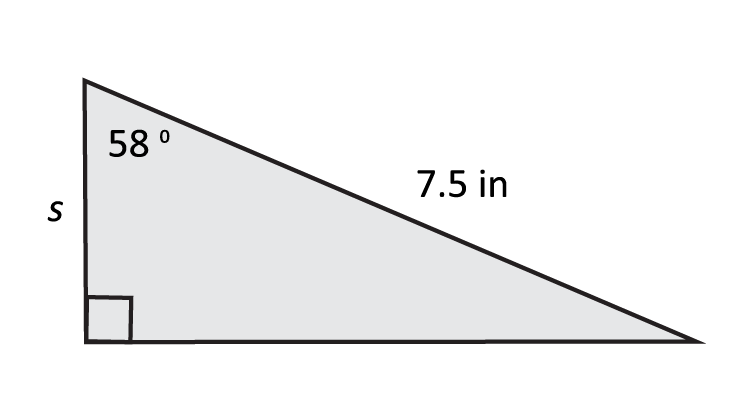
Once again, \(\text{sec}(θ)=\frac{\text{hyp}}{\text{adj}}\). Even though we are only given the length of one side, we can solve for the adjacent side length using a little algebra. Simply plug in the values of θ and hyp as follows:
\(\text{sec}(58°)=\frac{7.5}{s}\)
Rearranging, we can get s by itself:
\(s=\frac{7.5}{\text{sec}(58°)}\)
Using a calculator, we can determine that \(\text{sec}(58°)≈1.887\). From here, \(s=\frac{7.5}{1.887…}≈3.97\text{ in}\)
The value of the sine function evaluated at \(\frac{π}{3}\) radians is \(\text{sin}(\frac{π}{3})=\frac{\sqrt{3}}{2}\). Determine the value for \(\text{csc}(\frac{π}{3})\), in radians.
Recall that throughout this lesson, we have been referring to sec, csc, and cot as reciprocal functions. Of course, we have been jumping straight to thinking of cosecant as the ratio \(\frac{\text{hyp}}{\text{opp}}\). However, for this example we are not given side length information, so we need to examine the problem from a different perspective. Consider again the nature of reciprocals: in the same way that \(\frac{1}{x}\) is the reciprocal of \(\frac{x}{1}\), the reciprocal of sin(θ) is \(\frac{1}{\text{sin}(θ)}\). This fraction is equivalent to cosecant!
\(\frac{1}{x}\) is the reciprocal of \(\frac{x}{1}\)
\(\frac{1}{\text{sin}(θ)}\) is the reciprocal of sin(θ)
Since csc is the reciprocal of sin, \(\text{csc}(θ)=\frac{1}{\text{sin}(θ)}\)
Now, all we need to do to calculate \(\text{csc}(\frac{\pi}{3})\) is divide 1 by \(\text{sin}(\frac{\pi}{3})\). Since we were given the value of \(\text{sin}(\frac{\pi}{3})\), \(\frac{\sqrt{3}}{2}\), we can get the solution by flipping it, then rationalizing the denominator.
\(\frac{2}{\sqrt{3}}\) is the reciprocal of \(\frac{\sqrt{3}}{2}\)
\(\frac{2}{\sqrt{3}}\times\frac{\sqrt{3}}{3}=\frac{2\sqrt{3}}{3}\)
The solution can also be attained by entering \(1\div\text{sin}(\frac{\pi}{3})\) into your calculator.
\(1\div\text{sin}(\frac{\pi}{3})=\frac{2\sqrt{3}}{3}\)