
Hi, and welcome to this review of the unit circle! In this video, we will go over what the unit circle is and what it is used for.
Degrees vs. Radians
Before we get into the unit circle itself, let’s talk about degrees and radians. Most of the time, when you measure an angle, you measure it in degrees. For instance, a right angle has 90 degrees, a straight angle has 180 degrees, and there’s an angle for every number in between.
But there’s actually another way you can measure an angle, and that’s by measuring in radians. Measuring in radians relates the angle to \(\pi \), so \(\pi \) will be in almost every angle measure when measuring in radians.
Since \(\pi \) is the ratio of a circle’s circumference to its diameter, it makes sense that we use radians most often when working with circles.
As most of you have heard before, a circle has 360 degrees. It also has \(2\pi \) radians. Think of radians and degrees like centimeters and inches. They are two different forms of measurement but they can be used to measure the same thing and can be converted between.
How to Convert Between Degrees and Radians
The conversion used for radians and degrees is \(2\pi \text{ rad}=360^{\circ}\), or if you simplify that, \(\pi \text{ rad}=180^{\circ}\). Let’s say we want to convert \(270°\) to radians. We’re going to take our \(270°\) and multiply by our conversion factor, which is \(\frac{\pi \text{ rad}}{180^{\circ}}\). This then simplifies to \(\frac{3\pi }{2}\text { rad}\).
Now let’s try an example converting from radians to degrees. Let’s look at \(\frac{\pi }{6}\text{ rad}\). If we multiply this by our conversion factor, we’re going to multiply this time by \(\frac{180^{\circ}}{\pi \text{ rad}}\), which then simplifies to \(30°\).
Now let’s look at how this relates to the unit circle.
What is a Unit Circle?
A unit circle is a circle which has a radius of one unit and its center is at the origin. This may seem fairly common and you might be getting excited if you think I’m going to ask you to find the circumference or area. With a radius of one, that wouldn’t be very difficult. But today we are going to look at this circle through the lens of trigonometry.
Trigonometry is the study of how a triangle’s sides and angles relate to one another. Now, you’re probably wondering what circles and triangles have to do with one another and that’s a great question! One of the most common uses of trigonometry is in finding the measures of an angle given two sides of a right triangle. If we look closely at our circle, we can actually find right triangles in it. Here is an example:
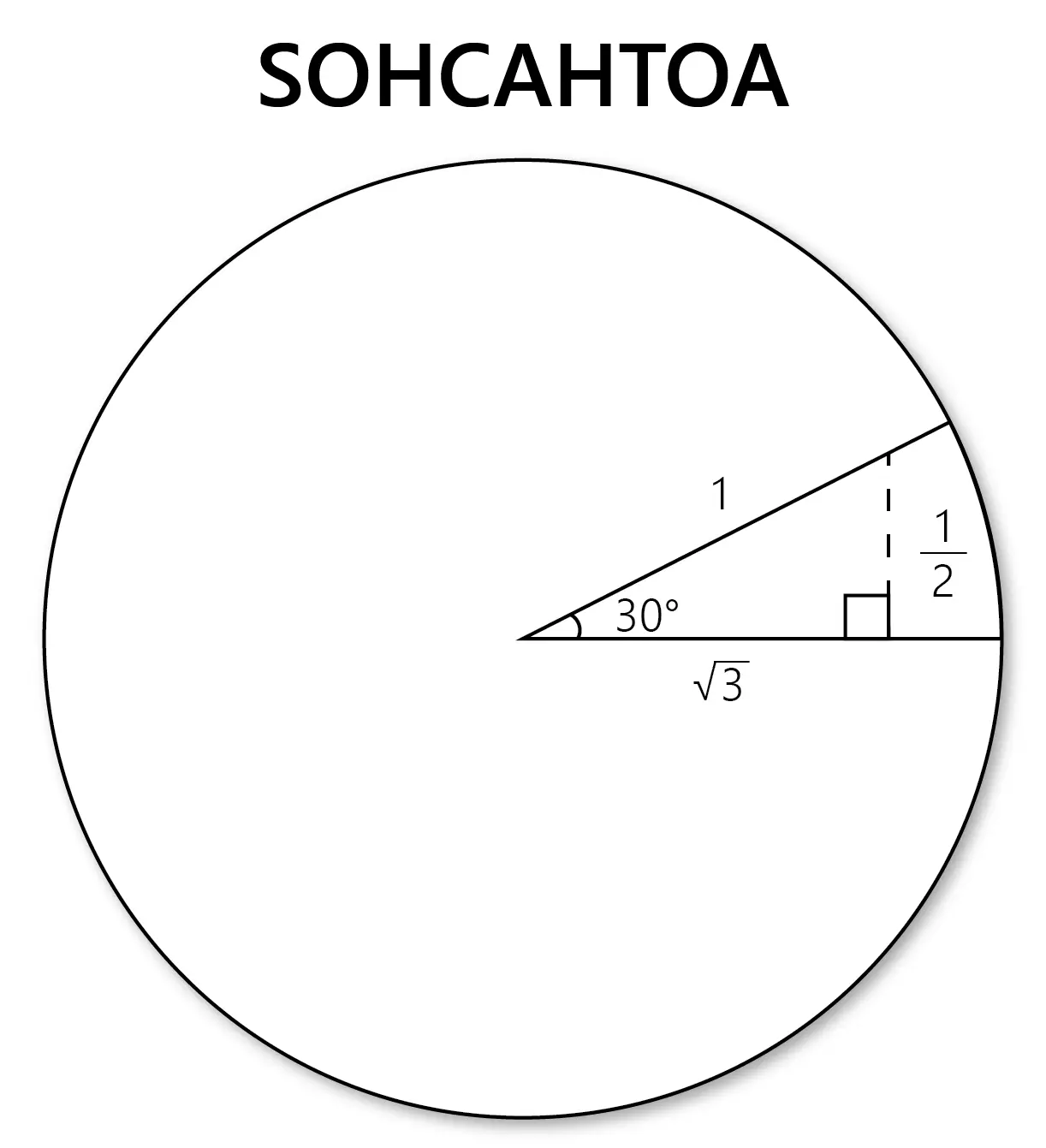
We know the radius is 1 and we can use SOHCAHTOA to find that the opposite is \(\frac{1}{2}\) and the adjacent side is \(\sqrt{3}\).
Trig Values
The unit circle is a collection of the most common right triangles, so we use it to remember the trig values of the most common angles. The coordinate points where the measure of a specific angle hits the circle gives us our sine and cosine values. For example, with a ray coming from the angle \(60°\), the point that ray hits the unit circle is at \((\frac{1}{2},\frac{\sqrt{3}}{2})\). The \(x\)-coordinate gives us our cosine value for that angle, and the \(y\)-coordinate gives us our sine value.
If you need to find the tangent value, simply put sine over cosine, or the \(y\)-coordinate over the \(x\)-coordinate. Going back to our example of \(60°\), \(\sin{60^{\circ}}=\frac{\sqrt{3}}{2}\), our \(y\)-coordinate, \(\cos{60^{\circ}}=\frac{1}{2}\), our \(x\)-coordinate, and \(\tan{60^{\circ}}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\), which simplifies to \(\sqrt{3}\).
Standard Position
An important thing to note when discussing these angle measures is that the angles must be in standard position. Standard position simply means that the vertex of the angle is at the origin of the circle and that one ray of the angle is on the positive \(x\)-axis. The other ray of the angle is placed at the angle measure formed by traveling counter-clockwise along the circle.
If an angle is not in standard position, it is important to place it in standard position before using the points to find your trig values.
Unit Circle Problem
I want you to try to find a couple of trig values on your own using the unit circle. For now, we will put it on the screen so you can refer back to it, but eventually, you may want to memorize it since these values come up frequently in mathematics.
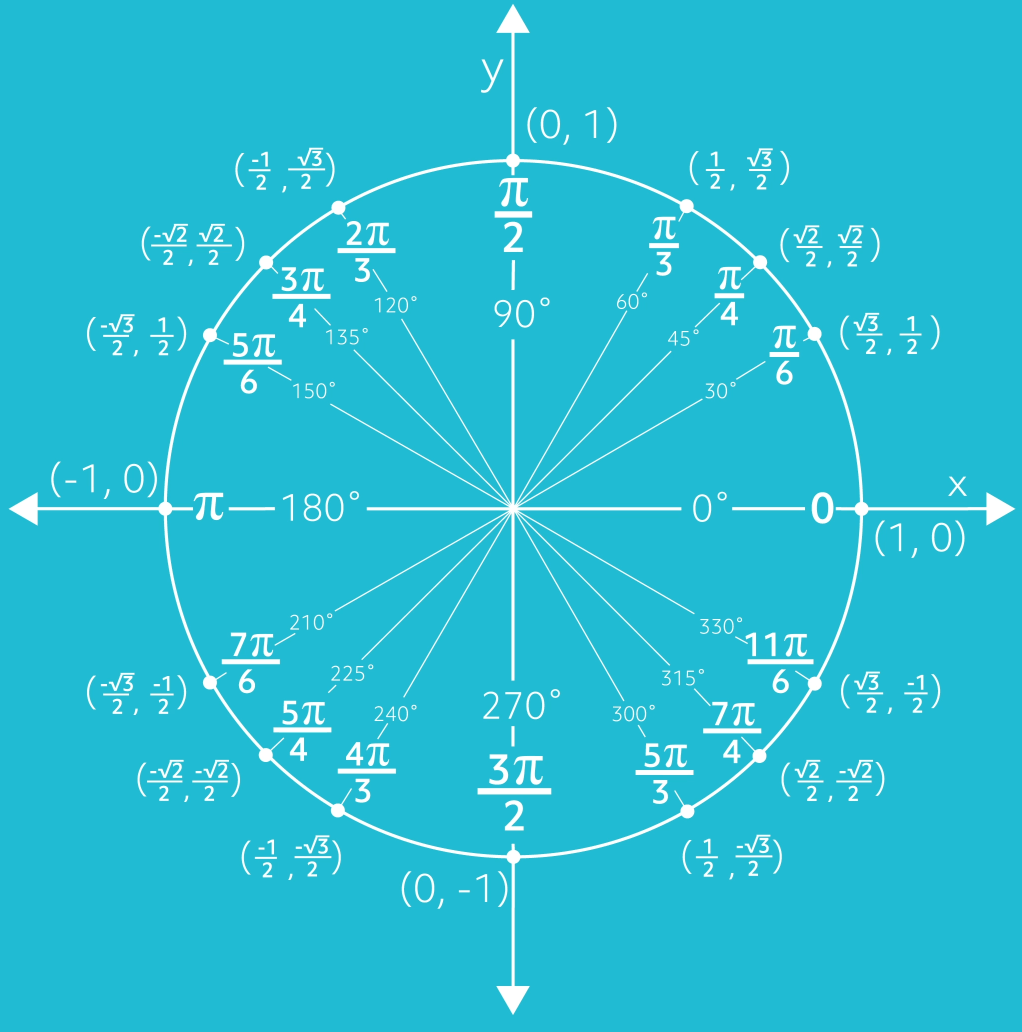
- \(\cos{180^{\circ}}\)
- \(\sin{\frac{2\pi }{3}}\)
- \(\tan{\frac{\pi }{4}}\)
Go ahead and pause the video and see what you can come up with.
Let’s check your answers. The \(\cos{180^{\circ}}=-1\), because at \(180°\), the ray hits the circle at the point \((-1,0)\). The \(\sin{\frac{2\pi }{3}}=\frac{\sqrt{3}}{2}\), because it hits at the point\((-\frac{1}{2},\frac{\sqrt{3}}{2})\). And the \(\tan{\frac{\pi }{4}}=1\) because the ray hits the circle at the point \((\sqrt{2},\sqrt{2})\). And \(\frac{\sqrt{2}}{\sqrt{2}}=1\). Remember, you can convert between radians and degrees using the conversion, \(\pi \text{ rad}=180^{\circ}\). We then use our unit circle, with angles in standard position, to find the trig values of common angle measurements.
I hope this review was helpful. Thanks for watching and happy studying!
Unit Circle Practice Problems
What is the value of cos 90° ? Use the Unit Circle.
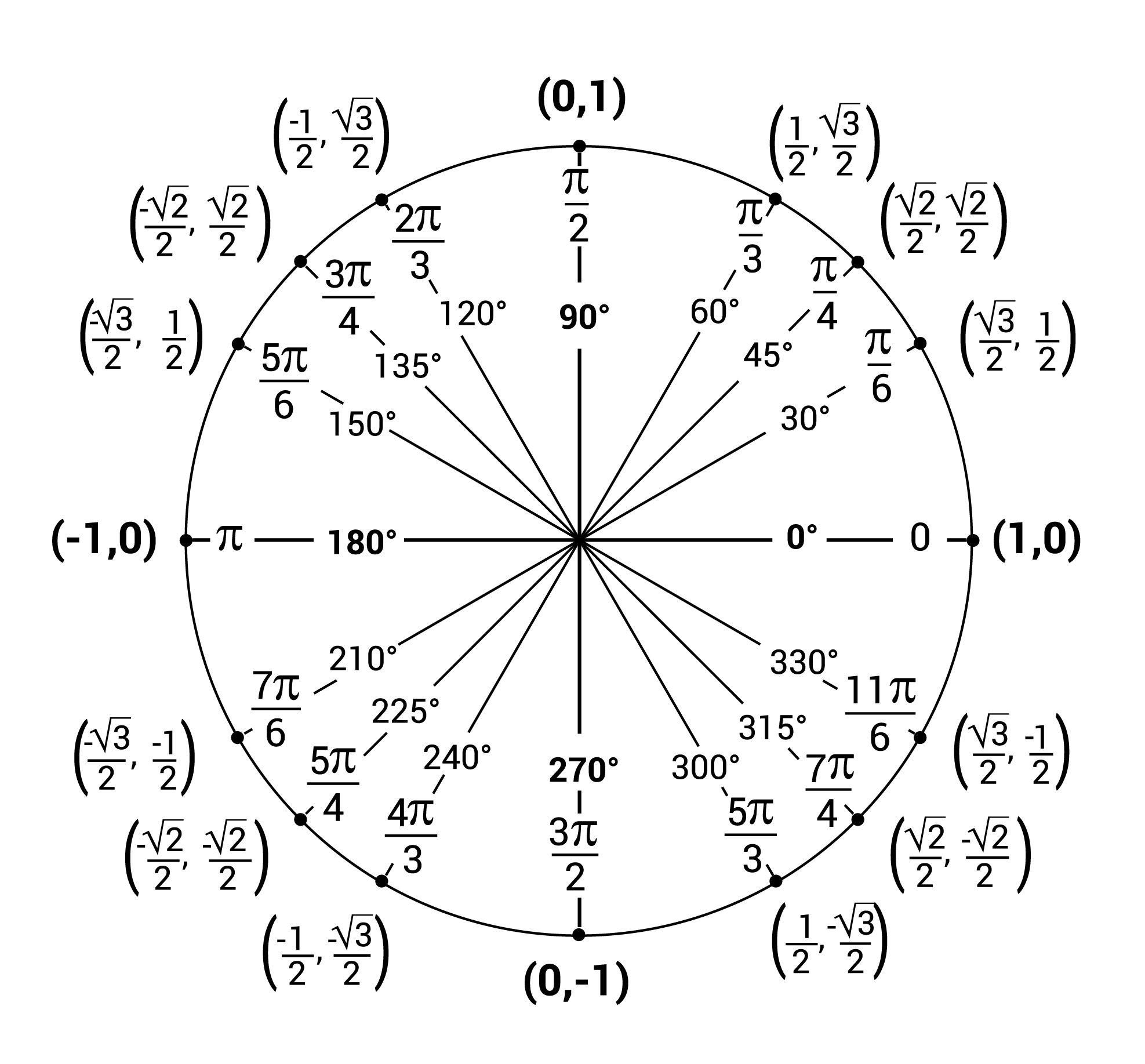
In a pair of coordinates \((x,y)\) on the unit circle, the coordinate x is the cosine of the angle formed by the point, the origin, and the x-axis.
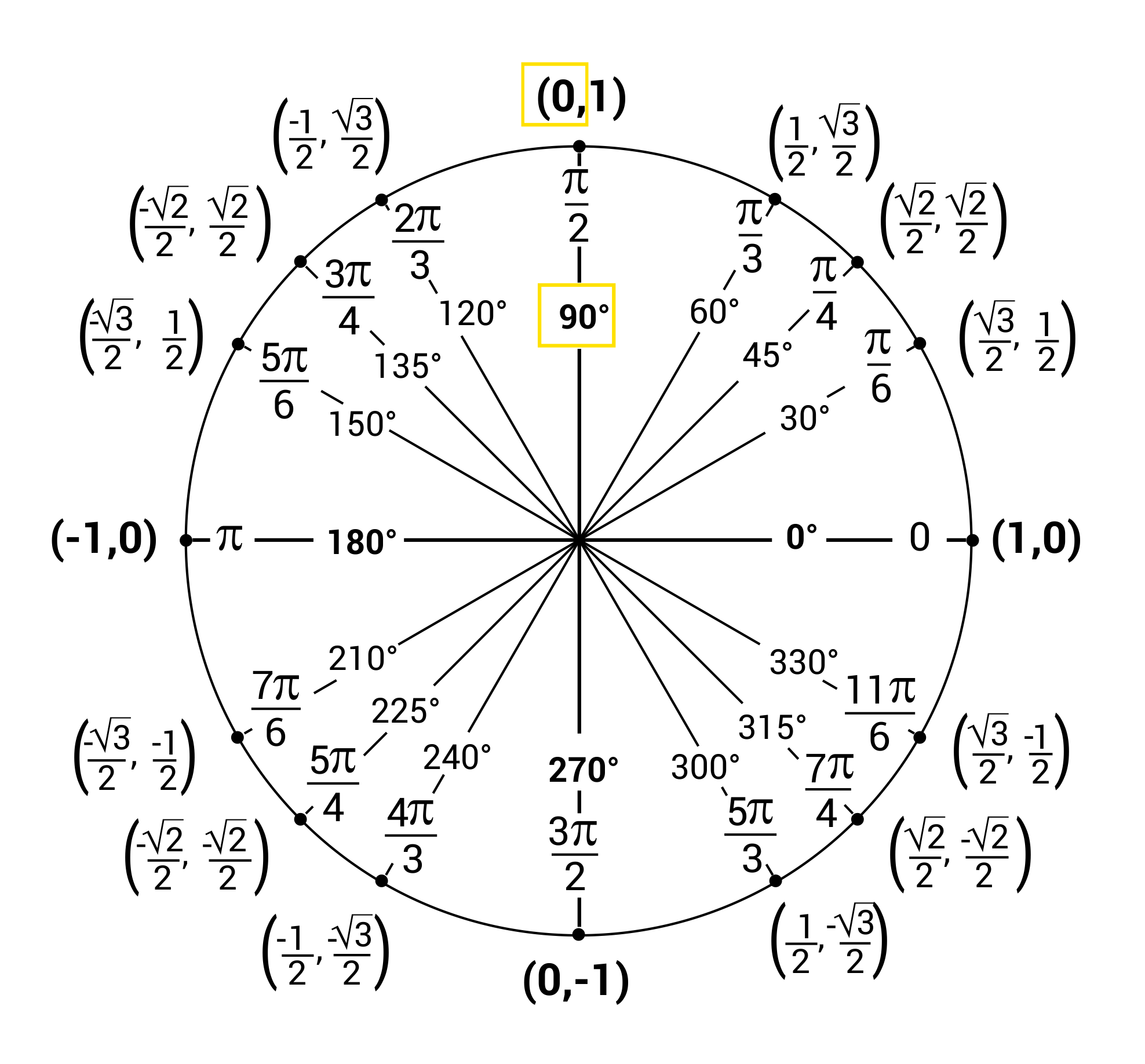
What is the value of sin \(\frac{3π}{4}\)? Use the Unit Circle.

In a pair of coordinates \((x,y)\) on the unit circle, the coordinate y is the sine of the angle formed by the point, the origin, and the x-axis.
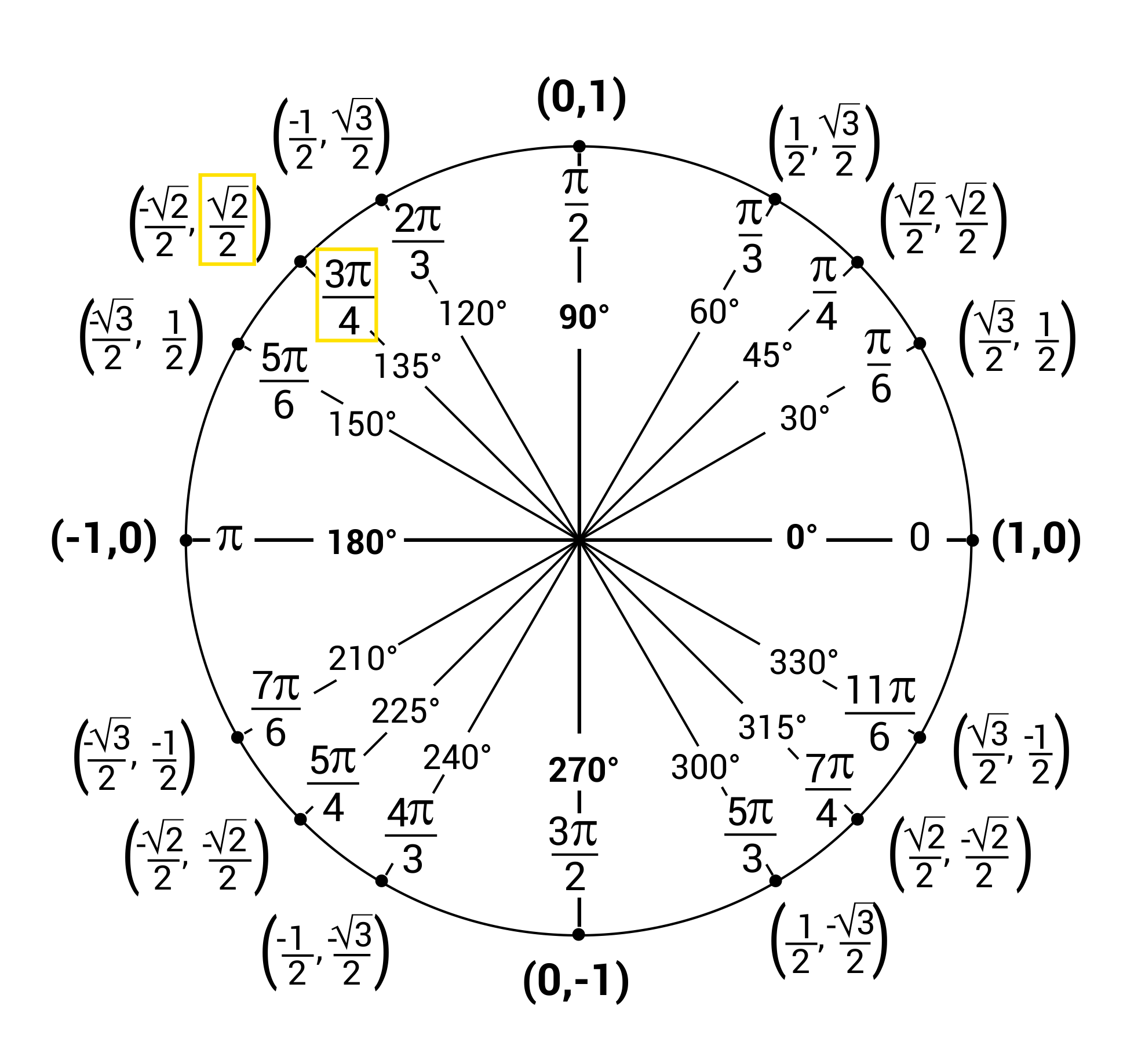
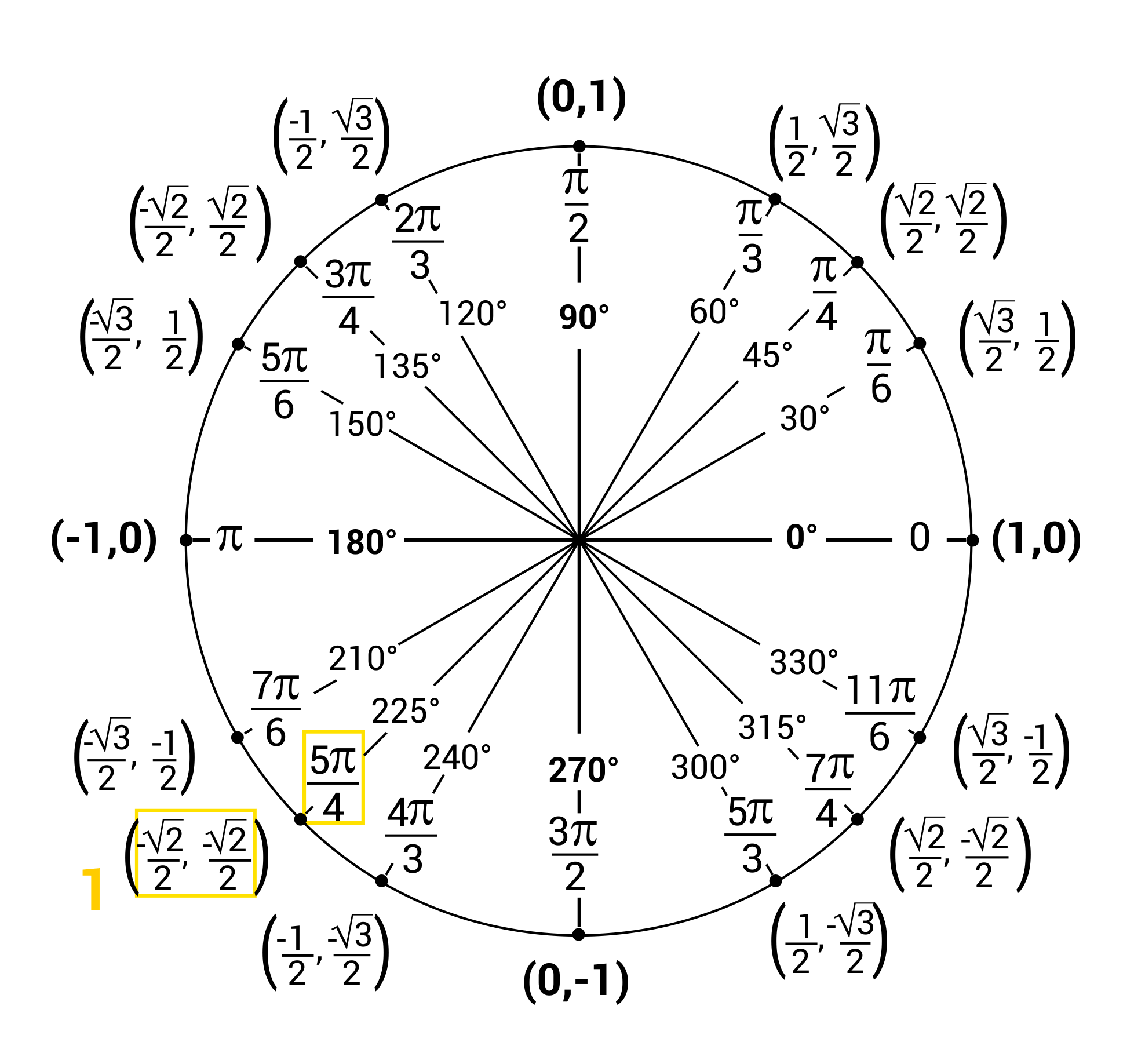
What is the value of tan \(\frac{5π}{4}\)? Use the Unit Circle.

The tangent function is found by dividing the y-value by the x-value.
\(-\frac{\sqrt{2}}{2}\div-\frac{\sqrt{2}}{2}=1\), so tan \(\frac{5π}{4}=1\)
180 degrees = ______________ radians.

We can solve this by multiplying 180 degrees by the conversion factor \(\frac{π\text{ rad}}{180\text{ degrees}}\). This simplifies to π rad.
\(\frac{5π}{3}\) rad = __________ degrees.

This can be solved by multiplying \(\frac{5π}{3}\) by the conversion factor \(\)\frac{180\text{ degrees}}{π}. This simplifies to 300 degrees.
The tangent of which two angles is \(\frac{\sqrt{3}}{3}\)?
The tangent of an angle is the ratio of \(\frac{\text{sin}}{\text{cos}}\). We know that the x– and y-coordinates of the points on the unit circle represent cosine and sine of the angle, respectively. We will look for the coordinates where the ratio of \(\frac{y}{x}=\frac{\sqrt{3}}{3}\). The x– and y-coordinates for the angles 30° and 210° simplify to \(\frac{\sqrt{3}}{3}\).
What is the cosine of \(\frac{4π}{3}\)?
We know that the x-coordinates of a point on the unit circle represent cosine. Locate \(\frac{4π}{3}\), which is equivalent to 240° at the coordinate \((-\frac{1}{2},-\frac{\sqrt{3}}{2})\). The x-coordinate of the point is \(-\frac{1}{2}\) and the cosine of \(\frac{4π}{3}\).
The \(\text{sin }Ɵ=\frac{1}{2}\), where 0° < Ɵ < 90°. What is the value of Ɵ in radians?
Since we are told that the value of Ɵ is in the first quadrant and we know that the y-coordinate of a point on the unit circle represents sine, we can look for a point on the unit circle where the y-coordinate is \(\frac{1}{2}\). The only point in the first quadrant with y-coordinate \(\frac{1}{2}\) is the point that represents angle 30° which is \(\frac{π}{6}\) in radians.