A vertical asymptote is an area of a graph where the function is undefined. A graphed line will bend and curve to avoid this region of the graph. Vertical asymptotes are vertical lines that correspond to the zeroes of the denominator in a function. A fraction cannot have zero in the denominator, therefore this region will not be graphed.
Determining vertical asymptotes goes hand-in-hand with determining the domain of a function. The domain of a function is all of the values of \(x\) that produce a non-zero denominator. The values that create a zero in the denominator will be the vertical asymptotes, or areas that the graphed line avoids.
For example, in the function \(f(x)=\frac{4}{9+x}\), the domain is determined by setting the denominator equal to zero, and then solving for the variable. \(9+x=0\) simplifies to \(x=-9\). This means that the domain is \(x-9\). The lines of this graphed function will not cross \(x=-9\), therefore the vertical asymptote is \(x=-9\). The line can come close to \(x=-9\), but it will ultimately bend to avoid crossing it.
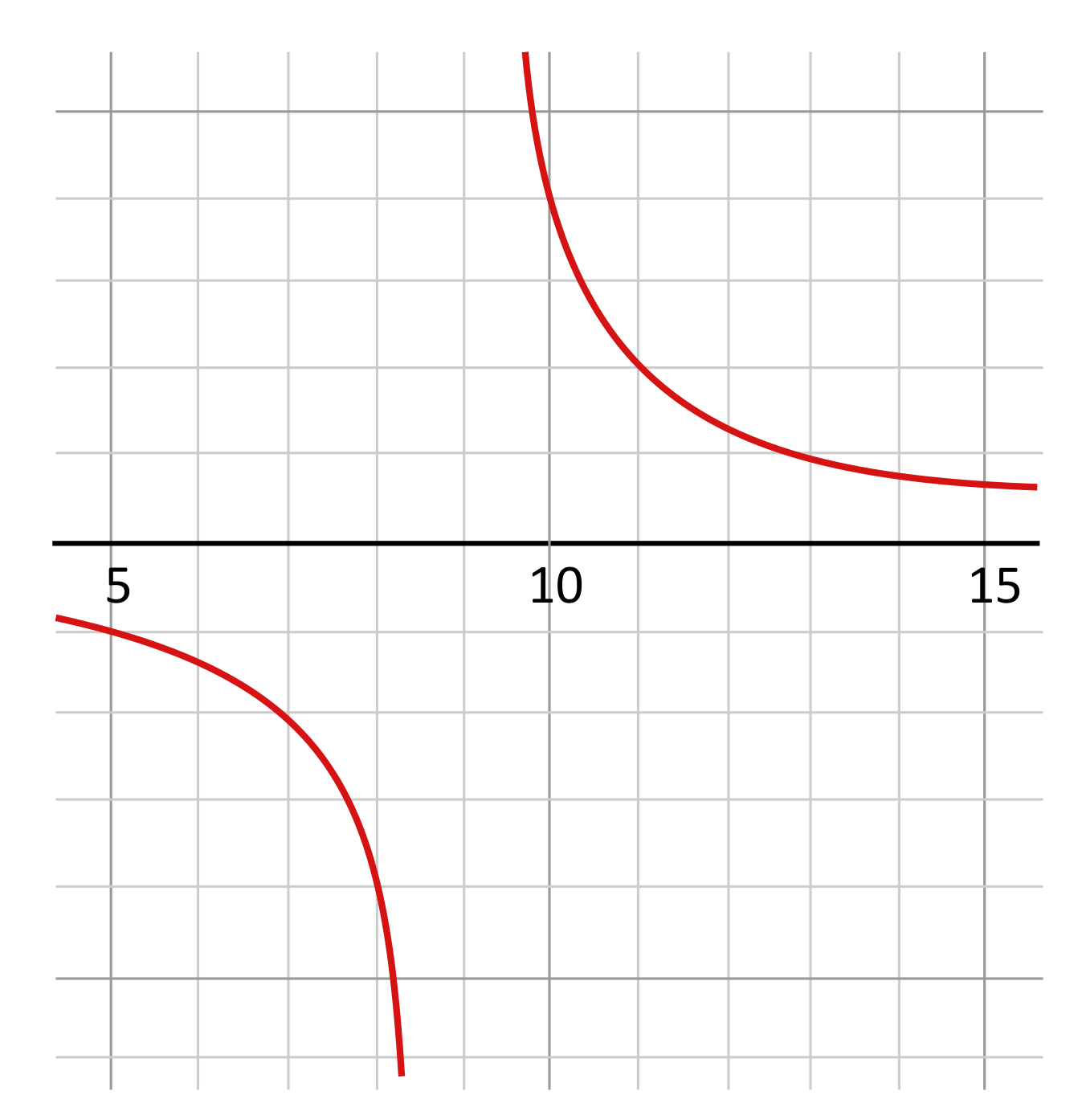
The domain of some functions will not be quite as obvious as \(\frac{4}{9+x}\). The denominator of some functions will need to be factored before the domain can be identified. For example, the domain of the function \(f(x)=\frac{x+2}{x^2+2x-8}\) is not obvious until the denominator is factored. \(x^2+2x-8\) becomes \((x+4)(x-2)\) when factored.
Now each set of parentheses can be set equal to zero in order to identify the domain of the function. \(x+4=0\) simplifies to \(x=-4\), so \(x\) cannot be \(-4\). \(x-2=0\) simplifies to \(x=2\), so \(x\) cannot be \(2\). \(x\) cannot be \(-4\) or \(2\) because this creates a zero in the denominator. This also means that the vertical asymptotes of the function \(f(x)=\frac{x+2}{x^2+2x-8}\) are \(x=-4\) and \(x=2\).
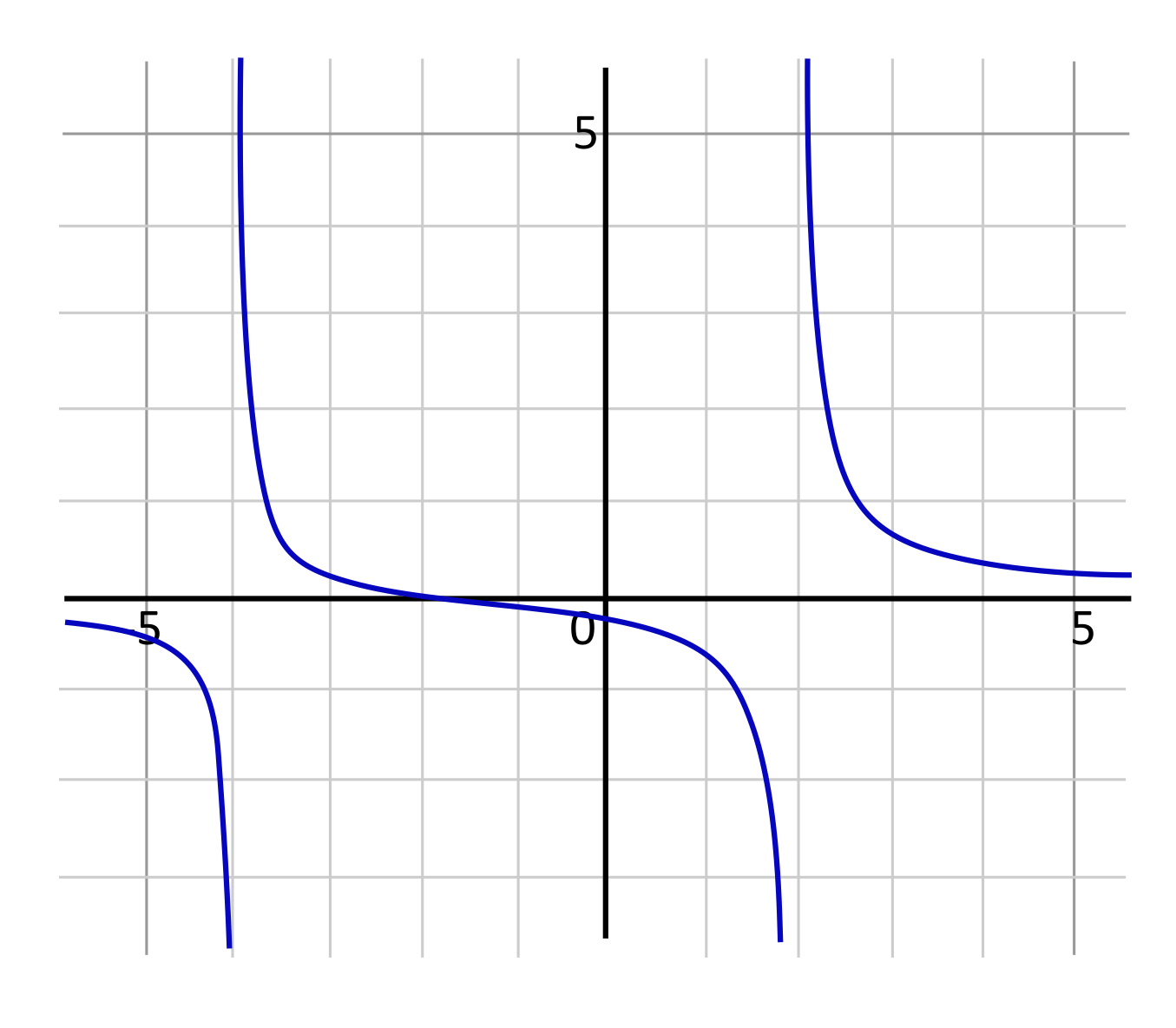
Vertical asymptotes can be identified by looking for the vertical gaps or areas of the graph that the lines avoid. For example, in the graph below, we see two curving lines that are avoiding the line of \(x=-2\). Therefore, the vertical asymptote is \(x=-2\). When a graph is provided, looking for the areas that the lines avoid is a quick way to identify the vertical asymptotes.
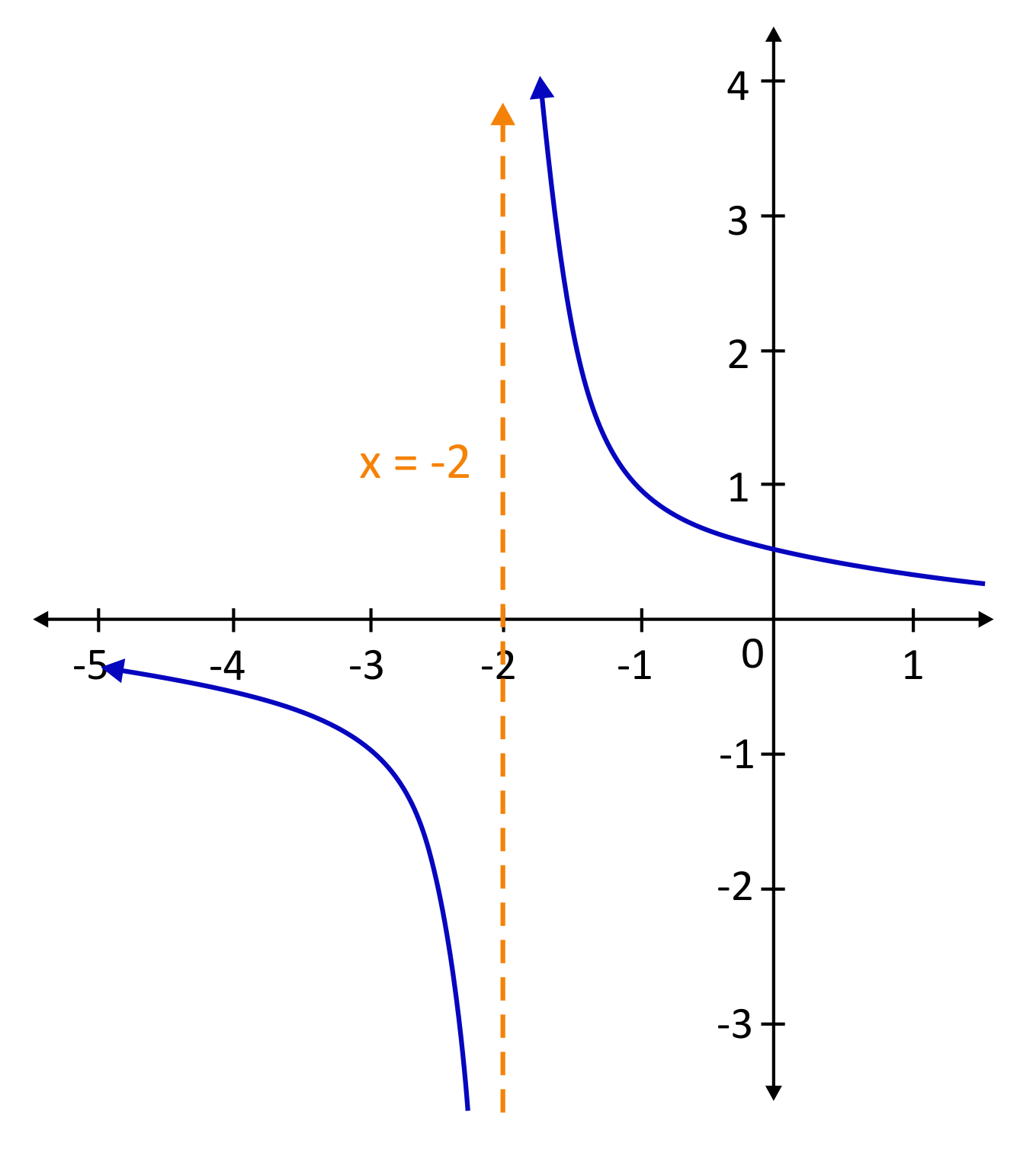
Asymptotes are used frequently in Calculus, and can be connected to many real-world scenarios. For example, years ago when designing an airplane, the vertical asymptote for speed was the speed of sound (this is not the case in today’s modern world). Planes were originally not built to exceed this speed because we did not have the proper materials to withstand the shockwaves. This meant that the asymptote for speed was the speed of sound, because in theory planes would never reach this speed. It can be helpful to think of asymptotes as limits which in theory can never be reached.

Vertical Asymptote Sample Questions
Here are a few sample questions going over vertical asymptotes.
Find the domain and vertical asymptotes of the following function:
\(f(x)=\frac{5}{x-1}\)
The domain of a function is all of the \(x\)-values that produce a non-zero denominator. To find the domain, set the denominator equal to \(0\), and then solve. In this case, \((x-1)=0\) solves to \(x=1\). This means that if \(x\) is \(1\), then the denominator is \(0\). So, the domain is \(x≠1\) because \(x\) can’t be \(1\).
The vertical asymptotes are the regions where the graph can’t go. Since \(x\) can’t be equal to \(1\), the graph can’t be located here. So, we would say that the vertical asymptote is at \(x=1\). The graph can get close to \(x=1\), but never exactly \(x=1\).
Find the domain and vertical asymptotes of the following function:
\(f(x)=\frac{(2x-3)(x+1)(x-2)}{(x+2)(x+1)}\)
To find the domain we set the denominator equal to zero, and then solve. In this case, \((x+2)(x+1)=0\) solves to \(x=-2\) and \(x=-1\). This means that is \(x\) is \(-2\) or \(-1\), the denominator is zero. So, the domain is \(x≠-2,-1\), because \(x\) can’t be these values. Since \(x\) can’t be equal to \(-2\) or \(-1\), the graph can’t be located here. So, the vertical asymptotes are at \(x=-2\) and \(x=-1\). The graph can get close to \(x=-2\) and \(x=-1\), but never exactly \(-2\) or \(-1\).
Find the domain and vertical asymptotes of the following function:
\(f(x)=3x^2-\frac{9}{x^2+7x+12}\)
To identify the domain of the function, set the denominator equal to zero and then solve. Start with \(x^2+7x+12=0\) and then factor this to \((x+3)(x+4)=0\). This shows us that \(x=-3\) and \(x=-4\). This means that if \(x\) is \(-3\) or \(-4\), the denominator will be zero, which can’t happen. The domain can be anything except \(x=-3\) or \(-4\). Since \(x\) can’t be \(-3\) or \(-4\), \(x=-3\) and \(x=-4\) are the vertical asymptotes. The graphed line will curve and bend to avoid these values.
What are the vertical asymptotes for the graph below?
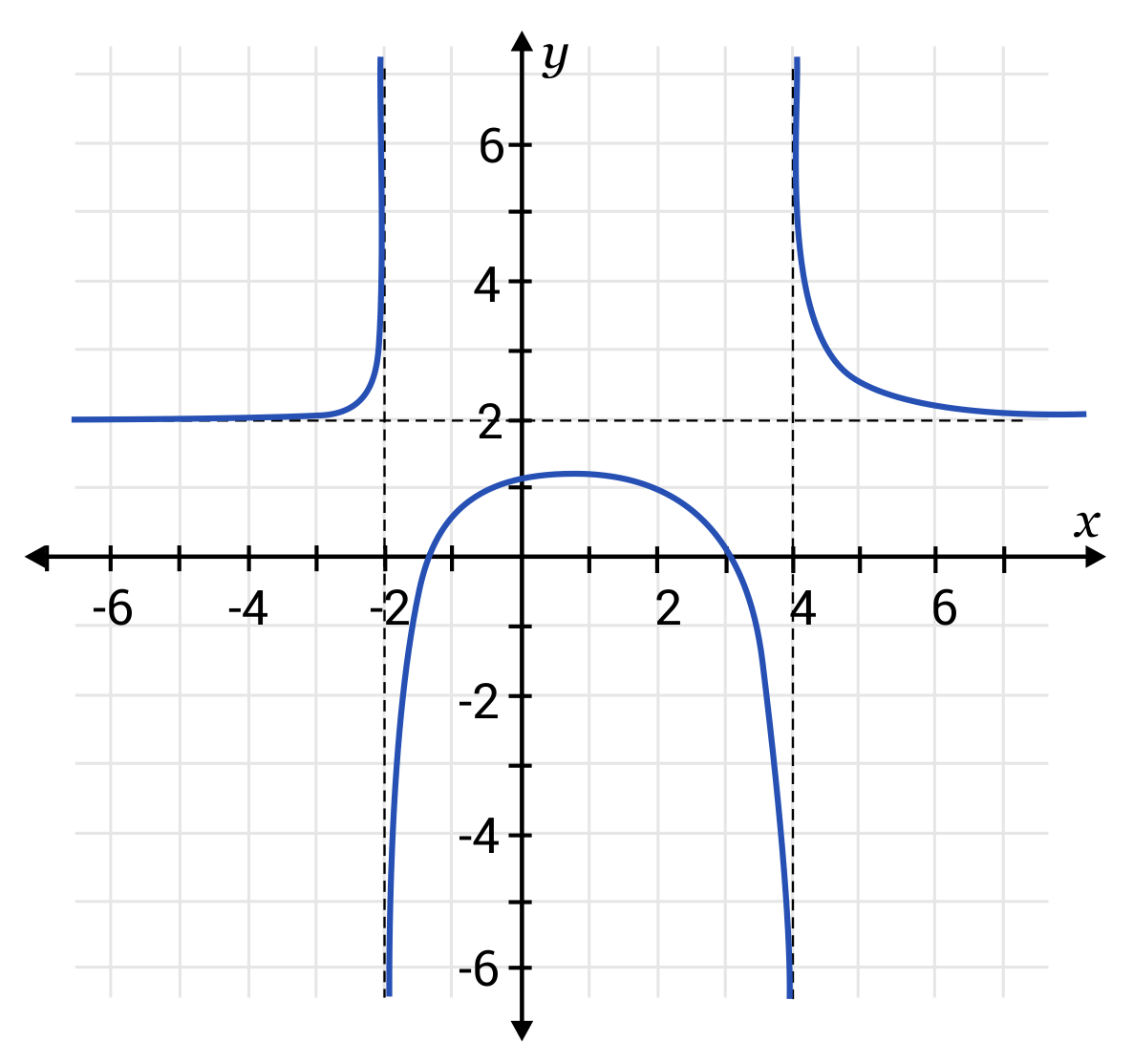
Remember, vertical asymptotes are represented by dotted lines where the graph cannot go. The two \(x\)-values represented by dotted lines are \(x=4\) and \(x=-2\). The graph can bend close to these values, but never land on these values.
What is the vertical asymptote for the following graph?
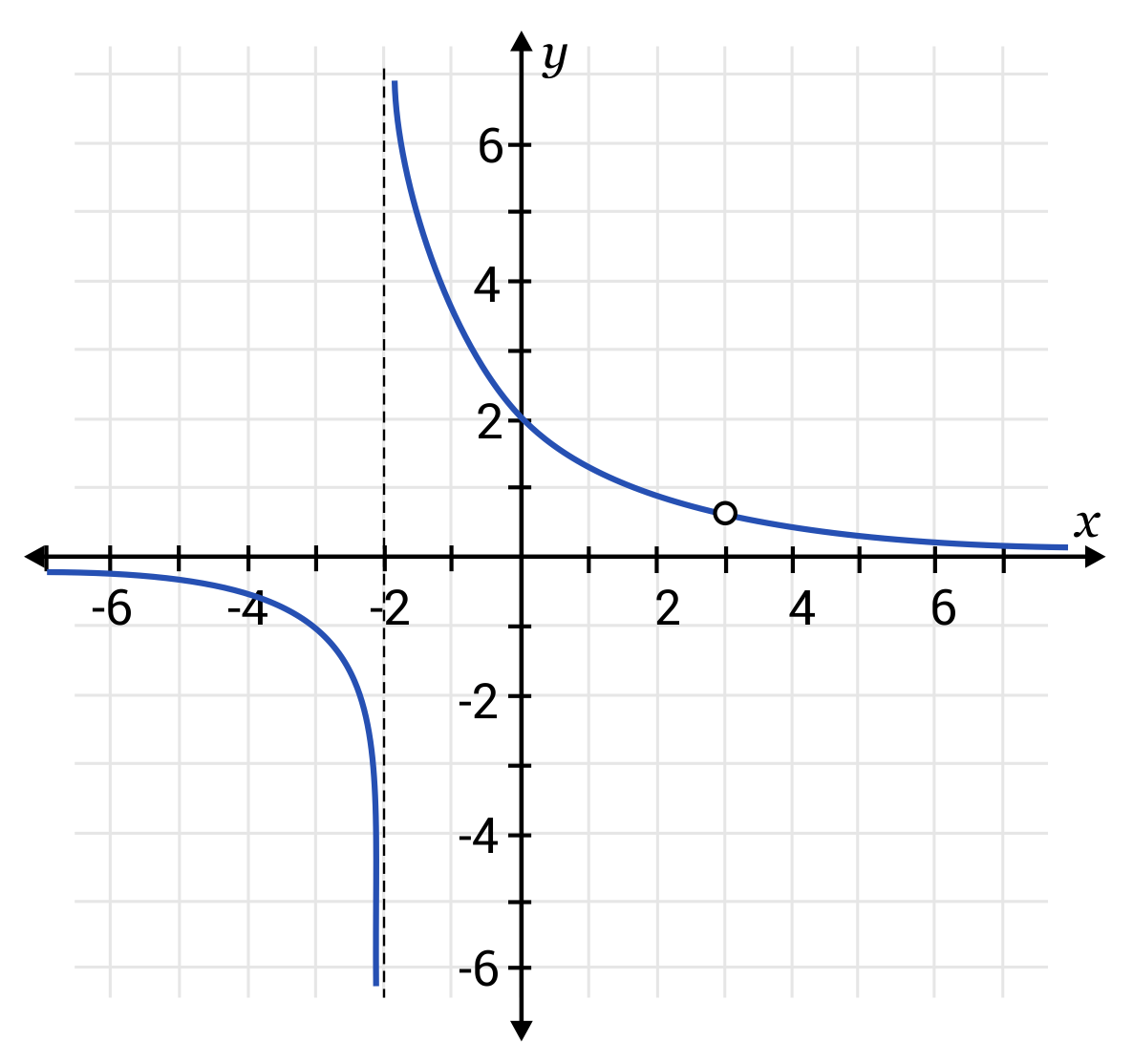
The \(x\)-value represented by dotted line is \(x=-2\). The graph can bend close to this value, but never land on this value.