
An equation is a statement that two mathematical expressions are equal. Expressions represent quantities and can be strictly numerical or contain some combination of numerical terms and terms containing variables. For instance, \(6 + 3\) is a numerical expression, and \(2x – 7\) is an expression that contains a variable.
Equations are like sentences, and they can be evaluated as true or false. For example, \(2 × 5 = 10\) is a true statement because the quantity \(2\times 5\) is equal to the quantity 10. On the other hand, \(25 = 4\times 5\) is a false statement, because the quantity 25 is not equal to the quantity \(4\times 5\).
When equations contain variables, the job of solving is to discover the value(s) of the variables that make the equation true. For example, \(x = 10\) is only true when \(x\) has the value of 10, while \(2x = 10\) is only true when \(x\) has the value of 5.
Typically, equations are approached from the standpoint of “balancing,” “performing inverse operations,” and “isolating the variable.”
Solving Systems of Equations
Here’s an example of how the process of solving equations might be approached.
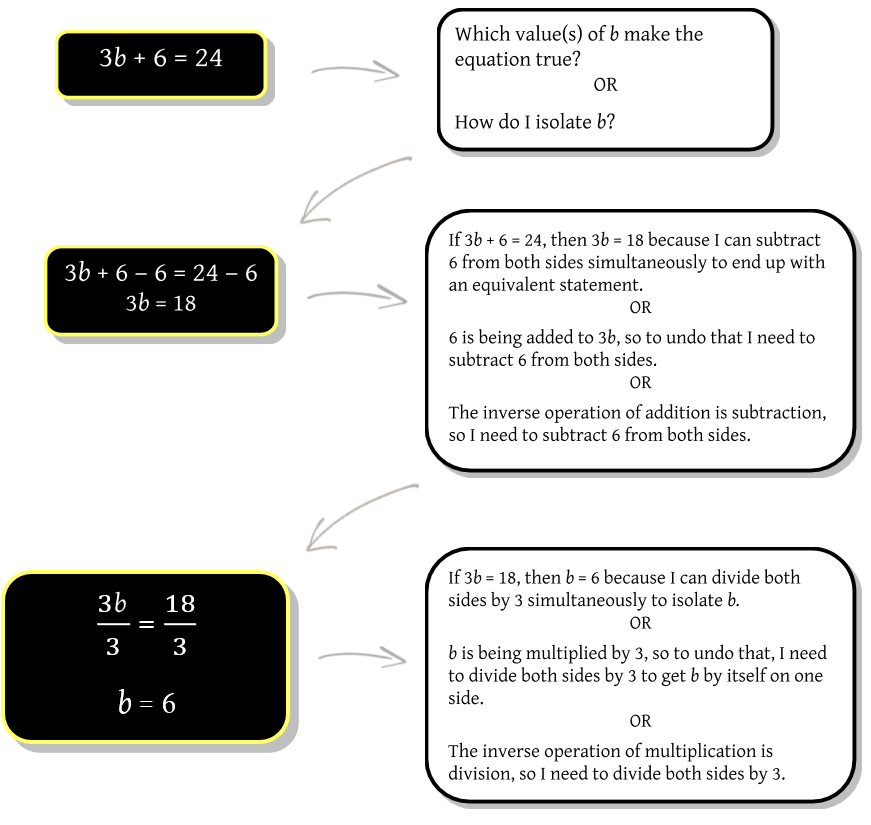
Equations as Scenarios
Expressions often represent quantities that are related in a certain way. Some common examples are\(l\), \(x\), and \(w\), which often represent the area of a rectangle, and \(\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2} \), which often represents the distance between two points on the coordinate plane. Sometimes, we need to create our own equations based on given information.
Example: Max is Ruby’s little brother. Ruby is half of three times Max’s age, and the sum of their ages is 25 years. How old is each sibling?
Let the expression \(a\) represent Max’s age. Then Ruby’s age is represented by the expression \(\frac{3a}{2}\) and the equation we need to solve is \(a+ \frac{3a}{2} = 25\). In other words, Max’s age plus Ruby’s age is 25.
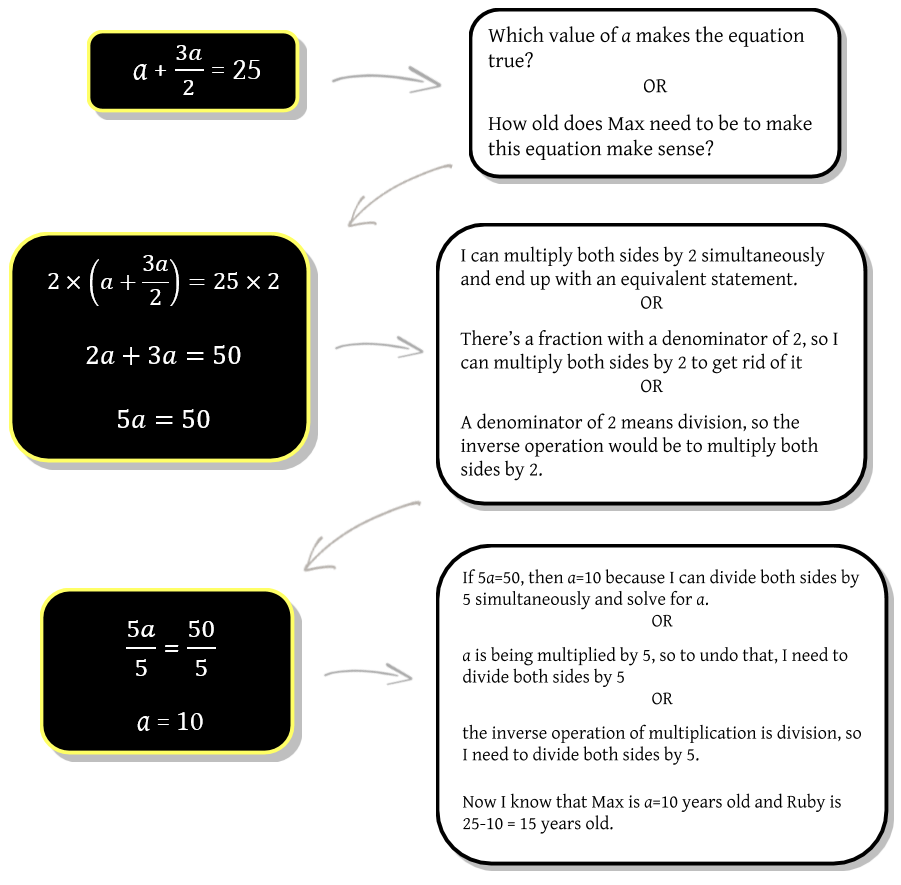
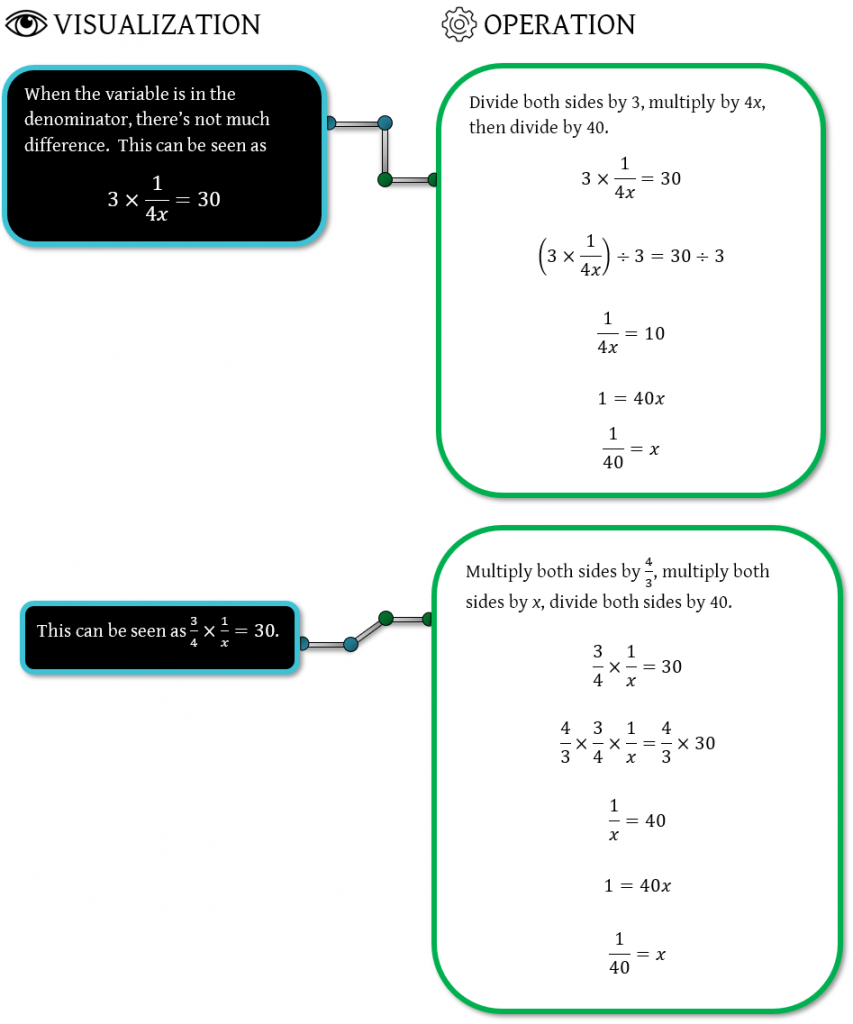
Sometimes, there are multiple ways to visualize an equation. Sometimes, the order we use depends on how we see the terms. For example, let’s look at a couple of different ways we can visualize and solve \(\frac{3x}{4} = 30 \):
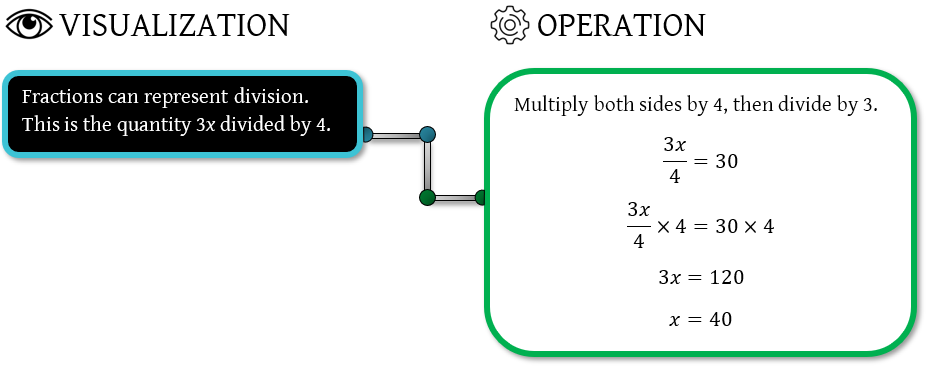
Visualizing the problem this way will lead you down two different paths to solving it:
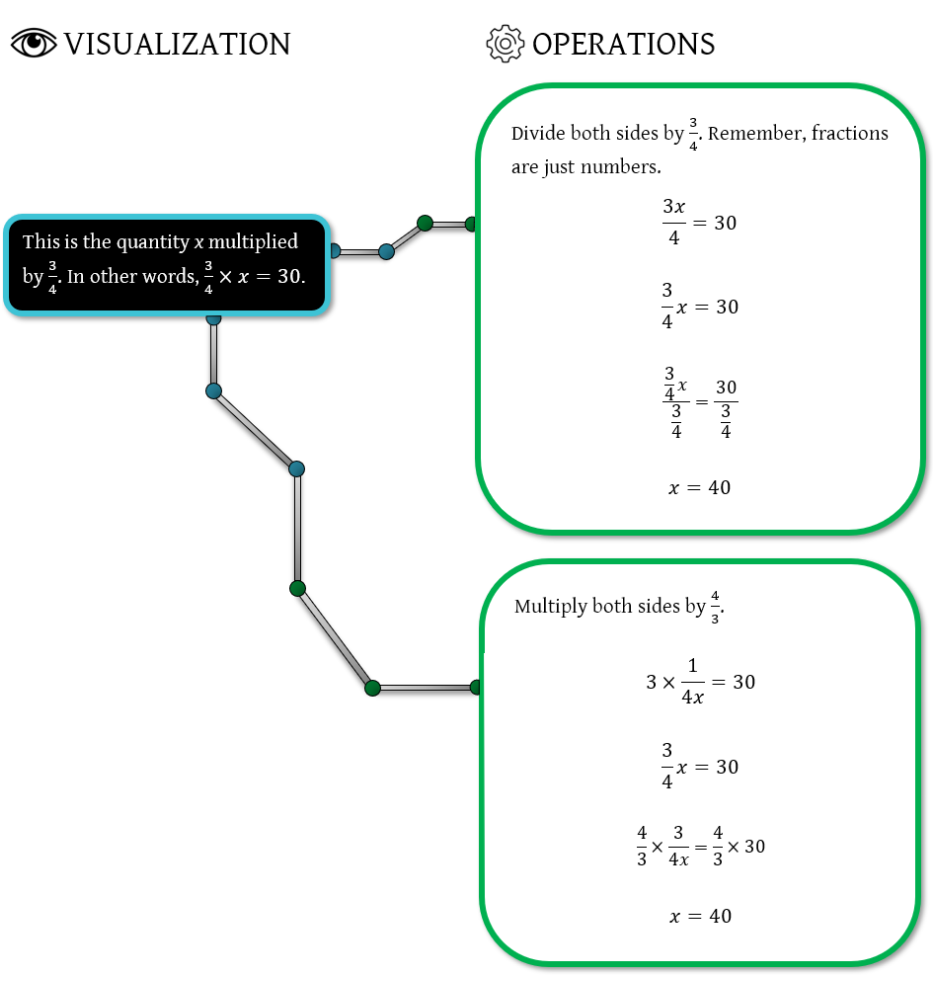
Finally, let’s look at a couple of different ways we can visualize and solve \(\frac{3}{4x} = 30:\)
Hey guys! Welcome to this video over systems of equations.
A system of equations is a group of two or more equations, and each of the equations within the group have at least one unknown variable.
When given a system of equations, the goal is to find the value for each of the unknown variables.
In this video, we will discuss two tools to help you solve for the unknown variables: substitution, and elimination.
Substitution
Substitution is a way of solving the system by getting rid of all of the variables, except for one, then solving for that equation.
The best time to use substitution is when you have a variable that has a coefficient of 1 or -1. The reason why is, because if it has a coefficient of 1 or -1, then you don’t need to undo multiplication or division, you just need to undo addition or subtraction in order to isolate a variable.
There are three steps that you need to follow in order to be able to solve the system using substitution.
- Solve for your \(x\) or \(y\) in one equation.
- Plug your \(x\) or \(y\) in that you solved for into the other equation, then solve.
- Use the number that you get when you solve to solve for the other variable, or variables, depending on how many equations that you have.
So let’s get started!
Example
\(x-9y=-19\)
In this example, we can see that our second equation has a variable with 1 as the coefficient. So, that lets us know to solve for \(x\). Now, you can actually solve for any of the variables. It will just always be easier to solve for one that has a coefficient of 1 or -1.
Now, to do this we just add \(9y\) to both sides.
So, we’ve done what our first step tells us to do and we solved for one of our variables. Step two now tells us to plug in the variable that we have solved for into our other equation, then solve. So we’re going to plug our \(x\) into \(4x+3y = 2\). Because we know that \(x=9y -19\), we’ll plug this into our \(x\)-value here and then solve.
Now that we have it down to one variable, we are able to solve for the value of that variable, so in this case, \(y\).
Let’s rewrite this by multiply our 4 by everything inside our parentheses.
Now we can add our 76 to both sides. You can do this multiple ways. If you wanted to add your \(y\)s together first, then do that. I’m just doing what is easier in my mind.
Once I add my 76 to both sides and add my \(y\)s together, I get \(39y= 78\).
Now, I divide both sides by 39.
Use the number that you get when you solve to solve for the other variable, or variables.
So now all we have to do is take our \(y\)-value and plug it into one of our original equations. It doesn’t matter which one! You can plug it into the first or the second, but I am going to plug it into the second equation, just because.
So that gives you:
\(x – 18 = -19\)
\(x=-1\)
And we’re done! We have found the value of both of our variables using substitution.
Now, let’s take a look at how to solve for a system using elimination.
Elimination
The reason this tool is called elimination is because you add together the two equations in order to eliminate one of your variables.
Example 1
\(7x + 4y = 57\)
We can tell just by looking at it, that our \(y\)s will cancel out. So once we add the two equations together. We have \(10x = 30\).
And we can divide both sides by 10: \(x=3\)
We can take our \(x\)-value and plug it into either of our original equations. I’ll plug it into our first one here. So, we have:
So, and then I’ll rewrite this:
Now, we need to move our 9 to the other side by subtracting 9.
Then we divide both sides by our -4 here.
So now we’ve solved and found both of our variables. That was a good example to learn how elimination works, but it may not always be that our terms cancel so easily.
Like in this example:
Example 2
\(2x + 6y = 34\)
None of our terms cancel right off the bat, so we’ll need to do a little manipulation in order to get them to do what we want them to do.
So, what could we do to get our terms to cancel? Well, there are a couple of things, but the easiest, as it appears to me, is to multiply our first equation by 2. That will allow us to cancel our \(y\)s, because we will be adding a \(-6\) and a \(+6\). So, let’s do that.
We have this equation (\(9x – 3y = -57\)) all being multiplied by 2, so let’s rewrite that and we get:
\(18x – 6y = -114\)
Now, we need to take this and add it to our other equation so we can get our \(y\)s to cancel out. So that would give us \(20x = -80\).
Now, we need to divide both of our sides by 20, which gives us \(x=-4\).
So, now that we know that \(x=-4\), we can plug in our \(-4\) where our \(x\)s are in either one of the original equations.
I’ll plug it into the second one. So we have:
And I’ll simplify this and rewrite it.
Now I’ll move and my 8 to both sides: \(6y=42\).
Now we divide both sides by 6 here: \(y=7\)
So our final answer to this problem is this:
I hope that this video on how to solve a system of equations using substitution and elimination has been helpful.
See you guys next time!
Frequently Asked Questions
Q
How do you solve systems of equations?
A
A system of equations refers to a set or collection of equations that share the same variables. The goal of solving systems of equations is to identify the location where the lines intersect when the equations are graphed. The \((x, y)\) ordered pair of this intersection point is considered the solution of the system. There are generally four methods for solving systems of equations: substitution, elimination, graphing, and matrices. The method that you select depends on the structure of the equations. For example, if the equations are already in slope-intercept form \((y=mx+b)\), then the graphing method is a convenient option.
Q
What are the four methods for solving systems of equations?
A
When solving systems of equations, you have a few options as far as which method you choose. The method that you select will depend on the structure of the equations. Selecting the strategy that is most convenient and efficient is of course the goal. The more you work with systems, the more trained your eye will become in selecting the best method. The four methods to choose from include substitution, elimination, graphing, and matrices. Each approach is quite different, but every strategy will ultimately arrive at the same goal, which is to locate the \((x, y)\) ordered pair where the lines intersect.
Q
Why do we use systems of equations?
A
Systems of equations have many useful real-world applications. For example, whenever you are given two unknown values, as well as information that connects the two unknown values, a system of equations can be set up in order to solve for the two unknowns. For example, let’s say the admission fee to an amusement park is \($20\) for children and \($30\) for adults. Let’s also say that \(215\) people entered the park today, and that the total admission fees collected today was \($3{,}500\). We can solve for the number of children and adult tickets sold by setting up a system of equations. We have two unknown values, and we have enough information connecting the two values to set up our equations. To solve this problem, we first need to select a strategy (substitution, elimination, graphing, or matrices). Solving systems of equations is a skill that has many valuable applications. This is why the process of solving systems is considered a major branch of algebra.
Q
What is the difference between an equation and a system of equations?
A
A linear equation can be graphed by plugging in values for \(x\), and then calculating the corresponding \(y\)-values. These \(x\)– and \(y\)-coordinates can be graphed and will eventually form a line. When there is more than one equation, and they share the same variables, the equations are called a “system”.
An example of a system of equations:
\(y=2x+5\)
\(3y=4x-8\)
Q
What careers use systems of equations?
A
The exciting thing about learning how to solve systems of equations is that the skill can be applied to almost any career! Anytime you are faced with a scenario where you have two unknown values, and enough information to compare the two values, setting up and solving a system of equations will allow you to identify the amount of each value. This is often useful in the field of finance, business, and sales. Specifically careers that involve calculations with costs, revenue, and profit.
Q
How are systems of equations used in real life?
A
Solving systems of equations is a valuable skill to study because of its many applications in the real-world. Anytime we have two unknown values, and enough information to compare the two values, we can solve for the unknowns by setting up a system of equations. Remember, the solution of a system of equations is the value for each variable that makes both of the equations true. This skill has applications in many areas of our daily lives. For example, we can use a system of equations to determine how many calories we burn using different machines at the gym. If we use the rowing machine for \(30\) minutes and the treadmill for \(20\) minutes, and we burn a total of \(430\) calories, this can be set up as equation #1: \(30r+20w=430\). If we go to the gym the following day and use the rowing machine for \(50\) minutes and the treadmill for \(10\) minutes, burning a total of \(600\) calories, this can be set up as equation #2: \(50r+10w=600\). We have two unknown values (how many calories we burn per minute on each machine), and we have enough information comparing both of the values. This means that we can solve the problem by setting up and solving a system of equations.
Q
How do you solve systems of equations by substitution?
A
Solving systems of equations by substitution follows three basic steps.
Step 1: Solve one equation for one of the variables.
Step 2: Substitute this expression into the other equation, and solve for the missing variable.
Step 3: Substitute this answer into one of the equations in order to solve for the other variable.
Q
What is the substitution method with an example?
A
The following system of equations can be solved in three steps.
\(2x+y=1\)
\(x-2y=8\)
Step 1: Solve one equation for one of the variables.
Look for the equation with a coefficient of \(1\) or \(-1\). This makes the solving process quicker. \(x-2y=8\) has a coefficient of \(1\) for \(x\), so let’s solve for \(x\). When \(2y\) is added to both sides of the equation \(x-2y=8\) becomes \(x=8+2y\).
Step 2: Substitute this expression into the other equation, and solve for the missing variable.
\(x=8+2y\) has been solved for \(x\), so plug this expression into the other equation for \(x\). \(2x+y=1\) becomes \(2(8+2y)+y=1\).
Now we have an equation with only the y-variable. At this point we can solve for y. First we distribute, so \(2(8+2y)+y=1\) becomes \(16+4y+y=1\). Now we combine like-terms. \(16+4y+y=1\)becomes \(16+5y=1\). Now subtract \(16\) from both sides, divide by \(5\), and we see that \(y=-3\).
Step 3: Substitute this answer into one of the original equations in order to solve for the other variable.
Now that we know\(y=-3\), we can solve for \(x\). Plug \(-3\) in for \(y\), in either equation. Let’s use the first equation \(2x+y=1\). When \(-3\) is plugged in for \(y\), the equation becomes \(2x+(-3)=1\). When we solve for \(x\), we see that \(x=2\).
We know that \(x=2\) and \(y=-3\). This means that the ordered pair \((2, -3)\) is the solution of the system of equations. This location is where the lines will cross each other when graphed.
Q
How do you do elimination in algebra?
A
Systems of equations can be solved using elimination. This method follows three basic steps. Step 1: Manipulate the equations so that one variable will cancel out when the equations are added or subtracted. Step 2: Add or subtract the equations so that one variable is eliminated. Solve for the remaining variable. Step 3: Plug the solved variable back into one of the original equations in order to solve for the other variable.
For example, the following system can be solved by elimination.
\(3x-4y=-5\)
\(5x+8y=-1\)
Step 1: Manipulate the equations so that one variable will cancel out when the equations are added or subtracted.
In this case, we can multiply the first equation by \(2\), so that the \(y\)-variables will cancel out when the equations are added. \(3x-4y=-5\) becomes \(6x-8y=-10\).
Step 2: Add or subtract the equations so that one variable is eliminated. Solve for the remaining variable.
\(6x-8y=-10\)
\(5x+8y=-1\)
When the equations are added, the result is \(11x=-11\). Now we can solve for \(x\) by dividing both sides of the equation by \(11\). \(x=-1\).
Step 3: Plug the solved variable back into one of the original equations in order to solve for the other variable.Let’s plug \(-1\) in for \(x\) in the first equation \(3x-4y=-5\). The equation now becomes \(3(-1)-4y=-5\) which simplifies to\(y=\frac{1}{2}\).
\(x=-1\) and \(y=\frac{1}{2}\) which means that the solution to the system of equations is the ordered pair \((-1, \frac{1}{2})\). If the two original equations were graphed, this ordered pair is where the two lines would intersect.
Q
How do you solve a \(3×3\) system by elimination?
A
Sometimes a system will have more than two equations. For example the following system has three equations.
\(x+2y-z=2\)
\(2x-3y+z=-1\)
\(5x-y-2z=-3\)
The process for solving a system of three equations will be the same as the process for two equations. However, our first objective is to go from three equations down to two. This can be achieved by adding or subtracting two of the equations. Let’s add the first two equations.
| \(\phantom{00}x+2y-z=2\) | ||
| \(+\) | \(2x-3y+z=-1\) | |
| \(3x-y=1\) |
The variable \(z\) has dropped out, and now we only have two equations which means we are on the right track. However, we need to incorporate the third equation into the mix. Let’s do this by multiplying the second equation by \(2\), and then adding this to the third equation.
The second equation becomes \(4x-6y+2z=-2\) and when we add this to the third equation, we get \(9x-7y=-5\) (The \(z\)s dropped out!).
At this point, we are simply solving a two equation system with two variables.
\(3x-y=1\) (Multiply this equation by \(-7\) so that the \(y\)-variables will be eliminated when the equations are added together)
| \(-21x+7y=-7\) | ||
| \(+\) | \(\phantom{0}9x-7y=-5\) | |
| \(-12x=-12\) |
Now plug in \(1\) for \(x\) in any of the equations.
\(3(1)-y=1\)
\(y=2\)
Finally, plug in \(x=1\) and \(y=2\) to any of the equations and solve for \(z\). If these values are plugged into the first equation, \(x+2y-z=2\) becomes \((1)+2(2)-z=2\), which simplifies to \(z=3\).
Remember, when you have a system with three equations and three variables, the big idea is to work your way down to two equations with two variables, and eventually one equation with one variable. The more you practice these elimination problems the easier they will become!
Q
Can you subtract systems of equations?
A
When solving a system of equations using the elimination method, the equations can be added or subtracted in order to eliminate a variable. For example, if you notice that both equations have the same variable with the same sign, then elimination using subtraction is likely the most efficient method.
For example, see if you can identify why subtraction with elimination is the best option for solving the following system.
\(-5x-3y=30\)
You’re correct if you noticed that both equations have the same variable with the same sign: \(-3y\) and \(-3y\). This means that if one of the equations is subtracted from the other, the term will drop out, leaving only one variable (that’s the goal).
| \(\phantom{000}2x-3y=9\) | ||
| \(–\) | \((-5x-3y=30)\) | |
| \(7x=-21\) |
Now \(-3\) can be plugged into one of the original equations in order to solve for \(y\).
\(2x-3y=9\) becomes \(2(-3)-3y=9\) which simplifies to \(y=-5\). \((-3, -5)\) is the solution.
System of Equations Practice Problems
Use the substitution method to solve the following system of equations:
\(y=3x+2\)
\(y=5x+6\)
Step 1. To use the substitution method, solve one equation for one of the variables and substitute it into the other equation to find the value of the other variable. Both equations are already solved for \(y\), so we will substitute \(y=3x+2\) into the second equation to get:
\(3x+2=5x+6\)
Step 2. Now, solve the new equation for \(x\).
Step 3. Next, substitute the value for \(x\) into either of the two original equations to find the \(y\)-value. Substituting into the first equation results in:
\(y=3-2+2\)
\(y=-6+2\)
\(y=-4\)
Step 4. Write the answer as the ordered pair \((-2,-4)\).
Use the elimination method to solve the following system of equations:
\(2x-3y=-9\)
\(x+4y=23\)
Step 1. Manipulate the equations so that one variable will cancel out when the equations are added or subtracted. We can multiply the second equation by \(–2\) so that the \(x\)-variables are eliminated when the two equations are combined.
\(-2x+4y=23\)
\(-2x-8y=-46\)
Step 2. Combine the two equations to eliminate \(x\). Then solve the resulting equation for \(y\).
| \(\phantom{-}2x-3y=-9\) \(-2x-8y=-46\) | Line the two equations up that will be combined. |
| \(-11y=-55\) | Combine the two equations to eliminate the \(x\)-variable. |
| \(\frac{-11y}{11}=\frac{-55}{-11}\) | Divide both sides of the equation by \(–11\). | \(y=5\) | Simplify to find \(y\). |
Step 3. Now we can substitute the \(y\)-value into either of the original equations to find the \(x\)-value. Substituting \(y=5\) into the second equation, we get:
\(x+4(5)=23\)
\(x+20=23\)
\(x+20-20=23-20\)
\(x=3\)
Step 4. Write the answer as the ordered pair \((3,5)\).
Use the elimination method to solve the following system of equations:
\(x+\frac{1}{3}y=7\)
\(3x-y=9\)
Step 1. Manipulate the equations so that one variable will cancel out when the equations are added or subtracted. We can multiply the first equation by \(3\) so that the \(y\)-variables are eliminated when the two equations are combined.
\(3(x+\frac{1}{3}y=7)\)
\(3x+y=21\)
Step 2. Combine the two equations to eliminate \(y\). Then solve the resulting equation for \(x\).
| \(3x+y=21\) \(3x-y=9\) | Line the two equations up that will be combined. |
| \(6x\phantom{+y}=30\) | Add the two equations to eliminate the \(y\)-variable. |
| \(\frac{6x}{6}=\frac{30}{6}\) | Divide both sides of the equation by \(6\). | \(x=5\) | Simplify to find \(x\). |
Step 3. Now we can substitute the \(x\)-value into either of the original equations to find the \(y\)-value. Substituting \(x=5\) into the first equation, we get:
\(5+\frac{1}{3}y=7\)
\(5+\frac{1}{3}y-5=7-5\)
\(\frac{1}{3}y=2\)
\(3(\frac{1}{3}y)=3∙2\)
\(y=6\)
Step 4. Write the answer as the ordered pair \((5,6)\).
The sum of two numbers is 75. Four times the smaller number equals the larger number. What are the two numbers?
Step 1: Let \(x\) be the smaller number and \(y\) be the larger number. The sum of the two numbers is 75, so:
\(x+y=75\)
Since the larger number is four times the smaller number, we also have:
\(y=4x\)
We can solve the following system of linear equations to find each number:
\(x+y=75\)
\(y=4x\)
Step 2. Since the second equation is solved for \(y\), we will use the substitution method by substituting its value into the first equation.
\(x+4x=75\)
Step 3. Now, solve the first equation for \(x\).
| \(\phantom{-}x+(4x)=75\) \(-2x-8y=-46\) | Write the first equation with the substituted value. |
| \(5x=75\) | Combine like terms on the left-hand side of the equation. |
| \(\frac{5x}{5}=\frac{75}{5}\) | Divide both sides by 5. | \(x=15\) | Simplify each side of the equation. |
Step 4. Next, substitute the value for \(x\) into either of the two original equations to find the \(y\)-value. Substituting our value for \(x\) into the first equation, we have:
Step 5. Since \(x=15\) and \(y=60\), the two numbers are \(15\) and \(60\).
A local fast-food restaurant sells hotdogs for $2.75 each and hamburgers for $4.50 each. During a given lunch rush, the restaurant sells a combined total of 225 hotdogs and hamburgers for a combined revenue of $881.25. How many hotdogs and how many hamburgers did the restaurant sell during the lunch rush?
Step 1. Let \(x\) be the number of hot dogs sold and \(y\) be the number of hamburgers sold, then:
\(x+y=225\)
The revenue generated by the hot dog sales is \(2.75x\), and the revenue generated by the hamburger sales is \(4.50y\). Since the combine revenue equals $881.25, we have:
\(2.75x+4.50y=881.25\)
So, we have the following system of equations:
\(x+y=225\)
\(2.75x+4.50y=881.25\)
We will use the elimination method by manipulating the equations so that one variable will cancel out when the equations are added or subtracted. We can multiply the first equation by –2.75 so that the \(x\)-variables are eliminated when the two equations are combined.
\(-2.75x+y=225\)
\(-2.75x-2.75y=-618.75\)
Step 2. Now combine the two equations to eliminate \(x\). Then solve the resulting equation for \(y\).
Step 3. Now we can substitute the \(y\)-value into either of the original equations to find the \(x\)-value. Substituting \(y=150\) into the first equation, we get:
\(x+150=225\)
\(x+150-150=225-150\)
\(x=75\)
So, the restaurant sold 75 hot dogs and 150 hamburgers.

