Squeeze Theorem
Hello and welcome to this video about the squeeze theorem! When calculating limits, occasionally we run into examples that cannot be evaluated by the more “conventional” methods – direct substitution is inconclusive, algebra proves fruitless, even graphing may not give a clear picture. Sometimes, we can actually squeeze a function between two other functions to determine a limit. For this reason, the theorem is also referred to as:
- the sandwich theorem
- the sandwich rule
- the police theorem
- the pinching theorem
- the squeeze lemma
- and, in Italy, the theorem of carabinieri
Let’s see it in action with a familiar limit we know before stating it formally. We know:
\(\lim_{x \rightarrow 0}\frac{sinx}{x}=1\)Substituting 0 yields the indeterminate form 00, but we can’t use algebra to find the limit because the numerator and denominator can’t be simplified. We can see the limit on a graph:
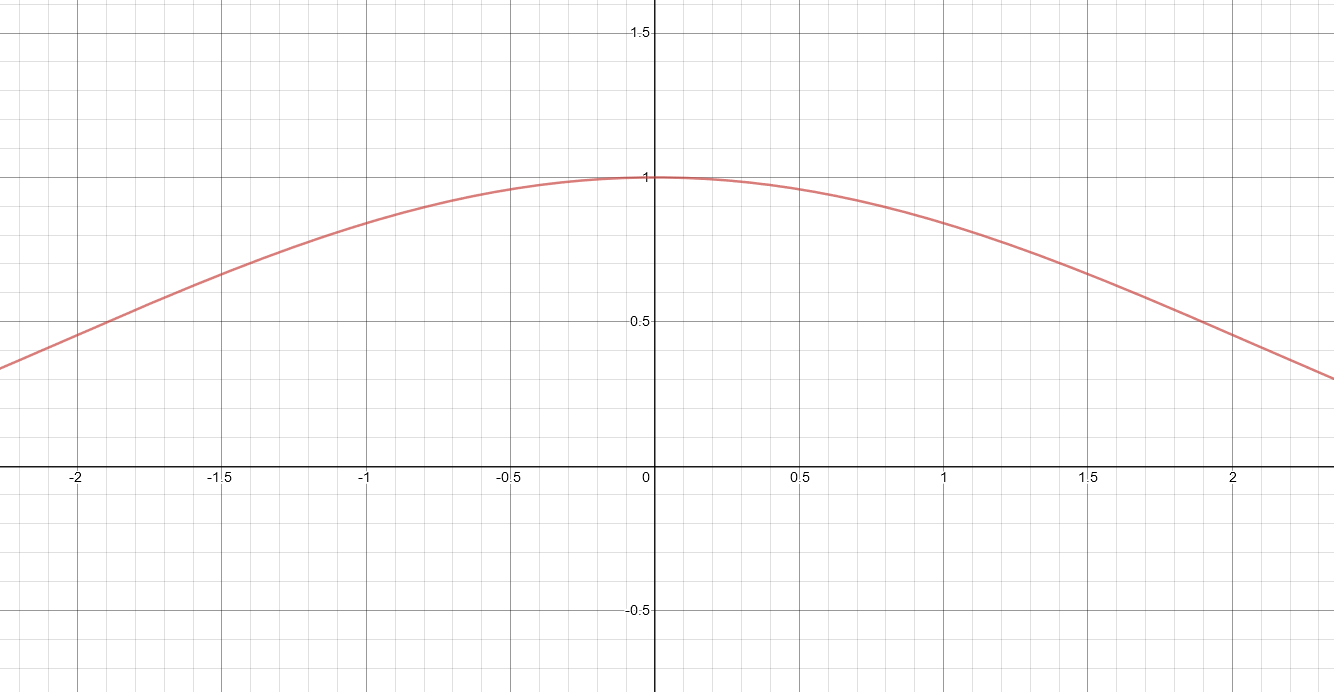
We can use L’Hôpital’s Rule:
Another option is to use the squeeze theorem. This graph shows that \(\frac{sin x}{x}\) is between the cosine function and the horizontal line y=1.
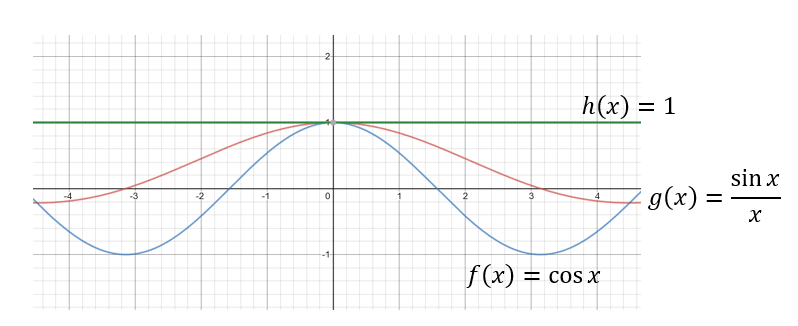
When looking for the “between-ness”, we’ll zoom in close to x = 0.
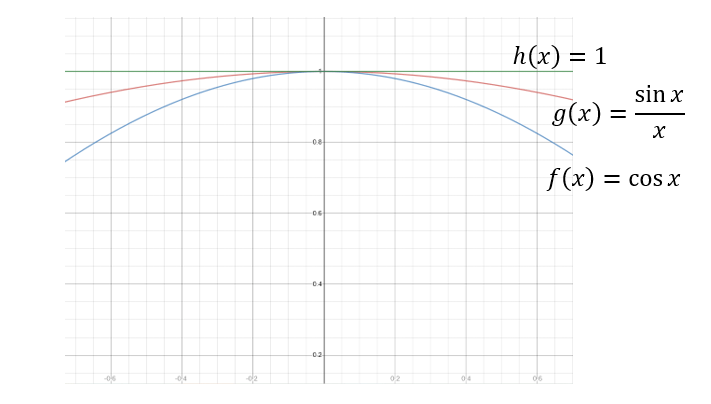
No matter how close we zoom in to the graph, \(\frac{sin x}{x}\) will always be between cos x and 1. By between, we are referring to the function outputs. Let’s zoom in numerically. Of course we can’t use 0, but we can use numbers really close to 0:
| x | -0.1 | -0.01 | 0.01 | 0.1 |
| h(x)=1 | 1 | 1 | 1 | 1 |
| \(g(x)=\frac{sin x}{x}\) | 0.998 | 0.99998 | 0.99998 | 0.998 |
| f(x)=cos x | 0.995 | 0.99995 | 0.99995 | 0.995 |
No matter how close to 0 we get, the values of g(x) are always between the values of f(x) and h(x).
So what does this do for us? Well, since we know these two things, we automatically know \(\lim_{x \rightarrow 0}\frac{sin x}{x}=1\)
- \(\frac{sin x}{x}\) is between cos x and 1 around x = 0,
- \(\lim_{x \rightarrow 0}cos x=\lim_{x \rightarrow 0}1=1\)
\(\frac{sin x}{x}\) is squeezed between cos x and 1 around x=0. Since cos x and 1 both approach 1 as x approaches 0, then \(\frac{sin x}{x}\) must as well. It’s sort of an indirect way of finding a limit and it’s easy to see why names like squeeze, pinch, sandwich and police are used to describe the theorem.
Now for the formal statement:
If \(f(x)≤g(x)≤h(x)\) and \(\lim_{x \rightarrow a}f(x)=\lim_{x \rightarrow a}h(x)=L\), then \(\lim_{x \rightarrow a}g(x)=L\).
Using the theorem often involves more of a proof-like approach than a method and there are often many ways to use it to prove the value of a limit. For example, with the previous limit, we didn’t need to use the functions cos x and 1 as upper and lower bounds. We could have used \(x^2+1\) and \(-x^2+1\) since they both approach 1 as x approaches 0 and \(\frac{sin x}{x}\) is between them:
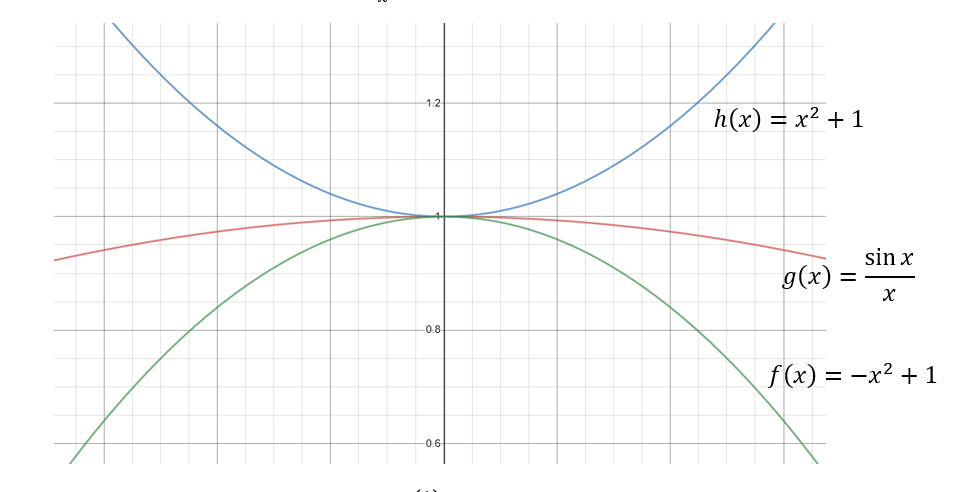
Let’s use the squeeze theorem to find \(\lim_{x \rightarrow 0}x^2cos(\frac{1}{x})\). The table and graph show the function oscillates around the x-axis, but the limit is 0:
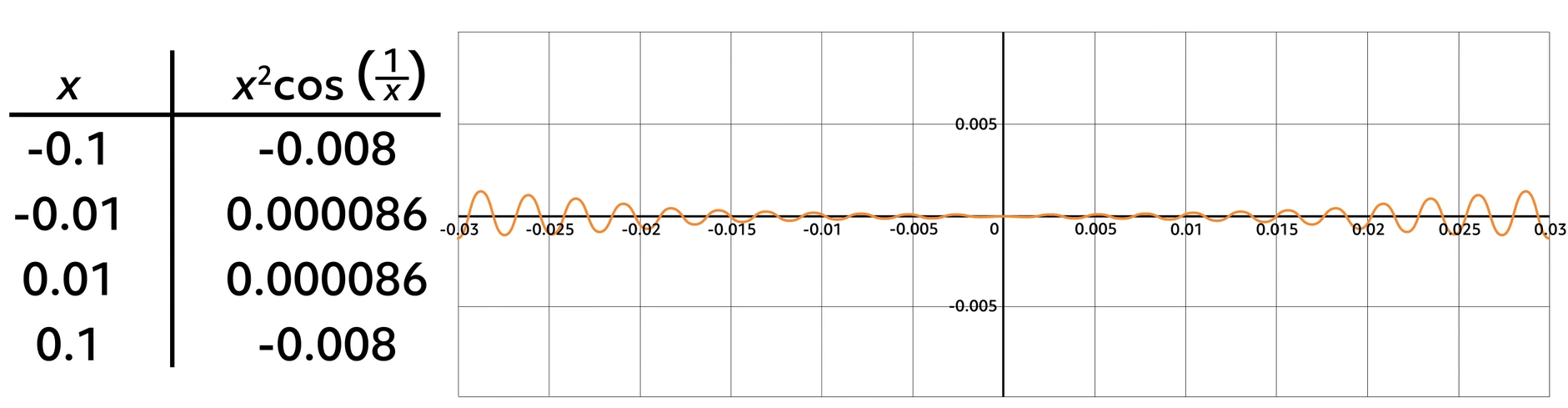
Using substitution and algebra is fruitless, so we’ll begin with the \(cos (\frac{1}{x}\) piece, because that x in the denominator is what’s really complicating things.
Based on our knowledge of the cosine function, we know:
\(-1≤cos (\frac{1}{x}) ≤1\)Now multiply all three parts of the sentence by \(x^2\), because the result will be the original function:
\(-x^2≤x^2 cos \frac{1}{x}≤ x^2\)This tells us how to squeeze the function: put it between \(-x^2\) and \(x^2\). Let’s take a look.
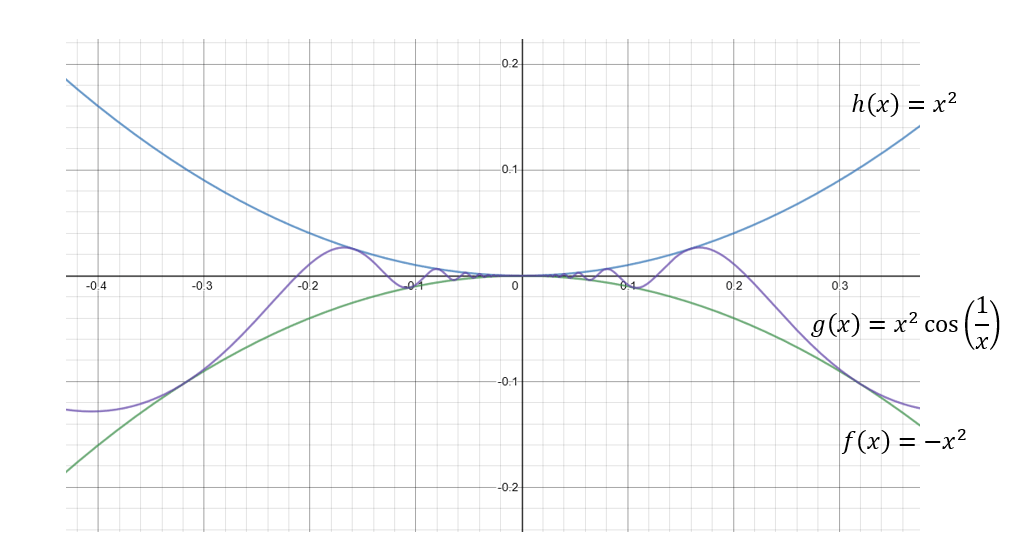
According to the theorem, since \(\lim_{x \rightarrow 0}x^2=\lim_{x \rightarrow 0} -x^2 =0\) and \(x^2cos (\frac{1}{x}\) is between \(x^2\) and \(-x^2\), \(\lim_{x \rightarrow 0}x^2cos (\frac{1}{x})=0\).
Suppose \(f(t)=-\frac{2}{3}t^3+t^2+\frac{1}{3}\) and \(h(t)=cos \frac{tπ}{2}\). If f(t)≤g(t)≤h(t), use the squeeze theorem to show that \(\lim_{t \rightarrow 2}g(t)=-1\)
Now, we don’t know what g(t) is, but with the squeeze theorem we can prove this limit. All we need to show is the limits of f(t) and h(t) are the same as x approaches 2. Since we know that g(t) is pinched in between them, if those limits match, we’ll have our limit.
\(\lim_{t \rightarrow 2}f(t)=-\frac{16}{3}+4-\frac{1}{3}=-1\) and \(\lim_{t \rightarrow 2}h(t)=cos(π)=-1\).
Since the limits of f(t) and h(t) are both -1 and they are squeezing g(t),\(\lim_{t \rightarrow 2}g(1)=-1\).
Let’s try one more!
If \(-\frac{x^2}{4}-\frac{x}{2}≤f(x)≤\sqrt{-\frac{1}{9x}}\), use the squeeze theorem to find \(\lim_{x \rightarrow -1}f(x)\) .
\(\lim_{x \rightarrow -1}-\frac{x^2}{4}-\frac{x}{2}=-\frac{1}{4}+\frac{1}{2}=\frac{1}{4}\)
\(\lim_{t \rightarrow -1}\sqrt{-\frac{1}{9x}}=\sqrt{\frac{1}{9}}=\frac{1}{3}\)
In this case, f(x) is between the two functions, but it’s not being squeezed. Since their limits as x approaches -1 do not match, the best we can say is that \(\lim_{t \rightarrow -1}f(x)\) is between \(\frac{1}{4}\) and \(\frac{1}{3}\).
Thanks for squeezing a little time out of your busy schedule to explore this theorem! I hope this video helped you understand when it’s needed and how it works!
See you next time!
Squeeze Theorem Practice Questions
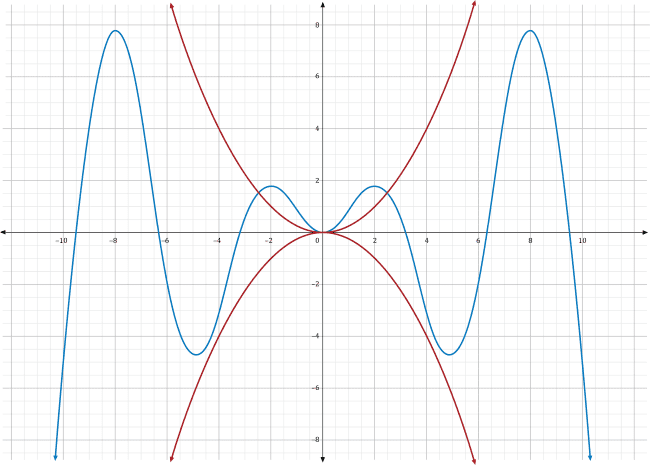
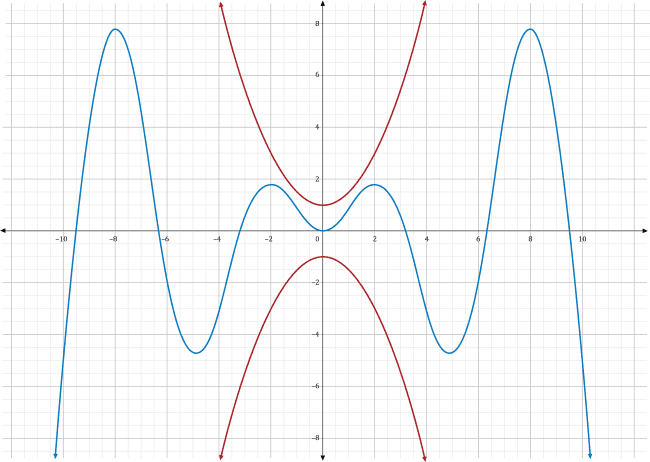
Which of the following sets of functions \(f\left(x\right)\) and \(h\left(x\right)\) (denoted with red lines) would be most appropriate to use to apply the squeeze theorem and find the \(g(x)\) (where \(g\left(x\right)\) is shown as a blue line)?
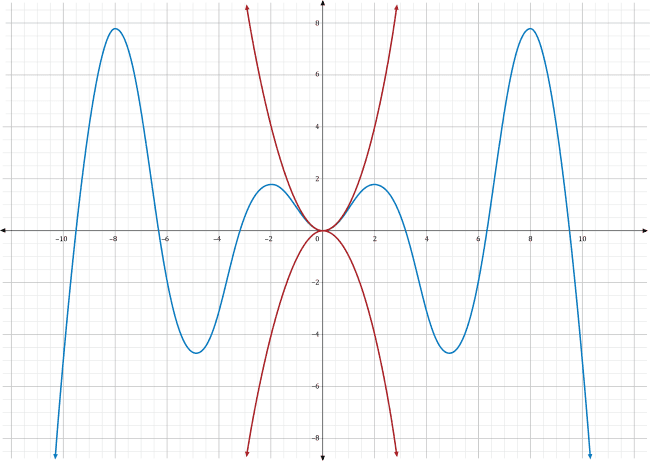
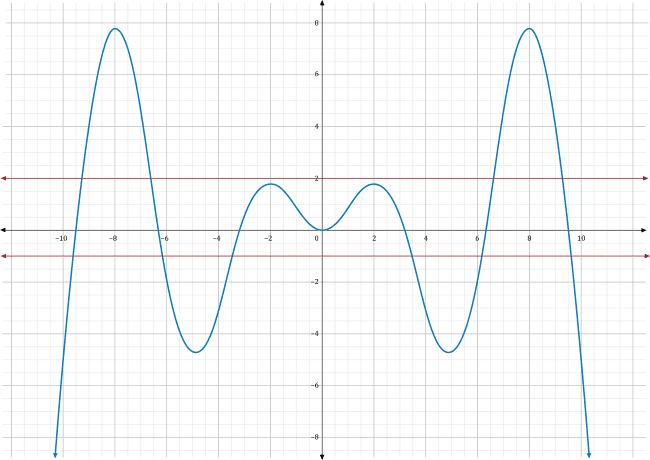
The squeeze theorem states that if \(f\left(x\right)\), \(g\left(x\right)\), and \(h\left(x\right)\) are functions such that \(f\left(x\right)\le g\left(x\right)\le h\left(x\right)\) and \(lim_{x\rightarrow a}\ f\left(x\right)=lim_{x\rightarrow a}\ h\left(x\right)=L\), then the limit \(lim_{x\rightarrow a}g\left(x\right)=L\). In other words, one way to find the limit of a function \(g\left(x\right)\) as \(x\) approaches some point \(a\) is by finding two functions \(f\left(x\right)\) and \(h\left(x\right)\) that enclose \(g\left(x\right)\). If \(f\left(x\right)\) and \(h\left(x\right)\) come to the same limit \(L\) as \(x\) approaches \(a\), then the \(g(x)\) must equal \(L\) too. Notice the two conditions of the squeeze theorem: the functions \(f\left(x\right)\) and \(h\left(x\right)\) need to be above and below \(g\left(x\right)\), respectively, and they both need to come to the same limit value.
In choice A, the two red functions both fall below \(g\left(x\right)\) in the area near \(x=0\). Since the limit is taken in that region, these two red functions are not usable for the squeeze theorem.
Choice B depicts two red functions which are fully above and fully below \(g\left(x\right)\), including the area near \(x=0\). However, they approach two different \(y\)-values as \(x\) approaches zero. The top function approaches \(y=1\) while the bottom function approaches \(y=-1\). These two functions will not allow you to find the exact value of the limit of \(g\left(x\right)\) as \(x\) approaches zero.
Choice C shows two red functions which are entirely above and entirely below \(g\left(x\right)\), respectively. Additionally, as \(x\) approaches zero, they both approach the same value, \(y=0\). For these reasons, the two red functions in choice C are usable for the squeeze theorem. Further, they suggest that the limit \(g\left(x\right)=0\).
Choice D shows two red functions which are above and below \(g\left(x\right)\) near \(x=0\). However, they are approaching different values. The top function is going to 2 while the bottom is going to –1. These two functions will not allow you to find the exact value of the limit of \(g\left(x\right)\) as \(x\) approaches zero.
Given that \(f\left(x\right)=-2x^2+12x-18\), \(h\left(x\right)=\frac{1}{3}x^2-2x+3\), and \(f\left(x\right)\le g\left(x\right)\le h\left(x\right)\), use the squeeze theorem to determine \(\lim_{x \to 3}g(x)\) .
Even though the problem doesn’t explicitly state the function \(g\left(x\right)\), the squeeze theorem can help determine the limit of \(g\) as \(x\) approaches 3, as long as the two conditions of the theorem are met.
The squeeze theorem says that if \(f\left(x\right)\le g\left(x\right)\le h\left(x\right)\) and \(f(x)=h(x)=L\), then the limit \(g(x)\) is also L. In this problem, the first condition, \(f\left(x\right)\le g\left(x\right)\le h\left(x\right)\), is given as true. This means to find the limit of \(g\left(x\right)\) as \(x\) approaches 3, check if \(f\left(x\right)\) and \(h\left(x\right)\) both come to the same limit at that point, and determine the value of those limits.
For this problem, the limits of \(f\left(x\right)\) and \(h\left(x\right)\) as \(x\) approaches 3 can be determined by plugging in \(x=3\).
\(f\left(x\right)=\left(-2x^2+12x-18\right)\)
\(=-2\left(3\right)^2+12\left(3\right)-18\)
\(=-2\left(9\right)+12\left(3\right)-18\)
\(=-18+36–18\)
\(=0\)
\(h(x)=\left(\frac{1}{3}x^2-2x+3\right)\)
\(=\frac{1}{3}\left(3\right)^2-2\left(3\right)+3\)
\(=\frac{1}{3}\left(9\right)-2\left(3\right)+3\)
\(=3-6+3\)
\(=0\)
So \(f(x)=h(x)=0\). Since both limits have the same value, zero, the squeeze theorem dictates that the limit of \(g\left(x\right)\) as \(x\) approaches 3 must also be zero.
\(g(x)=0\)
Let \(a\left(x\right)=\frac{1}{4}x^2+x+3\) and \(c\left(x\right)=x^2+4x+6\). Apply the squeeze theorem to determine the value of \(\lim_{x \to -2}b(x)\) given that \(a\left(x\right)\le b\left(x\right)\le c\left(x\right)\).
It is stated that \(b\left(x\right)\) lies between \(a\left(x\right)\) and \(c\left(x\right)\), so all that is needed to apply the squeeze theorem is determining whether \(a\) and \(c\) have the same limit as \(x\) approaches –2. Both of those limits can be found by plugging in \(x=-2\).
\(a(x)=\frac{1}{4}\left(-2\right)^2+\left(-2\right)+3\)
\(=\frac{1}{4}\left(4\right)-2+3\)
\(=1-2+3\)
\(=2\)
\(c(x)=\left(-2\right)^2+4\left(-2\right)+6\)
\(=4-8+6\)
\(=2\)
Both \(a\) and \(c\) have a limit of 2 as \(x\) approaches –2. Because the function \(b\left(x\right)\) lies between \(a\left(x\right)\) and \(c\left(x\right)\), the squeeze theorem dictates that \(\lim_{x \to -2}b(x)\) is also 2.
Carlos is modeling daily average gas prices for the month and determines that the price of gas in dollars for day \(x\) can be represented by some function \(g\left(x\right)\) which lies between the curves \(f\left(x\right)=\sqrt{x+1}\) and \(h\left(x\right)=\frac{1}{6}x+\frac{5}{3}\). Can the squeeze theorem be applied to determine the limit of \(g\left(x\right)\) as \(x\) approaches 8? If so, what is the value of the limit?
The problem states that \(g\left(x\right)\) is a function lying between \(f\left(x\right)\) and \(h\left(x\right)\). So, the first condition of the squeeze theorem is met. The only thing necessary to check is if \(f\) and \(h\) come to the same limit as \(x\) approaches 8. This can be checked by substituting \(x=8\) into each function.
\(f(x)=\sqrt{8+1}=\sqrt9=\pm 3\)
Since we are talking about gas prices, only use the positive value for this limit.
\(h(x)=\frac{1}{6}\left(8\right)+\frac{5}{3}=\frac{8}{6}+\frac{5}{3}=\frac{4}{3}+\frac{5}{3}=\frac{9}{3}=3\)
It is now clear that \(f\) and \(h\) do come to the same limit as \(x\) approaches 8. Therefore, the squeeze theorem can be applied to find the value of \(g(x)\). That limit is the same as \(f(x)\) and \(h(x)\), which is 3.
Eloise is working to determine the effectiveness of her company’s new marketing strategies by plotting revenue by day, where \(x\) represents the days since the new strategies were implemented. She determines that the revenue function \(r\left(x\right)\) is bounded below by the function \(p\left(x\right)=30x+5{,}000\), and bounded above by the function \(q\left(x\right)=\frac{3}{4}x^2+5{,}300\). What is the value of \(\lim_{x \to 20}r(x)\)?
To use the squeeze theorem, \(r\left(x\right)\) must lie between \(p\left(x\right)\) and \(q\left(x\right)\), and \(p\) and \(q\) must have the same limit as \(x\) approaches 20. In this problem, it is given that \(r\) is between \(p\) and \(q\) when the problem states that \(r\) is bounded below by \(p\) and bounded above by \(q\). This means the only remaining condition is checking if \(p\) and \(q\) have the same limit as \(x\) approaches 20. This can be done by substituting \(x=20\) into both functions.
\(p(x)=30\left(20\right)+5{,}000=600+5{,}000=5{,}600\)
\(q(x)=\frac{3}{4}\left(20\right)^2+5{,}300=\frac{3}{4}\left(400\right)+5{,}300=300+5{,}300=5{,}600\)
Because \(p\) and \(q\) have the same limit as \(x\) approaches 20, and because \(r\) lies between them, the squeeze theorem dictates that \(\lim_{x \to 20}r(x)=5{,}600\).
