Solving Optimization Problems

You have likely experienced a situation where you needed to find a balance between two or more variables, in order to achieve an optimal result. Solving these kinds of optimization problems is all about finding the measurements or circumstances that ensure the best, or most efficient, outcome.

In this video, I’m going to show you how to solve these kinds of problems. Let’s get started!

Optimization Problem #1

Suppose a rancher wants to enclose a field on his property for livestock, and he has materials to build 400 meters of fencing. What should the enclosed field’s length and width be in order to maximize the area of the field?

Let’s take a look at some dimension samples and their areas to get a feel for how changing the length and width relates to changes in the area.

One way the rancher could build the fence is with the width of 50 meters and a length of 150 meters. This would use up all 400 meters of fencing.

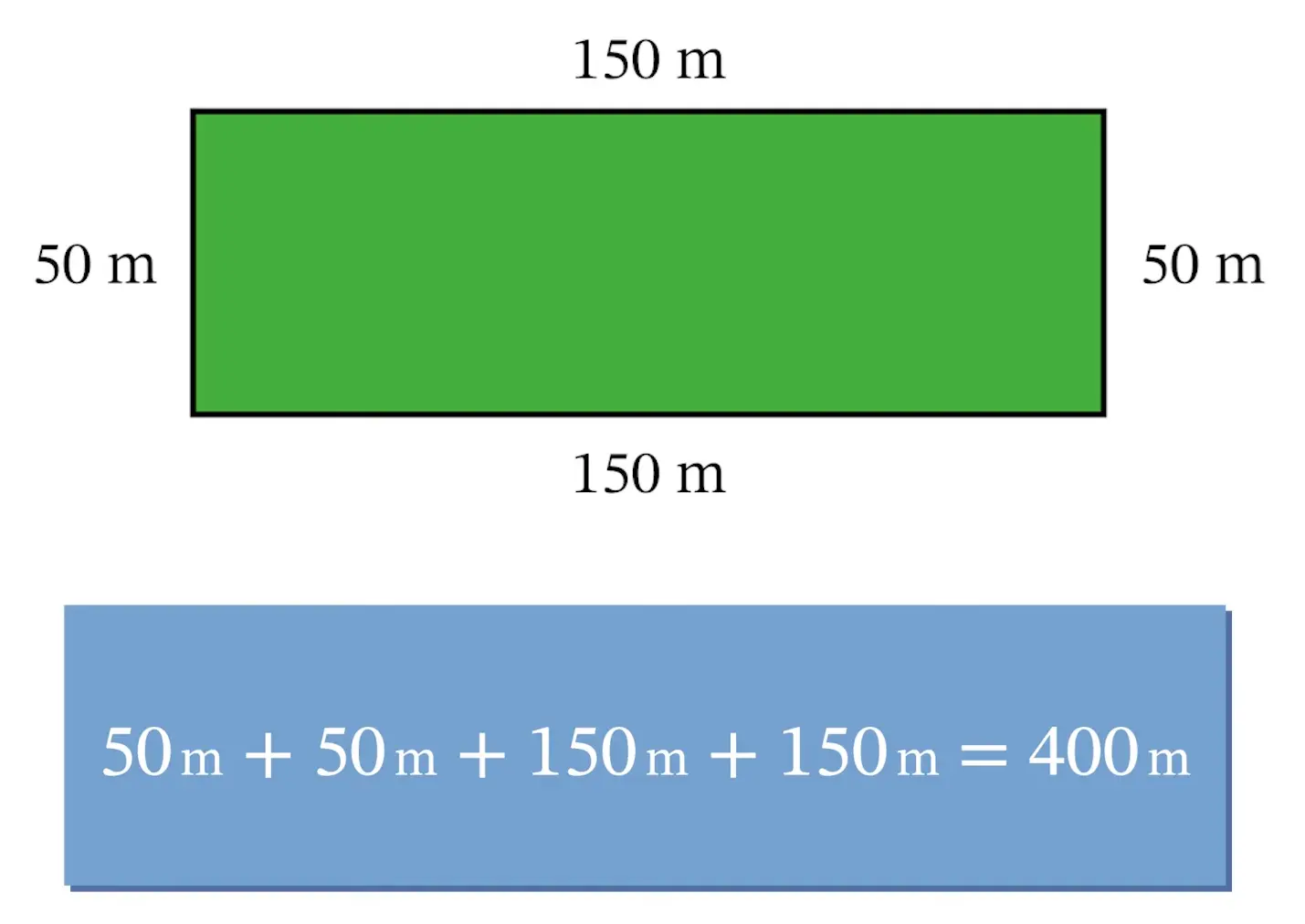
With this setup, the rancher’s field would have an area of $50\times 150=7,500$ square meters.

However, if the rancher chooses to increase the width to 60 meters and therefore decrease the length to 140 meters, the area of the field would then be 8,400 square meters, which is a sizeable improvement!

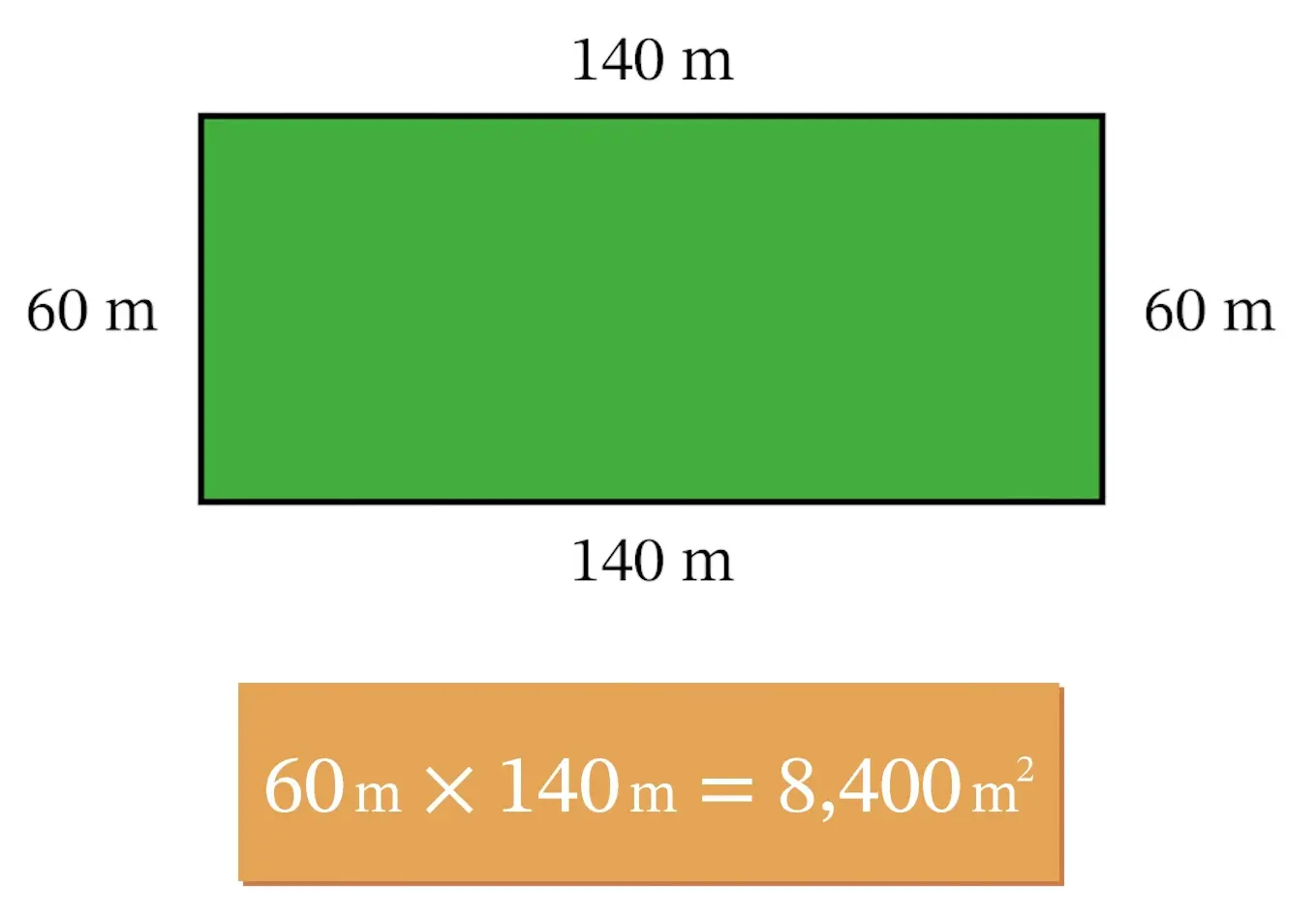
If we keep increasing the width and decreasing the length, we will continue to see the increases in area…up to a point. Eventually, a maximum area will be reached and then the area will begin to decrease. For example, if we increase the width all the way up to 199 meters, and decrease the length accordingly to just 1 meter, the area of the field will only be 199 square meters.

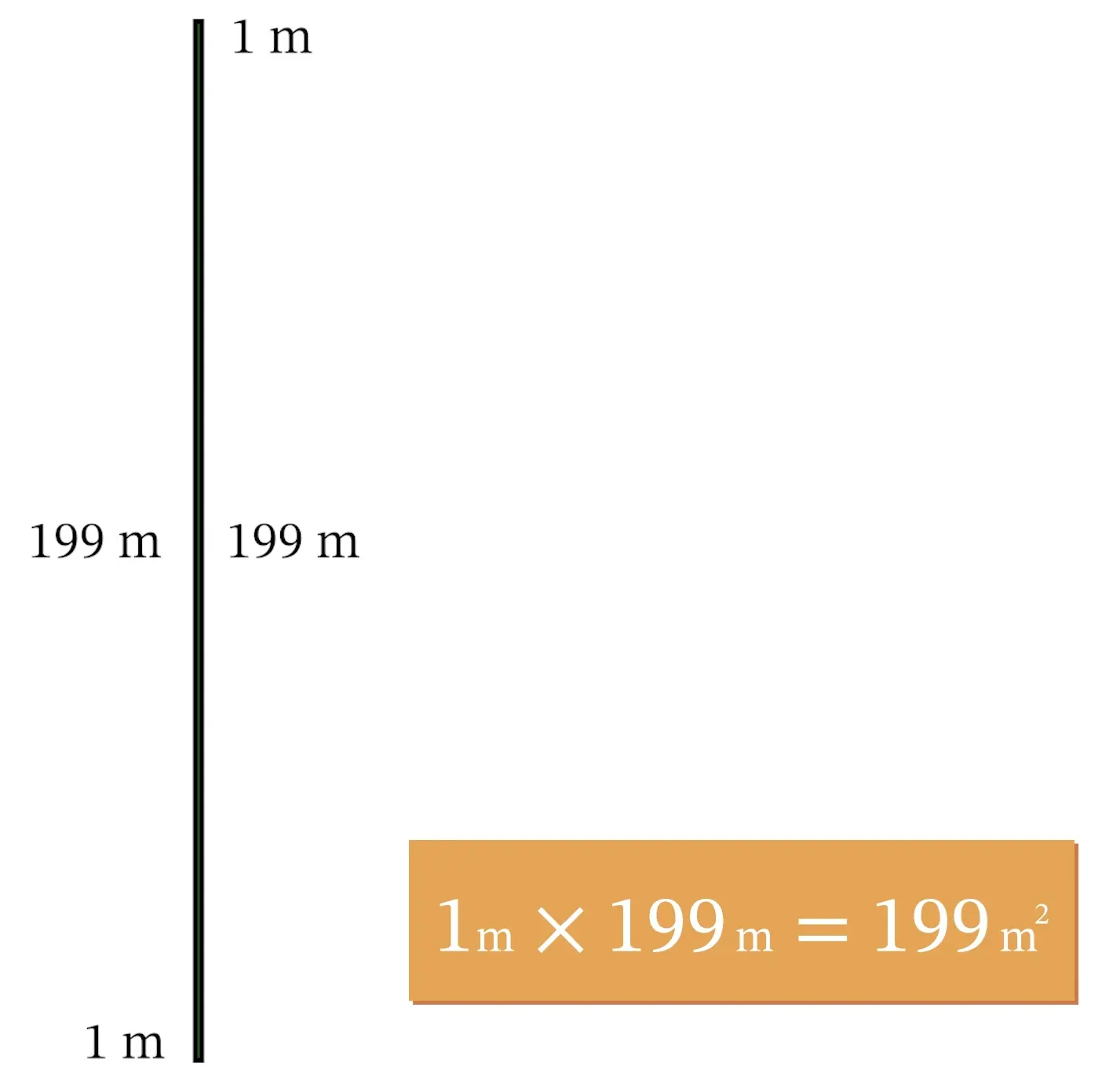
As we can see, the area of the field very much depends on its dimensions, and there should be a “sweet spot,” a set of dimensions which maximizes the area of the field. How can we determine exactly what those optimal dimensions are?

The good news is you won’t need to use trial and error for these problems.

Critical Points

Before we solve this field problem, we need to talk about critical points.

Consider this shape.

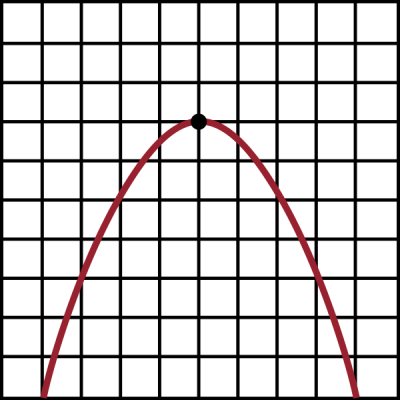
You may recognize this as a parabola, but the important feature to notice is that it has a maximum point. We can see pretty clearly that this is the highest point on the shape, but it also has a special characteristic which makes it what we call a critical point.

What is the slope of the tangent line at this exact point? Since the line is changing directions from upward to downward, the slope at this exact point is zero, and the tangent line is flat.

This would also be true of a minimum point on a curve. At an arc’s lowest point, the line will switch direction from downward to upward and the tangent line will have slope equal to zero.

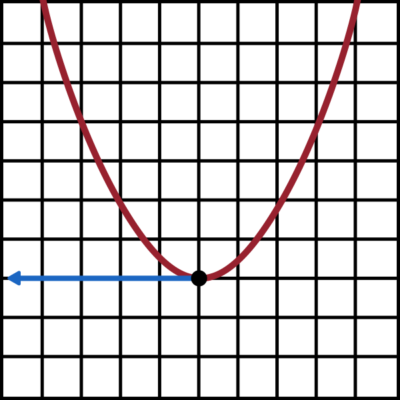
In other words, at these critical points, the value of a function’s derivative equal 0.

Critical points also exist where a function’s derivative does not exist, such as points where there are breaks in continuity or when a function has “sharp” turns.

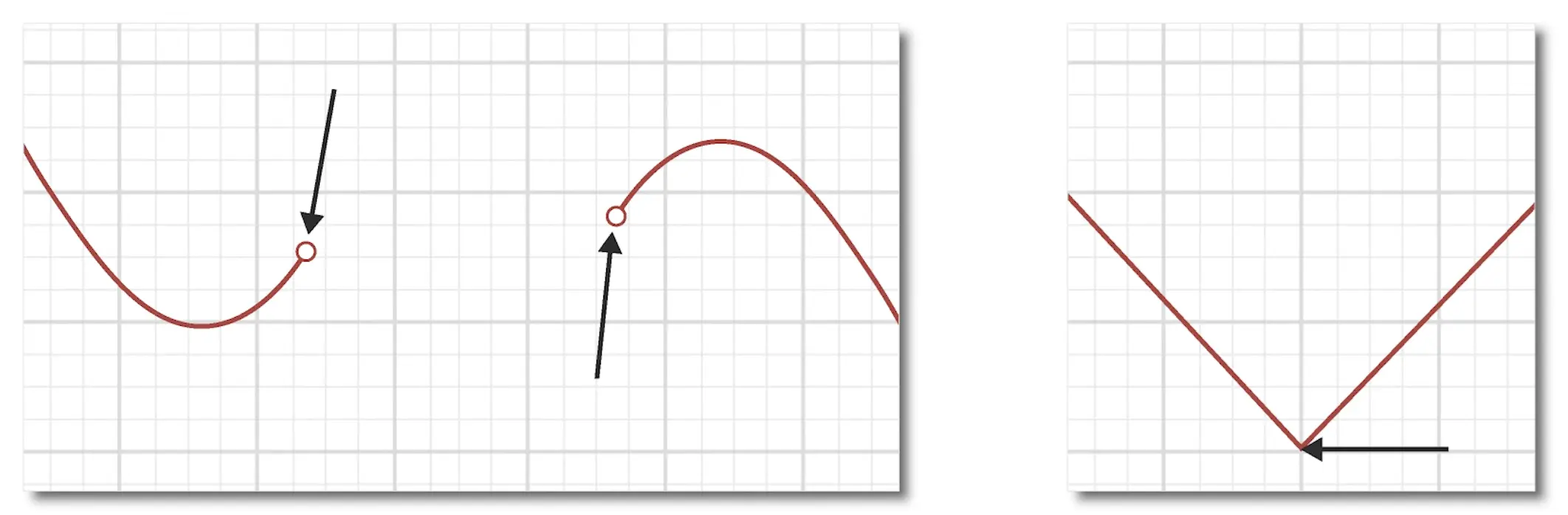
Because of this, we can find minimum and maximum values of a function within particular domains by searching for points where the derivative of the function equals zero or does not exist.

For example, the function $f(x)=-x^2+4x$ is a downward-opening parabola. We can find the maximum of the function by taking the derivative of $f$ and solving for the $x$ value that makes it go to zero or not exist.

Let’s start by taking the derivative of $f$.

 
Since there is no point that would make this undefined, we set $f^{\prime }$ equal to zero and solve for $x$.

 
So the maximum for $f(x)$ occurs at $x=2$. We can then evaluate $f(2)$ to find the height.

 
So this function has a critical point at $(2,4)$.

Let’s return to the example of the rancher now. We know that he needs to use all 400 meters of fencing materials, so the perimeter of the enclosed field must be $2l+2w=400$, where $l$ and $w$ represent length and width respectively.

The area of a rectangle is equal to length times width, but in order to find a critical point, we need to write a function for area in terms of only one variable. Let’s use $l$ as that variable, and we’ll solve for $w$ in terms of $l$ to make the area function.

 
So the area in terms of $l$ is $l\cdot (200-l)$.

 
Simplifying, this equals $200l-l^2$.

Remember, in order to find the dimensions that maximize the field’s area, we need to locate a critical point of this function. Let’s take the derivative of $A$.

 
We can see that $A^{\prime }$ is a linear function. This means it is continuous, and we can solve for where $A^{\prime }$ equals zero.

 
There is a critical point when length of the field is equal to 100 meters, which indicates that the area of the field is maximized when the length equals 100 meters and, consequently, when the width equals 100 meters as well. The area of the field with these dimensions is 10,000 square meters.

Optimization Problem #2

Let’s work through another example. Lisa is working on a geometry project and is making shapes from pliable metal wire. She has 8 feet of wire that she wants to cut into two separate pieces. With one piece she will make a circle, and with the other she will make a square. In order to maximize the total area of the circle and square, how long should the piece of wire for the square be?

Since we are trying to minimize area, we need to come up with a formula for area. This formula needs to be written in terms of only one variable so that we can take its derivative and find a critical point.

Let’s choose the variable to be the letter $x$, representing the length of the wire used for the square. Since the wire is 8 feet long, this restricts the possible values of $x$ to the domain $0\le x\le 8$. We know that the total area must include the circle’s area as well as the square’s, so $A(x)$ will look something like this:

 
The area of a square is equal to its side length squared, and the side length of Lisa’s square will equal one-fourth of $x$. So the square’s area will equal $(\frac{x}{4}{)}^2$, or $\frac{x^2}{16}$.

To get the area of the circle, we need to remember that the length of leftover wire from the square will equal $8-x$ feet. This will make up the circumference of Lisa’s circle. The circumference of a circle equals $2\pi r$, and the area of a circle equals $\pi r^2$.

Let’s get the value of the radius, $r$, by dividing $8-x$ by $2\pi$.

 
Then, we can square this and multiply by $\pi$ to get the circle’s area.

 
Now, we have the formulas for the circle’s area and the square’s area individually. Let’s put them together to get the area function.

Let’s expand the numerator of the first term.

 
To find the derivative of the first term, we could use the quotient rule. However, since the bottom is a constant, we can just factor it out and take the derivative of the top:

Then we can add the derivative of the second term, which is $\frac{x}{8}$.

 
This resulting derivative is a linear function, and we can solve for where it equals 0.

 
Isolate the $x$ terms.

 
Establish a common denominator of $8\pi$.

 
Simplify to find the exact value of $\frac{32}{4+\pi }$, which is approximately 4.5.

 
This indicates that Lisa would cut roughly 4.5 feet for the square, leaving around 3.5 feet for the circle.

Remember, even though we have found this critical point, we also must consider the endpoints of the domain. In this case, we should check $A(0)$ and $A(8)$.

$A(0)$ represents the total area if Lisa uses all the wire for the circle, and this area is approximately 5.093 square feet.

 
$A(8)$ represents the total area if Lisa uses all the wire for the square, and this area is 4 square feet.

 
If Lisa cuts the wire at the critical point, she will have a total area of approximately 2.24 square feet.

 
It seems that Lisa will have the smallest area if she uses the critical point and dedicates about 4.5 feet of wire to the square!

Whenever you see the words “maximize” or “minimize” in a calculus problem, these are signals that indicate an optimization problem is at hand. The first step in solving these is writing a formula for what is being optimized in terms of only one variable. Then, take the derivative, look for critical points, and test these against the endpoints of the domain to find the true maximum or minimum.

This may seem like a daunting process at first, but with some practice you’ll get the hang of it.

That’s all for this review. Thanks for watching, and happy studying!