Simple Machines
Hi, and welcome to this video on simple machines! Today, we’ll talk about some basic types of machines and the physics behind how they work.
Simple machines refers to the most basic set of tools that can be used to facilitate work. When we use a simple machine on an object, we are able to apply a force over a distance in order to achieve a greater force over a shorter distance. So, the simple machine enables us to exert a force that we may not be able to exert otherwise.
Before we get any further, let’s remember that work is defined by a force multiplied by the distance over which the force is applied,
\(W=Fxd\)
Energy is always conserved, so when we put some amount of work into a simple machine, we are actually still getting that same amount of work out of the machine (assuming no energy is lost in friction). In other words,
\(W_{in}=W_{out}\)
Then, we can substitute in \(Fxd\) for the input and output work.
\(F_{in}d_{1}=F_{out}d_{2}\)
\(F_{in}\) is the force we apply to the machine, \(d_{1}\) is the distance over which we apply that force, \(F_{out}\) is the force the machine applies to the load we are moving, and \(d_{2}\) is the distance over which the machine applies the force. The important concept here is that, while the amount of work isn’t changing, the force applied by us can be different from the force on the load, as long as the distances are different.
From this idea, we get the concept of mechanical advantage, or MA.
\(MA=\frac{f_{out}}{F_{in}}=\frac{d_{1}}{d_{2}}\)
The mechanical advantage is a ratio that describes how much the machine amplifies the force you are putting into it. So, MA > 1 is what we are looking for in a machine, which means the machine is increasing the force.
Now let’s look at some examples of these simple machines!
There are considered to be six different types of simple machines: the lever, the pulley, the inclined plane, the wheel and axle, the wedge, and the screw. It may not be obvious how the input and output forces work in each of these machines, so let’s take a closer look at each type.
LEVER
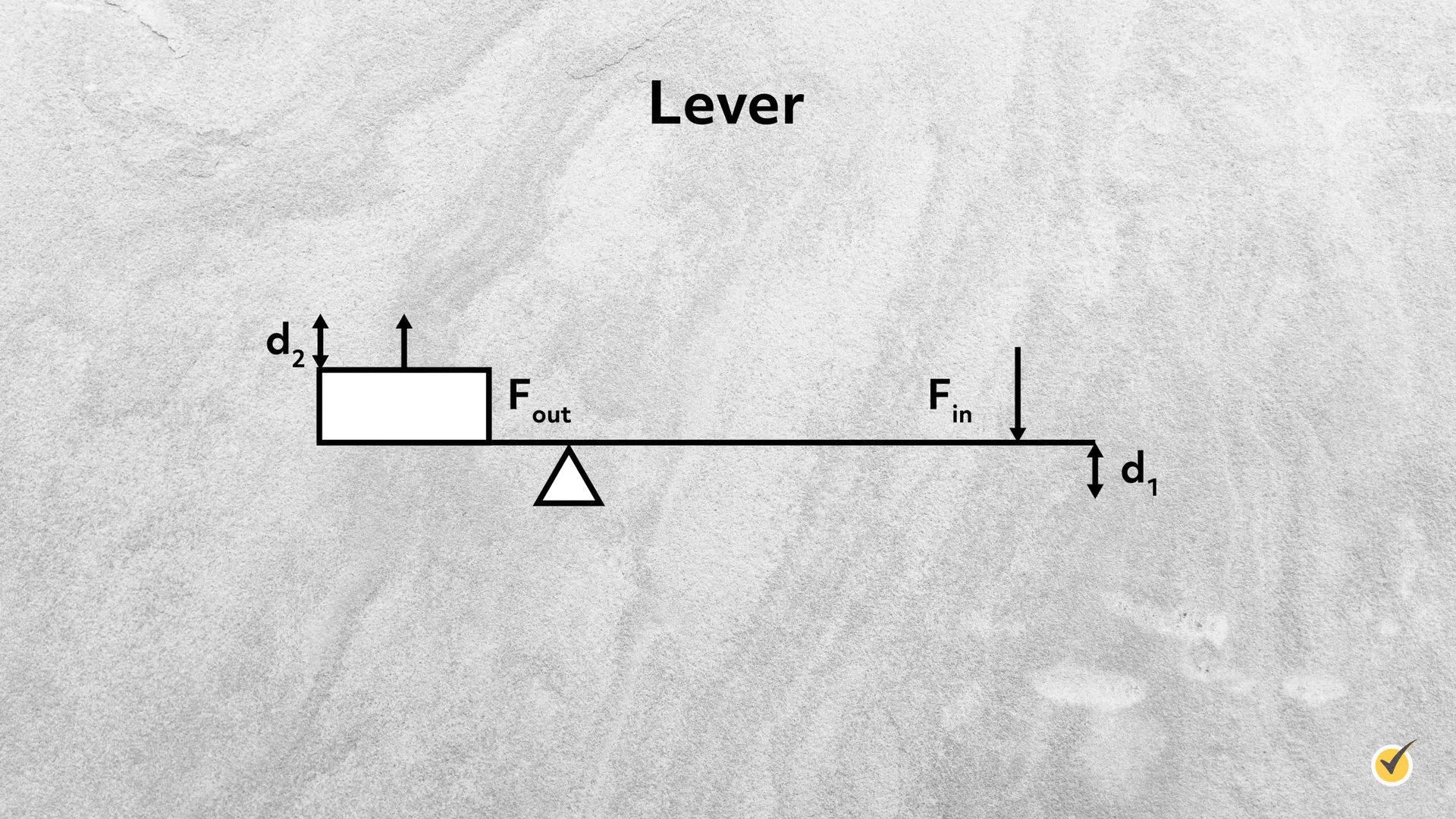
A lever is essentially any long board or rigid device with a pivot point, or fulcrum. The object or load that you want to do work on is at one end of the lever and you exert a force at the opposite end. The distances that each end moves up or down are \(d_{1}\) and \(d_{2}\).
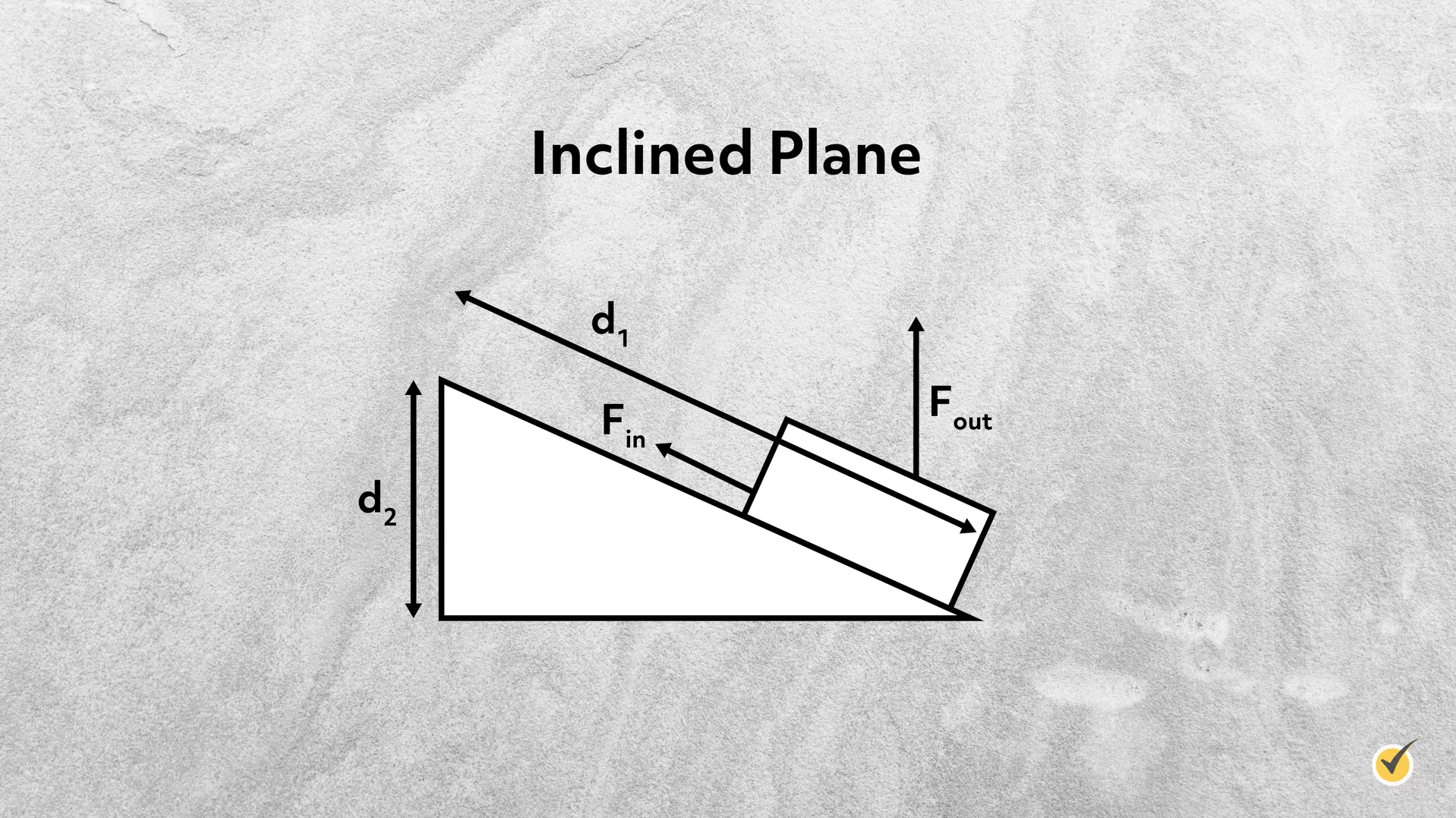
INCLINED PLANE
An inclined plane is simply a ramp that can be used to move an object a certain vertical distance using less force than if you were to directly lift up. In the case of an inclined plane, the plane isn’t necessarily moving anything itself, but it provides a means for you to push or pull an object to that vertical distance more easily. Here, \(F_{in}\) and \(d_{1}\) are directed along the plane, while \(F_{out}\) and \(d_{2}\) are along the vertical distance the object has moved.
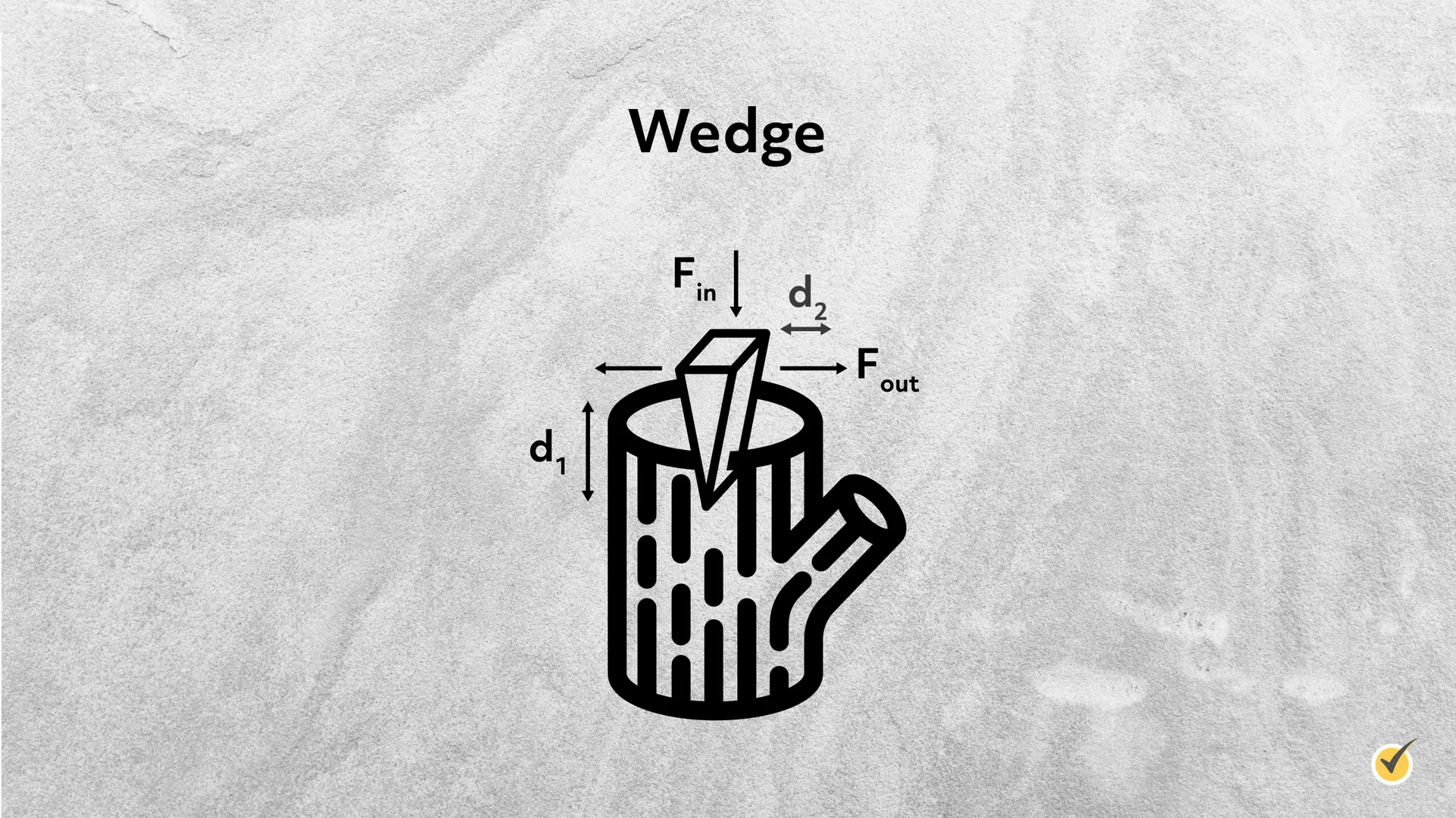
WEDGE
A wedge is a simple machine that is often used to pry something apart or to cut it into two pieces. An axe is a great example of a wedge. The input force is directed downward into the crack (think of how you apply the force on a knife when chopping food) and the distance is simply how far in you push the wedge. The output force is the force pushing the two pieces apart and the distance is how far apart the two pieces have been displaced.
WHEEL AND AXLE
A wheel and axle is a slightly more complicated type of lever, where the ratio of distance to the force that is applied is proportional to the radii of the wheel \((r_{wheel})\) and the axle \((r_{axle})\). For the mechanical advantage, we can use
\(MA=\frac{F_{out}}{F_{in}}=\frac{r_{wheel}}{r_{axle}}\)
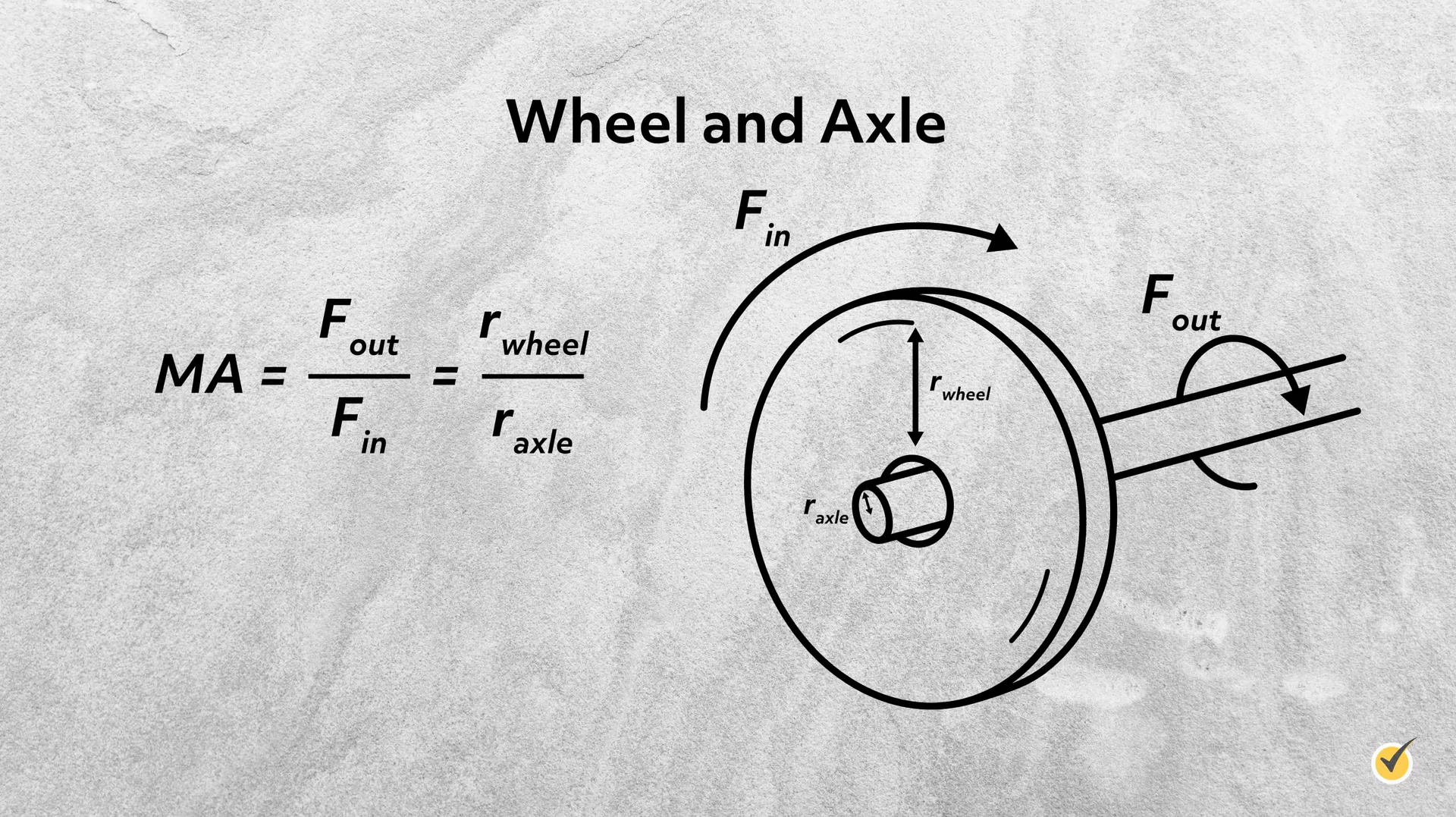
The (smaller) input force is applied to the wheel, which has a larger radius and diameter, while the (larger) output force is exerted by the axle, which has a smaller radius and diameter.
PULLEYS
There are a few different types of pulleys, but all involve one or more wheels with a rope set in a groove along the diameter of the wheel. The load you are trying to move is attached to one end of the rope, while the input force is exerted (the rope is pulled) at the other end. For a simple, one-wheel pulley system, the magnitude of the input and output force are actually equal. However, the pulley system allows you to apply a force in a different direction to move the load. Think about a well with a pulley system at the top and a rope attached to a bucket of water. While you still have to exert a force equal to the weight of the bucket \((\text{ weight}=\text{ mass}\times{ gravity}\) here) along an equal distance that the bucket has moved, the direction you are pulling the rope is likely different than the vertical motion of the bucket, thus making it easier to retrieve the bucket.
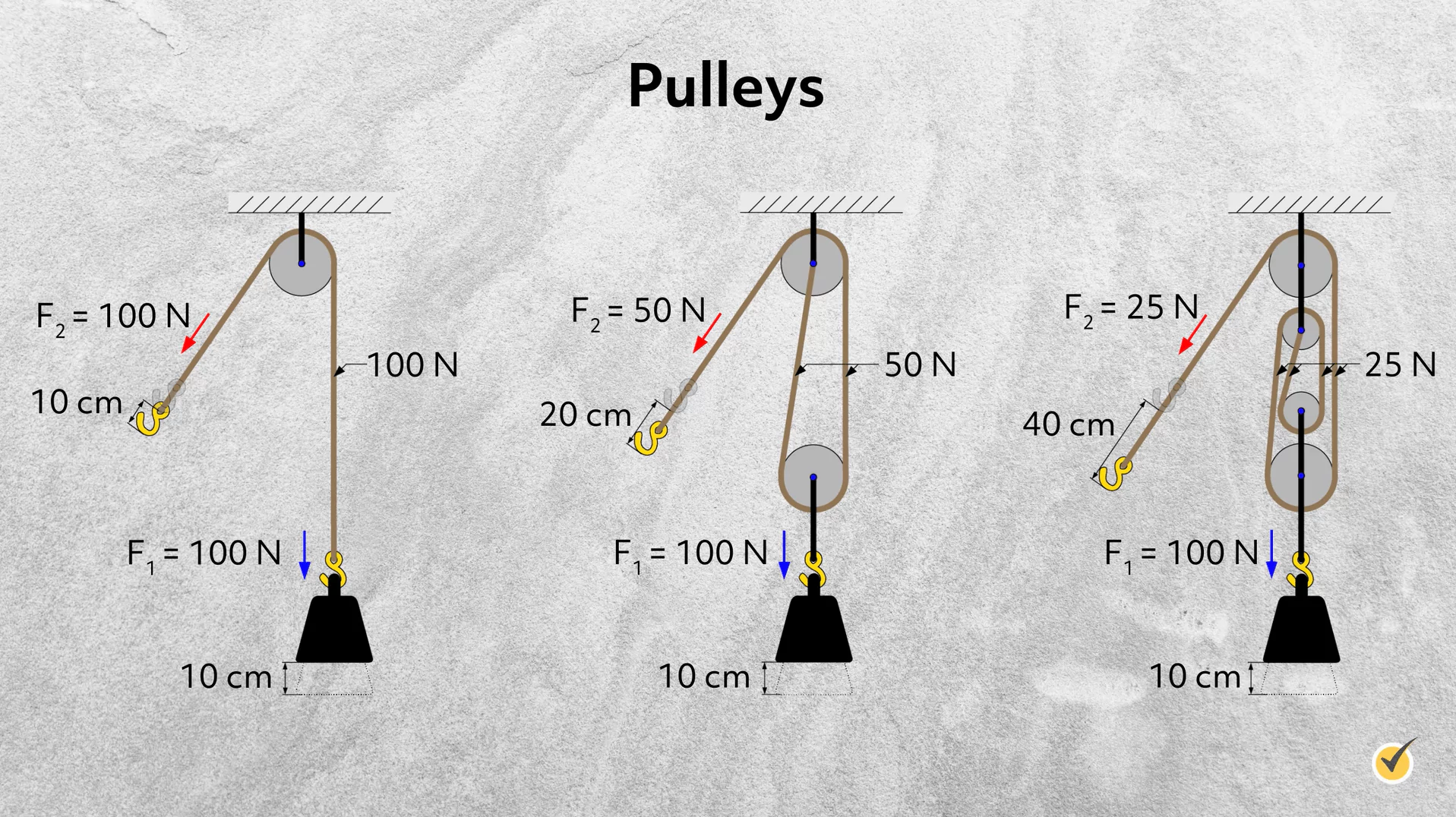
Of course, this kind of system may not always be useful. That’s why many pulley systems are composed of more than one pulley, which allows the distances and forces to vary, therefore increasing the mechanical advantage.
Here, you can see how the input force \((F_{2})\) decreases as more pulleys are added to the system, while the load mass (and force) stay the same. Luckily, the mechanical advantage is simple to calculate for these systems. It is simply equal to the number of pulleys in the system!
SCREWS
Screws are actually just inclined planes wrapping around a kind of cylinder. These include traditional screws used in woodwork, bottle caps, and various screws used in machinery.
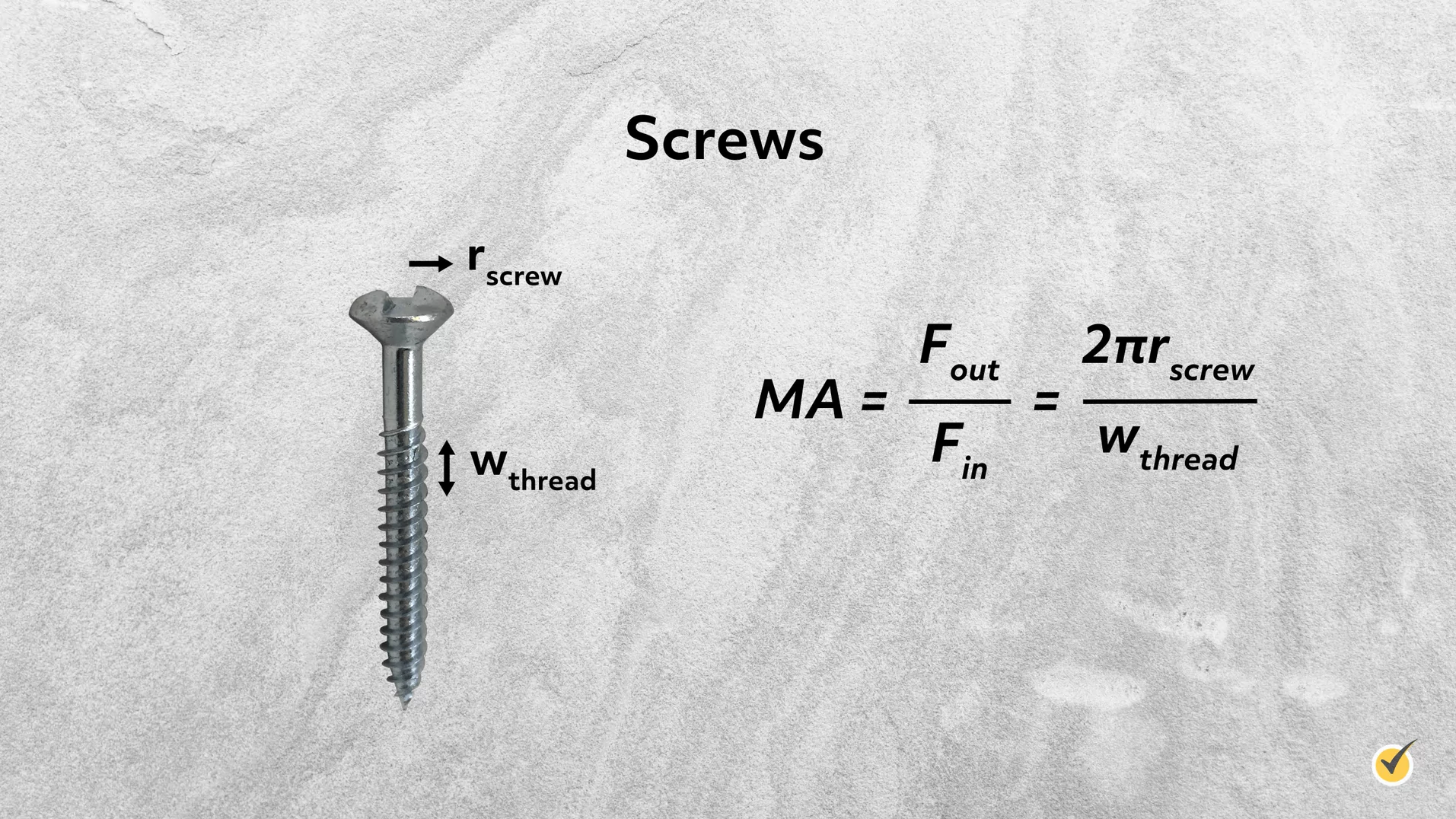
The forces and distances occur in a circular motion with screws, so the mechanical advantage looks a little different than with a regular inclined plane. However, every time a screw is turned 360°, it penetrates the material by the width of the thread of the screw, \(w_{thread}\). This can be thought of as the distance associated with the output force, \(F_{out}\), while the circumference (\(2πr_{screw})\) of the screw can be thought of as the distance associated with the input force, \(F_{in}\), since we must turn the screw by that amount to get the screw to go in by a thread width. So the mechanical advantage is
\(MA=\frac{F_{out}}{F_{in}}=\frac{2\pi r_{screw}}{w_{thread}}\)
Now that we’ve gone over the physics behind simple machines, let’s test your knowledge with some questions!
1. If you apply a force of 12 N to one end of a lever and the resulting force on the object at the other end is 20 N, will the object move the same distance that you applied the 12N force?
- No, it will move a longer distance.
- No, it will move a shorter distance.
- Yes, it will be the same distance.
- There’s no way to know without knowing the distance you moved it.
2. How can you increase the mechanical advantage of a system of pulleys?
- Increase the length of the rope.
- Increase the mass of the load.
- Add additional pulleys to the system.
- You cannot increase the mechanical advantage.
That’s all for this review of simple machines. Thanks for watching, and happy studying!