Shape of Chemical Bonds

The geometry of a molecule is directly linked to the shape of bonds between the atoms that comprise that molecule. That geometry, in turn, influences many of the molecule’s fundamental properties, such as reactivity, polarity, phase equilibria, magnetism, and biological activity. The first step in understanding bond shapes and molecular geometry is the application of Lewis theory. This theory is used to define the Lewis electron dot structure, also called the Lewis structure, of a compound. A Lewis structure identifies a molecule’s bonding electron pairs and its lone electron pairs. This information allows us to predict and picture (in a simplistic way) the number of bonds formed between atoms in a molecule. The second step in determining bond shapes is to apply valence-shell electron-pair repulsion theory, or VSEPR theory, to the Lewis electron dot structure. This process allows us to determine a very good approximation of the molecular geometry of a compound solely based on its molecular formula.
Octet Rule
A key principle guiding both Lewis structures and bond geometry is the octet rule. Basically, the octet rule describes the tendency for atoms to have eight electrons in their valence shells. When atoms have less than eight valence electrons, they tend to react with other atoms to form more stable molecules. This process involves some atoms sharing electrons with other atoms to result in more atoms with a filled outer shell. The sharing of electrons is the basis of covalent bonding. An atom will continue to form bonds (that is, grab and share electrons from neighboring atoms) until it has an octet of electrons (in other words eight electrons) in its outer shell.
Lewis Structures
In Lewis structures, unpaired electrons are dots, and bonding electrons are lines between atoms. To properly construct a Lewis structure, there are several steps:
1. The total number of electrons that will be accounted for in the structure is determined by summing the number of valence electrons for each atom in the molecule and then subtracting the molecule’s charge from this sum. For example, the carbonate ion has 22 valence electrons and a molecular charge of \(–2\). So, the total number of valence electrons is 24. – – — –
C (4 valence electrons)
O (6 valence electrons per oxygen atom \(\times\) 3 oxygen atoms per molecule = 18)
Total = 22 valence electrons – (–2) for the molecule charge = 24 valence electrons
2. Draw the general form of the molecule structure connecting the central carbon atom with the oxygen atoms as a single line. The single line represents a bond formed by the sharing of electrons. So, for the carbonate ion example, we would have this.
3. Add the nonbonding electron pairs (the valence electrons that are not shared with other atoms) as dots around each atom until their octet is full. Remember that every single bond involves, or counts as, two electrons. For the carbonate ion, this step can be depicted like this.
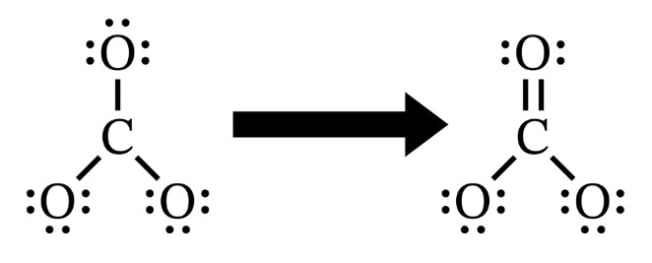
4. If we run out of valence electrons by using all of them to fill the octets of the oxygen atoms before the central atom’s octet is filled, we must add a double bond to the structure. A double bond indicates sharing of two sets of electron pairs between the central atom (carbon in our example) and the outer atoms (oxygen in our example).
For example, the carbonate ion has 24 valence electrons (from step 1), and all of these are accounted for in filling the oxygen octets. Note on the structure that we have three sets of lone electron pairs around each oxygen and one single bond connecting to the carbon atom. This accounts for all 24 valence electrons, but the carbon octet isn’t full because it only shares two electrons with each oxygen (as indicated by the single bonds). Therefore, to bring the carbon octet up to eight electrons, we have to force one of the oxygen atoms to share two sets of electrons with the carbon. This is a double bond and is represented by two parallel lines. Note how the double bond replaces the lone electron pair on the top oxygen atom. The double bond thus accounts for a total of four electrons.
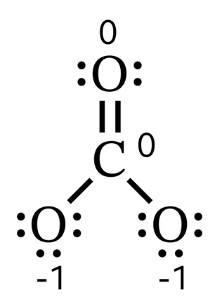
5. Calculate the formal charges for each of the atoms in the molecule. This formula is used to determine the formal charge:
For example, the formal charge for each of the single-bonded oxygen atoms of the carbonate ion is \(6–1–6=–1\). The double-bonded oxygen and the carbon atom both have formal charges of zero. Therefore, the carbonate ion has an overall charge of \(–2\) (since it has two single-bonded oxygen atoms).
Formal charges allow us to represent the spatial distribution of electrostatic charge on a Lewis structure (see example showing charge distribution on carbonate structure)). This information is used to determine the polarity of the molecule.
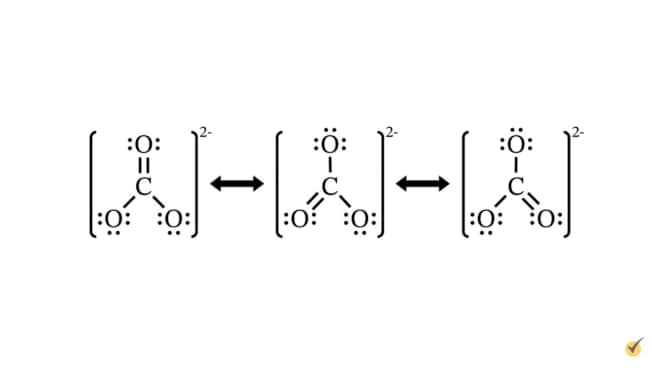
Resonance structures
Single Lewis structures can be too simplistic to fully describe the bonding in some types of molecules and ions. This is due to the delocalization of electrons. The bonding in such molecules can usually be represented using resonance structures. These are sets of two or more Lewis structures that define the possible atomic bonding relationships for a molecule or ion. For example, there are three possible choices of how to arrange the bonding within the carbonate ion. None of these structures describes precisely how bonds are arranged within the molecule, but together they give the range of possibilities.
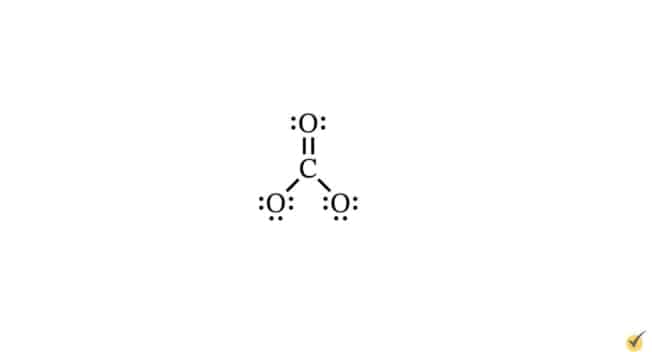
Molecular Geometry
Lewis dot structures can be combined with VSEPR theory to determine the angles formed between pairs of bonds. VSEPR theory quantifies how electron groups repel each other. An electron group consists of all electrons (bonding and non-bonding) distributed around a given atom in a molecule. These can be lone electron pairs or single-, double-, or triple-bonded electrons. For example, in our carbonate ion, we can see three electron groups around the central carbon atom. Two of these groups are single bond pairs, and one is a double bond.
On the other hand, a water molecule has four electron groups around the central atom: two lone electron pairs and two single bond pairs.
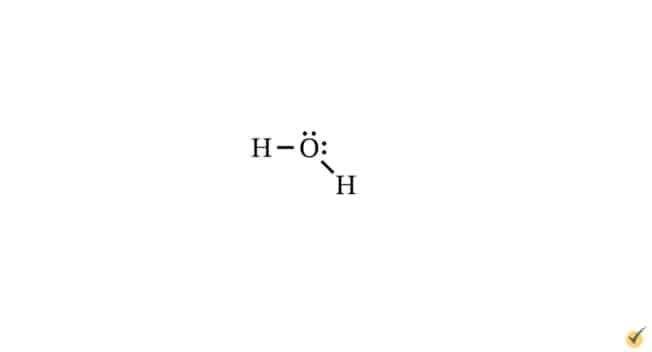
According to VSEPR theory, electrostatic repulsion causes electron groups to spread as far away from each other as geometrically possible. This process is key in determining bond shape and, thus, molecular geometry. This is because atoms and electrons of a molecule arrange themselves to minimize electrostatic repulsion and maximize attraction. In this way, the bond shapes and molecular geometry represent a kind of equilibrium state with the lowest possible energy for the system. For instance, the angle between each of the bonds in a carbonate ion is 120o.
There are two ways of quantitatively describing the shape of bonds and molecules. One is the electron-group geometry, and the other is molecular geometry. Both of these are dealt with in VSEPR theory. There are five electron groups, each of which is defined by the number of electron groups in the molecule. These are summarized in this table.
| Electron Groups in Molecule | Electron Group Geometry |
|---|---|
| 2 | Linear |
| 3 | Trigonal-Planar |
| 4 | Tetrahedral |
| 5 | Trigonal-Bipyramidal |
| 6 | Octahedral |
The molecular geometry of a compound depends on both its number of electron groups and its number of lone electron pairs. The different molecular geometry types and their ideal bond angles are summarized here. Ideal bond angles give a good estimate for the angle, but the exact angle can be a few degrees different depending on other more complicated factors.
| Electron Groups in Molecule | Electron Group Geometry | Lone Electron Pairs | Molecular Geometry | Ideal Bond Angles (degrees) | Example Compound |
|---|---|---|---|---|---|
| 2 | Linear | 0 | Linear | 180 | Carbon Dioxide \(CO_{2}\) |
| 3 | Trigonal-Planar | 0 | Trigonal Planar | 120 | Carbonate (\(CO_{3}^{2-}\))  |
| 1 | Angular | 120 | Ozone (\(O_{3}\) | ||
| 4 | Tetrahedral | 0 | Tetrahedral | 109.5 | Sulfate (\(SO_{4}^{2-}\))  |
| 1 | Trigonal Pyramidal | 109.5 | Hydronium (\(H_{3}O_{+}\))  | ||
| 2 | Angular | 109.5 | Water (\(H_{2}O\)) | ||
| 6 | Trigonal-Bipyramidal | 0 | Trigonal Bipyramidal | 90, 120 | Phosphorus pentafluoride (\(PF_{5}\)) 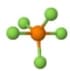 |
| 1 | Seesaw | 90, 120 | Tellurium tetrachloride \(TeCl_{4}\) 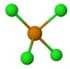 | ||
| 2 | T-shaped | 90 | Chlorine trifluoride (\(ClF_{3}\)) | ||
| 3 | Linear | 180 | Triiodide ion (\(I_{3}^{-}\))  | ||
| 5 | Octahedral | 0 | Octahedral | 90 | Hexafluorophosphate (\(PF_{6}^{-}\)) 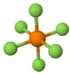 |
| 1 | Square Pyramidal | 90 | Antimony pentachloride \(SbCl_{5}^{2-}\)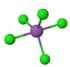 | ||
| 2 | Square Planar | 90 | Xenon tetrafluoride \(XeF_{4}\)  |
Review
The shapes of bonds determine the molecular structure of compounds. Bond shapes and molecular structures can be represented using a combination of Lewis electron dot structures and valence-shell electron-pair repulsion theory. The Lewis structure schematically represents the distribution and sharing of electrons (bonding) within a molecule. VSEPR theory determines the bond shapes and molecular geometry type.
Before we go, let’s tackle a couple of review questions.
1. What is the main force that determines the shape of bonds and, thus, the geometry of molecules?
The electrostatic repulsion of electrons determines the shape of bonds. A molecule’s lowest energy state (that is, the most stable geometry) is one in which repulsive forces between atoms are minimized.
2. Look at the Lewis structure for the ammonia molecule.
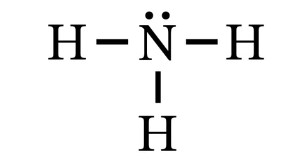
- How many lone electron pairs are present?
- How many electrons are involved in bonding?
- How many electron groups are there around the nitrogen atom?
- Using the bond table we showed previously, determine the electron group geometry and molecular geometry of this molecule.
- The two dots indicate one lone electron pair on the nitrogen atom.
- There are six electrons involved in bond formation. Every single line involves the sharing of two electrons between the nitrogen atom and a hydrogen atom.
- There are four electron groups around the nitrogen atom: three single bonds and a lone electron pair.
- Since there are four electron groups, this molecule is classified as having a tetrahedral electron group geometry. And since there is one lone electron pair, its molecular geometry is trigonal pyramidal.
That’s all for this review. Thanks for watching and happy studying!