Position, Velocity, and Acceleration

Imagine you are at a red light. After a few seconds, the light turns green and you begin to speed up in the car. Whenever we speed up, we can feel ourselves get pushed into our seats a bit. Whenever you feel that push, it means you are accelerating!

Acceleration occurs when you pick up speed, and your acceleration is a measure of how quickly you’re gaining speed. Speed is a similar word to velocity. The difference between speed and velocity is that speed is how fast an object is moving, or changing position, and velocity is how fast that object is moving and in what direction. Position tells us the location of an object. In this video, we are going to talk about how acceleration, velocity, and position are all related to each other, as well as some applications of this knowledge that help scientists in the real world!

Imagine you are in a car that is traveling at a constant speed of 60 miles per hour down a long, straight highway. After one hour, you will have traveled 60 miles. After a second hour, you’ll have gone 120 miles; after a third hour, 180 miles; and so on. We can get an idea of this movement graphically by plotting miles against hours, like this:

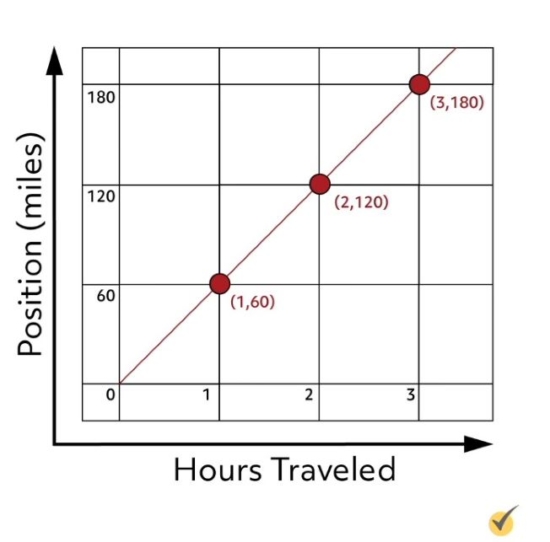
Then, we can connect the dots to make a line. Another way we could describe this line is “miles traveled as a function of time.”

The height of this line at a given positive x-value, or time value, tells us how far the car has driven from the starting point. This is why such a line is often referred to as a “position function.” The slope of this line is unsurprisingly 60, since the line rises by 60 units for every horizontal unit. Because the slope is 60, and we know that the car is moving at a speed of 60 miles per hour, we can understand that the slope of the position function gives us the car’s velocity.

This concept can even be applied when a position function is not a straight line. For example, if a tire starts rolling down a hill and has the position function \(y=x^{2}\), where \(x\) represents seconds passed, and \(y\) represents feet traveled, then we can find the tire’s velocity at any given time by finding the slope of the position function at that time.

From our study of calculus so far, we understand that “slope” is often a keyword for derivative problems. So it should come as no surprise that the quickest way to find the velocity of an object from its position function is by taking the derivative of that position function!

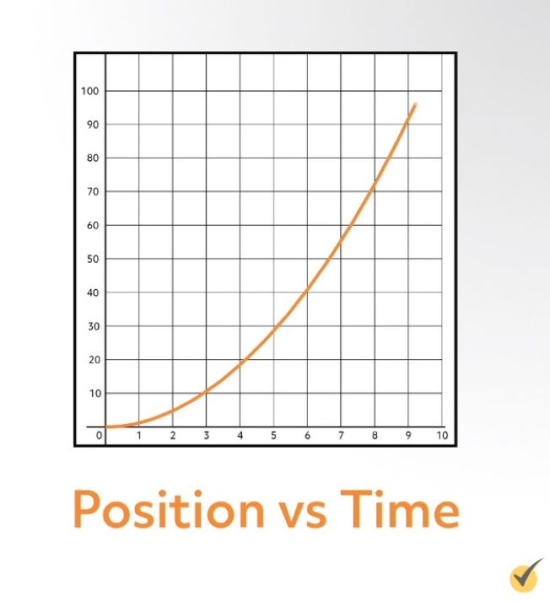
In the case of the tire rolling downhill, its velocity is equal to the derivative of \(x^{2}\), which is \(2x\).

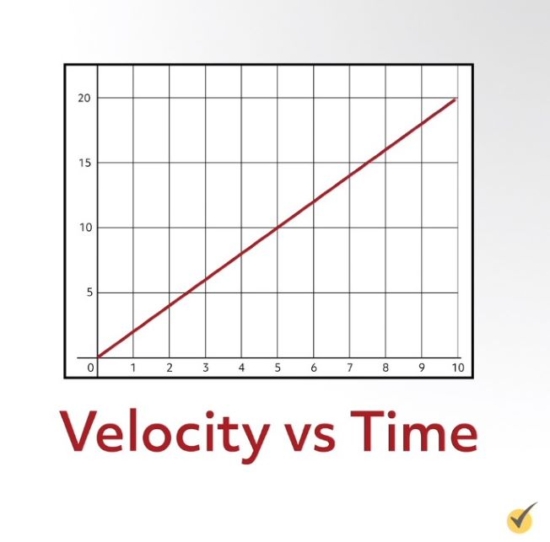
Once you have taken the derivative to acquire the object’s velocity function, you can plug in any \(x\)-value, or time value, to get the value of the velocity at that exact moment. For example, after 5 seconds, the tire has a velocity of 10 feet per second.

Remember how we talked about acceleration in the beginning of this video? Acceleration is a measure of how velocity changes. Since velocity is a measure of how position changes, and we can find velocity by taking the derivative of the position function, it may come as no surprise that we can find the acceleration by taking the derivative of the velocity function!

So since the tire has a velocity function \(v(x)=2x\), its acceleration function is equal to the derivative of \(2x\), which is 2.

The unit for the tire’s acceleration is feet per second squared, because we are considering how the velocity (in feet per second) is changing (per second).

So if you have the velocity function of an object, you can take its derivative to find the acceleration function! Similarly, if you have an object’s position function, you can use derivatives to find both its velocity and acceleration functions.

Let’s try an example. Joseph launches a model rocket with an altimeter on it to record its height during flight. Once the rocket returns to the ground, Joseph determines that the height of the rocket, in meters, is given by the function \(h(t)=-4.5t^{2}+90t\), where t is seconds after liftoff.

Find the velocity function of the rocket, and determine at what time velocity equals zero. Then find the acceleration function of the rocket, and determine what the acceleration is at \(t=2\) seconds.

First, we need to find the velocity function of the rocket. To do this, we just need to take the derivative of its position function (which in this case is the height function \(h(t))\).

So velocity equals \(-9t+90\) meters per second at \(t\) seconds. Now we want to know at what time velocity equals zero. To do this, all we need to do is set \(-9t+90\) equal to 0, then solve.

So at exactly 10 seconds after liftoff, the rocket has a velocity equal to zero. This is where the rocket reaches its highest point and is about to fall back toward the ground.

Next, we need to know the rocket’s acceleration function. Since acceleration can be found by taking the derivative of the velocity function, we know that:

So the acceleration of the rocket equals \(–9\) meters per second squared. Since this is a constant value, it doesn’t change from one second to another. The acceleration of the rocket at 2 seconds is then still equal to \(–9\).

Whenever you have an object’s position function, you can easily find its velocity function by taking the derivative of the position function. By extension, you can also find an object’s acceleration function by taking the derivative of its velocity function. And to find the object’s position, velocity, or acceleration at a specific time, just plug that time into the respective function and simplify.

I hope that this video was helpful. Thanks for watching, and happy studying!