Newton’s Law of Gravitation

In 1686, Sir Isaac Newton published Principia Mathematica in which he presented his Law of Universal Gravitation. The word “universal” here is important because he was presenting a law that would work both on the Earth and in space. He had the idea that the same force that governed the way apples fall from a tree was responsible for the way the Moon orbits around the Earth. This went against the philosophy of the time, which said that space was perfect and “heavenly” and composed of entirely different materials than those found on the Earth. Isaac Newton was relying on work done by Galileo Galilei, who used a telescope to show that places in space such as the Moon were just like the Earth. Newton used physical laws to further unify the realms of Earth and space.

Newton’s Law of Universal Gravitation

Newton’s Law of Universal Gravitation, often referred to simply as “the law of gravity,” says that two things that have mass are attracted to each other by a natural force which Newton chose to call gravity. This force between these two things is proportional to the product of their masses. That means that larger masses have stronger force. For instance, if you hold your hands next to each other, there is a gravitational force between your hands. You will not feel this force because it is so tiny. However, on the scale of large masses such as the Moon and the Earth, the force is commensurately massive.

Mathematics Behind Gravity

In addition, the force is inversely proportional to the square of the distance between the two masses. That means that the farther two masses are from each other, the weaker the force between them will be. To be more specific, if two objects are moved twice as far from each other, the force of gravity gets four times smaller. If the objects move three times further from each other, the force of gravity gets nine times smaller. The important concept here is the realization that as objects move away from each other, the force of gravity between them gets small very quickly.

This law is usually shown not in words but in the form of this mathematical equation. In this equation, \(F\) is the force of gravity, and \(G\) is a constant called the gravitational constant, which means it’s always the same. The value of \(G\) is \(6.67\times 10-^{11}\). The \(m\)’s in the equation are the masses of two objects. For instance, if we were to find the force of gravity between the Earth and the Moon, one of the masses in the equation would be the Earth’s and one would be the Moon’s. Typically, the larger object gets assigned the uppercase M and the smaller object gets the lowercase \(m\), but mathematically, it doesn’t matter which goes where. The \(D\) refers to the distance between the centers of the two objects. If you drop a ball on the surface of the Earth, the distance in this equation would be from the center of the ball to the center of the Earth. Because the Earth is so large and, for most humans, the ball is never very far above the surface of the Earth, when this equation is applied to objects falling near the surface of the Earth, the radius of the Earth is usually used as the distance.

Prior to Newton’s formulation of gravity, Galileo had discovered that two objects with different masses fall to the Earth at the same speed. A myth claims Galileo dropped two balls off the Leaning Tower of Pisa, though he likely never went to such lengths. Instead, he used wooden balls that he was able to open and place different weights inside of, and then rolled these balls down ramps. He was not able to explain why balls with different masses finished their race at the same time. It may seem like this experiment shows that Newton’s law of gravity does not work! After all, we just said that larger masses produce larger forces. However, as we will see, this observation matches what we should expect to see when we combine Newton’s law of gravity with his laws of motion.

For instance, if you have a bowling ball falling to the Earth, the masses you would use in the gravity equation are the masses of the bowling ball and the Earth. If you drop a baseball instead, the masses you would use are the mass of the baseball and the mass of the Earth. The bowling ball, with a larger mass, feels a larger gravitational force. It is absolutely true that, when you drop a bowling ball and a baseball, the bowling ball feels more force from the Earth than does the baseball. It is also true that these two balls hit the ground at the same time. This result is consistent with Newton’s Second Law of Motion, which says that the force required to move an object is equal to the mass of the object times its acceleration.

In this case, the mass would be the mass of the bowling ball and the force would be the force between the bowling ball and the Earth. This force is given by Newton’s Law of Gravity.

Because the mass of the bowling ball, denoted by the lowercase m, shows up on both sides of the equation, we can divide both sides by this mass and it will completely disappear from the equation. Then, we find that the acceleration of the bowling ball is given by a single formula.

The acceleration of the bowling ball depends on the gravitational constant, the mass of the Earth, and the distance between the bowling ball and the center of the Earth, which we have discussed is essentially the radius of the Earth. These values are the same for any object near the surface of the Earth. Therefore, the acceleration due to gravity for any object near the Earth’s surface is the same. If we put in the values, we find that this acceleration equals nine-point-eight meters per second squared, or thirty-two feet per second squared.

This value is used so often that it is given its own symbol: a lowercase \(g\), called “little \(g\).” Notice that “little \(g\)” is different from the gravitational constant \(G\).

One of the experiments astronauts from Apollo 15 did on the Moon was a demonstration of dropping a hammer and a feather to show that they landed at the same time. You may try this yourself and find that it doesn’t work! For two objects with different shapes and masses here on Earth, air resistance will be a factor. That’s why Galileo used identical balls with different masses, and why the Moon, which has no atmosphere, is an ideal place to test this theory.

Now a concept that takes some time to get used to is distinguishing between weight and mass. Weight is not the same thing as mass. One way to think of it is that your mass is related to how much of you there is and your weight is related to where you are. In other words, your weight is a measure of the force with which the Earth is pulling on your mass. If you were to travel to the Moon, your mass would stay the same, but because the Moon has less mass than the Earth, the force between you and the Moon would be less than the force between you and the Earth. This means you would weigh less on the Moon. You can actually use Newton’s Law of Universal Gravitation to find out what your weight would be on different planets, moons, and other celestial bodies.

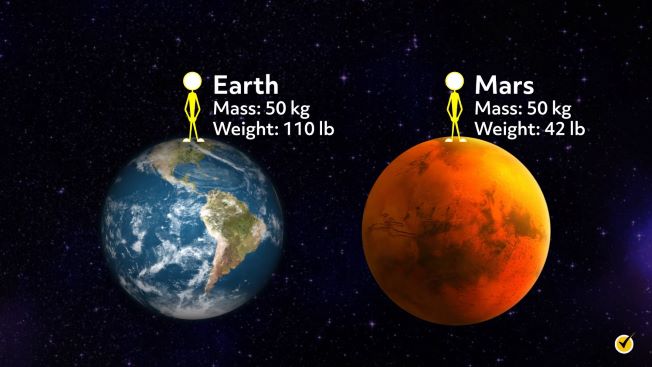
However, it is important to remember that distance is also part of the equation. In other words, just because an object is more massive doesn’t mean that you would experience more weight. A great example of this is Saturn. Saturn doesn’t actually have a surface for you to stand on, but let’s imagine that it does. Saturn has a much larger mass than the Earth, but it also has a larger radius. If you could stand on the “surface” of Saturn, you would actually weigh almost the same as you do on the Earth.

Newton’s Law of Gravity is a useful tool for determining the force between two objects based on their masses and the distance between them. However, Newton’s Law of Gravity is incomplete! It does a great job describing the motion of pretty much everything we see and interact with on a daily basis, so what’s missing? Mathematically, Newton’s Law of Gravity is an approximation, albeit a very good one for most everyday-scale applications. Even the astronauts only needed to use Newton’s Laws to get to the Moon. But, Newton only codified the motion that he observed and defined equations to predict future observations; he didn’t explain why gravity exists. Einstein sought to do that in 1933 when he published his Theory of General Relativity. In that paper, he said that mass sits in a four-dimensional space-time fabric, and that mass warps the fabric of space-time. This warped space-time is what we perceive as gravity.

As far as we know, Einstein’s conception of gravity is completely correct. Of course, people thought that was true for Newton’s Law of Gravity for two hundred years as well. Science never stops bringing surprises.

That’s all for this review. Thanks for watching, and happy studying.