
Hi, and welcome to this video on the multiplication rule of probability!
To refresh your memory, probability is a measure of how likely it is that a given event will occur.
Whether you realize it or not, you use probability every single day to make choices and decisions in your daily life. For example, if you wake up to an 80% chance of rain, you are very likely to bring along an umbrella with you to work. A pitcher facing a batter with a .347 batting average is likely to pitch carefully and strategically.
An “80% chance of rain” is another way of saying that out of 100 days with this particular weather pattern, 80 will likely have rain. A .347 batting average indicates that the batter will get a hit 347 out of 1,000 at-bats, on average.
Those are just the probabilities of one event occurring. To determine the likelihood of multiple events occurring, we need to use the multiplication rule of probability. To understand this rule, we’ll need to dive deeper into the realm of probability.
Independent and Dependent Events
First, it is important to distinguish between independent and dependent events.
Two events are independent of each other if the occurrence of the first one does not have any impact on the second. As an example, a coin can be flipped twice, but no matter what side appears after the first flip, the second flip still has a 50/50 chance of landing on either heads or tails.
In contrast, say you were making two selections from a standard deck of cards and picked an ace on the first selection without returning it back into the deck. The probability for your second selection has changed because you now have one less card in the deck. These two selections would be dependent since the first one had an impact and made a difference for the probability of the second selection.
With this background, let’s dig deeper and explore another element of probability—what if you wanted to determine the probability of two events occurring in a sequence?
Determining the Probability of Multiple Events
Example 1
As an example, say you had a traditional six-sided die and wanted to determine the probability of rolling a 2 on the first roll, AND a 3 on the second roll.
Since each number appears only once on the die, we know that the probability of rolling a 2 is 1 out of 6. Remember, since the numbers of the die do not change no matter how many times it is rolled, the rolling of dice would be considered independent events. Therefore, the probability of rolling a 3 on the second roll is also 1 out of 6.
But how do we figure out the probability of BOTH of these events occurring? To answer this question, we utilize the multiplication rule of probability.
This rule states that if you want to find the probability of both event A and event B occurring, you would multiply the probability of event A and the probability of event B.
In our example, event A would be the probability of rolling a 2 on the first roll, which is \(\frac{1}{6}\). Event B would be rolling a 3 on the second roll, the probability of which is also \(\frac{1}{6}\).
Therefore, to find the probability of both of these events occurring, we would take the probability of event A and multiply it by the probability of event B.
Multiplying the numerators will give us 1, and multiplying the denominators will give us 36, giving us an answer of 1 over 36.
This means that, in all likelihood, a person will roll a 2 followed by a 3 once in every 36 attempts.
Example 2
Let’s consider another example.
Say you had a standard deck of cards and wanted to determine the probability of first drawing the king of hearts, and after which drawing any card in the suit of hearts.
Let’s go through this problem one event at a time.
The first event is drawing the king of hearts. We know there are 52 cards in a standard deck, and there is only one king of hearts in every deck. Therefore, the probability of drawing a king of hearts is \(\frac{1}{52}\).
Now let’s consider the second event—drawing one of the remaining cards in the suit of hearts. Remember, the second event is a dependent event. That means that it must reflect the changes in circumstances caused by the first event.
Here’s what I mean: Normally there are 13 cards of every suit in the deck. But since we already pulled out the king of hearts, there are only 12 cards in the suit of hearts left. If we are writing our probability in the form of a fraction, that would give us 12 in our numerator, for the 12 remaining hearts.
And while there are normally 52 cards in a standard deck, since we have already taken out one card, there are only 51 cards remaining. That gives us 51 in our denominator and a probability \(\frac{12}{51}\) for the second event.
Following the rule of multiplication, we would multiply \(\frac{1}{52}\) and \(\frac{12}{51}\).
Multiplying the numerators would give us 12, and multiplying the denominators, 52 and 51, would give us 2,652, leaving us with a probability of \(\frac{12}{2,652}\). Since both the numerator and denominator are even numbers, we know they can be simplified, at least by dividing both by 2.
In this case, we can actually divide both by 12, giving us a final answer of \(\frac{1}{221}\). This means that the probability of drawing the king of hearts, followed by another card from the suit of hearts, would be once in every 221 attempts.
So remember, to determine the probability of multiple events occurring, just multiply the probability of event A and the probability of event B, simplifying your fractions when possible.
I hope this review was helpful! Thanks for watching, and happy studying!
Multiplication Rule of Probability Practice Questions
Which scenario describes two independent events?
Dependent events describe situations where the first event has a direct affect on the second event. For example, if you park illegally, the result is that you will likely get a ticket. The first event has an effect on the second event. Only one scenario provided is an example of independent events. Planting a flower garden does not depend on whether or not you own a dog. The two events are independent of each other.
Determine the probability of rolling a six on a standard dice, and then rolling a five.
When determining the probability of two or more events, the probability of the first event can be multiplied by the second event. In this example, the probability of rolling a six is \(\frac{1}{6}\), and the probability of rolling a five is also \(\frac{1}{6}\). The multiplication rule of probability states that \(\frac{1}{6}\times\frac{1}{6}\) will be the probability of both events occurring: \(\frac{1}{6}\times\frac{1}{6}=\frac{1}{36}\)
Determine the probability of spinning an odd number, and then spinning a number greater than seven.
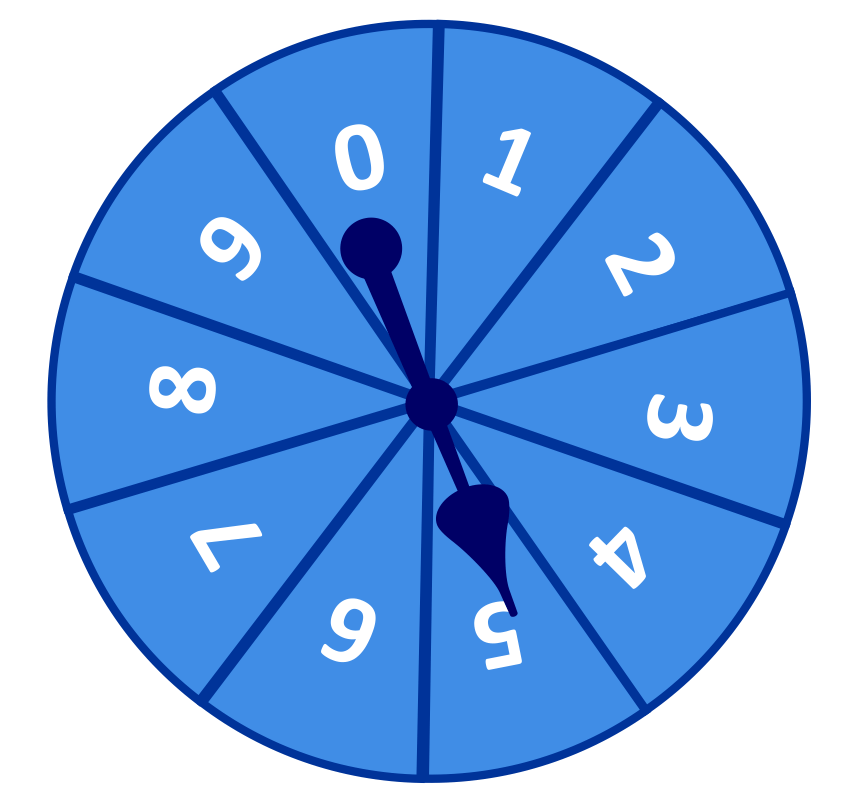
The multiplication rule of probability can be used to solve this problem. The probability of spinning an odd number is \(\frac{5}{10}\), and the probability of spinning a number greater than seven is \(\frac{2}{10}\). When these two probabilities are multiplied, we see that our answer is \(\frac{10}{100}\), or in simplest form \(\frac{1}{10}\).
In a classroom of 30 students, 8 students are in Art Club, 12 students are in Drama Club, and 17 students are in Soccer. What is the probability of randomly selecting a student that is involved in Drama Club?
There are 12 students in Drama Club, and there are 30 students in all. This means that 12 out of 30 students are in Drama Club. This fraction represents the probability \(\frac{12}{30}\), or in simplest form, \(\frac{2}{5}\).
A bag contains 20 marbles. 12 marbles are red, and 8 marbles are green. The marbles are not replaced after they are selected from the bag. What is the probability of selecting a red marble, and then a green marble?
The multiplication rule of probability can be used to solve this problem. The probability of selecting a red marble is \(\frac{12}{20}\). This marble is not replaced into the bag, so now the probability of selecting a green marble is \(\frac{8}{19}\). When these two probabilities are multiplied we get \(\frac{96}{380}\), or in simplest form \(\frac{24}{95}\).