Matrices – Data Systems
A matrix is commonly defined as a rectangular array of numbers, symbols, or expressions arranged in rows and columns. Matrices can be added, subtracted and multiplied and they can be manipulated in order to discern certain characteristics. However, they can also be representative of data and used in linear algebra applications.
A common representation of matrices is that of data tables. Suppose the owner of a burger chain wants to see cumulative data from three locations. Matrices could be used like this:
Since the dimensions of all three matrices are equal and the data in each corresponding entry represents the same quantity, i.e., the data in the row 1 column 1 entry is always June burgers, etc., these matrices can be added or subtracted as needed.
Matrices can also be used to solve systems of linear equations. This method is parallel to the classic elimination method. Using that method, we can add equations together and multiply equations by scalars in order to isolate and solve for the different variables. If this sounds familiar, it should, because those are also the legal row operations when working with matrices.
Let’s look at the steps involved, then we’ll look at a system in action.
- For all equations in the system, put the terms in the same variable order (for example x, y, z)
- Create a matrix using just the coefficients of the terms in the equations in the system. Put a 0 placeholder where variables don’t exist in an equation.
- Augment the matrix with a constant matrix comprised of the solutions to the equations in the system.
- Use row operations to get the matrix into reduced row echelon form.
- Read off the solutions.
The vertical line inside the matrix is often used to show augmentation. When augmenting with a vector composed of the solutions to the equations in the system, it’s also a nice equal sign placeholder. It’s time to row reduce.
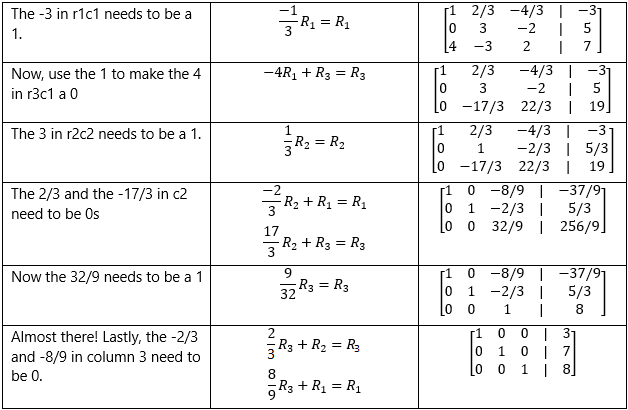
Now that our matrix is fully row reduced, all we need to do is read off the numbers. The matrix now tells us that:
The solution to the system might be written as (3,7,8).
Note that you don’t necessarily need to do the full row reduction in order to solve the system. For example, in the second to last step, the matrix says that:
\(\left\{\begin{matrix}
x-\frac{8}{9}z=\frac{-37}{9}\\
y-\frac{2}{3}z=\frac{5}{3}\\
z=8
\end{matrix}\right.\)
Knowing the value of z lets you substitute it into the other equations to figure out the values of x and y.
The example system is an independent system because there is only one solution. Matrices can show dependent systems (infinite solutions, i.e. the same line) and inconsistent systems (no solution) as well.
If you are row reducing a matrix representing a system and create a zero row, then you have a dependent matrix. This is comparable to using substitution or elimination and ending up with 0=0.
If you are row reducing a matrix representing a system and you create a zero row that has a nonzero number as the last entry, then you have an inconsistent matrix. This is comparable to using substitution or elimination and ending up with 0=some number.
Thanks for watching, and happy studying!
Matrix Practice Questions
A matrix is an array of numbers organized into _______ and _______.
matrices and columns
zeros and ones
rows and columns
systems and quadratics
A matrix is a rectangular array of numbers. The numbers are called elements, or entries. Matrices have a wide application in engineering, economics, and physics.
Which item below shows the system of linear equations as a coefficient matrix?
\(\begin{cases}3x+2y-z=1\\x-2y+z=0\\2x+y-32z=-1\end{cases}\)
The terms are already in the same variable order \((x,y,z)\) so the coefficient matrix can be created using just the coefficients of the terms.
Which of the following matrices are in row echelon form?
For a matrix to be in row echelon form, the following characteristics need to be present:
The values on the diagonal need to be ones.
The values below the ones need to be zeros.
The other values can be any number.
These three characteristics are found only in matrix B.
Write the matrix in row echelon form.
\(\left[\begin{matrix}1&2&4\\2&2&7\\3&6&8\end{matrix}\left|\,\begin{matrix}1\\3\\-1\end{matrix}\right.\right]\)
In order to write this matrix in row echelon form, we need the numbers along the main diagonal to be 1.
We also need the numbers below the main diagonal to be 0.
When these two requirements have occurred, the matrix will be in row echelon form.
Getting the numbers below the main diagonal to be 0:
The process is similar to the process of elimination. Let’s multiply the entire first row by -2, and then add this to row two to create a new row two. When row one is multiplied by -2, and then added to row two, the new row two becomes: \(\left[\begin{matrix}0&-2&-1\end{matrix}\left|\,\begin{matrix}1\end{matrix}\right.\right]\)
Now let’s work on row three. This time let’s multiply the entire original row one by -3. The new row one becomes \(\left[\begin{matrix}-3&-6&-12\end{matrix}\left|\,\begin{matrix}-3\end{matrix}\right.\right]\). Now add this to row three which is \(\left[\begin{matrix}3&6&8\end{matrix}\left|\,\begin{matrix}-1\end{matrix}\right.\right]\). The result is \(\left[\begin{matrix}0&0&-4\end{matrix}\left|\,\begin{matrix}-4\end{matrix}\right.\right]\) for the new row three.
At this point the matrix shows:
\(\left[\begin{matrix}1&2&4\\\mathbf0&-2&-1\\\mathbf0&\mathbf0&-4\end{matrix}\left|\,\begin{matrix}1\\1\\-4\end{matrix}\right.\right]\)
The zeros are in the correct places, so let’s move on to the ones. The 1 in the first row is already in the correct place, which is helpful.
Getting the main diagonal numbers to be 1:
Let’s divide row two by -2. Row two was \(\left[\begin{matrix}0&-2&-1\end{matrix}\left|\,\begin{matrix}1\end{matrix}\right.\right]\), and after dividing this row by -2 it becomes \(\left[\begin{matrix}0&1&\frac{1}{2}\end{matrix}\left|\,\begin{matrix}-\frac{1}{2}\end{matrix}\right.\right]\). Now we can deal with row three. Divide row three by -4. Row three was \(\left[\begin{matrix}0&0&-4\end{matrix}\left|\,\begin{matrix}-4\end{matrix}\right.\right]\) and now it becomes \(\left[\begin{matrix}0&0&1\end{matrix}\left|\,\begin{matrix}1\end{matrix}\right.\right]\).
Now the matrix shows:
\(\left[\begin{matrix}1&2&4\\0&1&\frac{1}{2}\\0&0&1\end{matrix}\left|\,\begin{matrix}1\\-\frac{1}{2}\\1\end{matrix}\right.\right]\)
We did it! The matrix is in row echelon form.
Find the solutions for the system of equations. The row echelon form of the matrix is provided.
System of equations:
\(\begin{cases}4x−2y−5z=−51\\4x−y−2z=−36\\4x−2y+4z=−24\end{cases}\)
Reduced row echelon form:
\(\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\end{matrix}\left|\,\begin{matrix}-6\\6\\3\end{matrix}\right.\right]\)
The matrix is fully row reduced. This allows us to see the solutions for x, y, and z.
Row one is \(\left[\begin{matrix}1&0&0\end{matrix}\left|\,\begin{matrix}-6\end{matrix}\right.\right]\), which means that \(x=-6\).
Row two is \(\left[\begin{matrix}0&1&0\end{matrix}\left|\,\begin{matrix}6\end{matrix}\right.\right]\), which means that \(y=6\).
Row three is \(\left[\begin{matrix}0&0&1\end{matrix}\left|\,\begin{matrix}3\end{matrix}\right.\right]\), which means that \(z=3\).