
Hi, and welcome to this video on linear equations! Today, we will be looking at what linear equations are and how to solve systems of linear equations.
Reviewing Linear Equations
Before we dive in, let’s quickly review what a linear equation is.
Remember that a linear equation describes a straight line on a graph. They generally look something like this: \(y=mx + b\). The slope of the line is represented by \(m\), and the \(y\)-intercept is represented by \(b\). \(x\) and \(y\) simply represent an ordered pair that would fall on the graphed line for that equation.
Here is an example of a linear equation and the graph to match.
Remember that slope represents rise over run. So a slope of positive 3 represents a rise of 3 and a run of 1 (up 3 and over 1).
This example was already set up in what’s called slope-intercept form. However, not all of the linear equations you work with will be conveniently set up this way. Sometimes you will need to manipulate the equation in order to get it into slope-intercept form. This process needs to occur before you can begin graphing.
Inverse Operations
It’s important to remember that when you are solving for variables within a linear equation, the objective is to use inverse operations in order to isolate each variable. For example, if you were solving for \(y\) in the equation \(4=-2x+y\), the process would look like this.
In order to isolate the variable \(y\), we need to get rid of the term \(-2x\). To do this, we use inverse operations. The inverse of negative \(2x\) is positive \(2x\). So we add \(2x\) to both sides and we get \(2x+4=y\). If we reverse our equation we get \(y=2x+4\).
Now the linear equation is in slope-intercept form (\(y=mx+b\)). It is now graphable because we have isolated the variable \(y\).
Solving Systems of Linear Equations
Now that we’ve reviewed linear equations, we can dive into the process of solving what we call systems of linear equations.
By “system”, we just mean more than one equation. When we want to solve for a system of equations, we are essentially looking for the point of intersection when the equations are graphed. We have solved the system when we can locate the point where the lines meet.
For example, the solved system for the linear equations \(x-2y=-2\) and \(3x-2y=2\) would look like this:
Both equations are graphed, and the lines intersect at the point \((2,2)\). That means that the ordered pair \((2,2)\) is our solution for the system of equations.
Graphing
The three common strategies that are used to solve systems of linear equations are graphing, substitution, and elimination.
Let’s focus first on the graphing method. This method has three main steps.
- Step 1 is to manipulate both equations so that they are in slope-intercept form (\(y=mx+b\)).
- Step 2 is to graph both equations.
- Step 3 is to identify the ordered pair where the lines intersect.
Let’s take a closer look at these three steps with an example.
We’re going to use the system \(y=-3x-7\) and \(y=x+9\).
Remember, to solve this system, we need to figure out where the lines intersect when they’re graphed.
Let’s try the three steps together.
Step 1 is to manipulate the equations so that they are both in slope-intercept form. For this example, both equations are already set up in this form, so we are ready for step 2.
Step 2 is to graph both equations. Let’s look at the first equation \(y=-3x-7\). The value \(-3\) represents the slope of the line, and the value \(-7\) represents the y-intercept. With these two pieces of information we are able to build a line.
Now let’s graph the second equation on the same coordinate grid.
Now we have both equations graphed, so we’re ready for Step 3. Let’s locate the ordered pair where the lines meet. The graphing method is a convenient strategy visually, because we can see exactly where the lines cross. We can clearly see that the lines intersect at the point \((-4,5)\) so the solution for this system of linear equations is \((-4,5)\).
Let’s try a tougher example where the equations are not already given to us in slope-intercept form. For this example we’ll use the system \(3x-y=4\) and \(7x+2y=18\).
First, we need to manipulate both equations so that they are in slope-intercept form. Let’s start with the first one:
We need to isolate the variable \(y\). So first we’re going to subtract \(3x\) from both sides. This gives us \(-y=-3x+4\).
Right now we have \(-y\). The negative in front of the \(y\) is essentially a \(-1\times y\). We need to get rid of that negative 1 by doing the inverse. This means that we need to divide both sides of the equation by negative 1. \(-3x\) divided by negative 1 gives us \(3x\), and 4 divided by negative 1 gives us negative 4. So \(y=3x -4\). Now \(y\) is on its own, and the first equation is in slope-intercept form, so it’s graphable.
Now let’s isolate the variable \(y\) in the second equation so that we can graph both lines together. First, we’re going to subtract \(7x\) from both sides. That gives us \(2y=-7x+18\), and we’re going to divide by 2 on both sides. This leaves us with \(y=-\frac{7}{2}x+9\). We can also write it this way: \(y=-3.5x+9\).
At this point, we have two equations that are both in slope-intercept form:
Equation 1: \(y=3x-4\)
Equation 2: \(y=9-3.5x\)
Now we just need to graph both lines and determine where the lines intersect. Here is what our graph will look like.
The system of linear equations is solved when you can identify the ordered pair where the lines intersect. We can see that the lines meet at \((2,2)\).
If you are working to solve a system and the graphed lines end up being parallel, never intersecting, then the system has no solutions. Similarly, if you graph a system and the lines completely overlap each other, then the system has infinite solutions.
Substitution
The graphing method is often a really convenient way to solve systems. However, sometimes it can be more efficient to solve systems using the substitution or elimination method. These two methods use more of an algebraic approach. Let’s first take a look at the process for using the substitution method.
For this example we’ll use the system \(3x + 5y = 13\) and \(2x + y = 4\).
The second equation appears to be easier to solve for \(y\), so let’s solve for \(y\) by using inverse operations and subtracting \(2x\) from both sides. So this gives us \(y=-2x+4\). This is step 1.
Step 2 is when we take this value of \(y\), which is \(-2x+4\), and we plug it into the \(y\) of our other equation (equation 1). This is the substitution process. So we have \(3x+5\times -2x+4=13\).
Now step 3, solving for \(x\). You will use the distributive property and inverse operations to solve for \(x\). First, distribute the 5, multiplying it by \(-2x\) and 4. From here we have \(3x-10x+20=13\).
Now combine your “like terms”. \(3x-10x\) gives us \(-7x+20=13\). Now we’re going to subtract 20 from both sides. This gives us \(-7x=-7\). Now we divide both sides by negative 7 and get \(x=1\).
We’re halfway there! Now we just need to use this value of \(x\) to solve for \(y\). Here’s step 4. We know that \(x=1\), so let’s plug this in for \(x\) in the equation \(y=-2x+4\).
So we have \(y=-2\times 1+4\). Now we’re going to simplify. So \(y=-2+4=2\). Now we see that \(y=2\). So the solution for this system of equations is \((1,2)\).
Elimination
Another way to solve systems of equations is using what’s called the elimination method. For this method, you first need to manipulate the equations so that the variables are on one side, and the constants are on the other.
Let’s use the systems \(x =y+5\) and \(3x+2y=5\) for this equation.
Using inverse operations, the first equation becomes \(x-y=5\) and the second equation looks ready to go as is. Now all of the variables are on one side, and the constants are on the other. The objective of the elimination method is that when you add or subtract the two equations, one of the variable terms will be completely cancel out, leaving us with a much easier equation to solve. For example \(5x\) would cancel out with \(-5x\).
Let’s look closely at both equations. Remember, we are going to be choosing whether to add or subtract both equations, with the goal of eliminating one of the variable terms. Eliminating a variable term simply means having a coefficient of zero.
Notice that if we multiply all parts of our first equation by 2, the term negative y would become negative 2y. This is helpful because this negative 2y will cancel out with the variable term 2y in the other equation, and eliminating variable terms is our goal.
Let’s try it. We’ll multiply all parts of the first equation by 2. This turns this equation in to \(2x-2y=10\).
We manipulated the equation in this way because now we are set up for the term \(-2y\) and \(2y\) to cancel each other out when the two equations are added together. The variable will be eliminated, and this will leave us with a simpler equation to solve. We chose to add the two equations, and not subtract them, because the goal is elimination. If we add the equations, the terms cancel out. If we subtracted the equations, we would still be left with \(-4y\).
So let’s write this equation over here (\(2x-2y=10\)), and we’re going to add the equations together. When the \(2y\) and the \(-2y\) cancel out, we are left with \(3x+2x=5x=5+10=15\). Now, what we want to do is divide both sides by 5 and we get \(x=3\).
Now that we know that \(x=3\), we are halfway done. In order to find \(y\), we simply plug in our value of \(x\) into one of our equations, and solve for \(y\).
So let’s plug 3 into the equation \(x-y=5\), subtract 3 from both sides, gives us \(-y=2\) and divide by negative 1.
y equals negative 2
Now we have \(3-y=5\).
Let’s use inverse operations to solve for \(y\).
Subtract 3 from both sides, and then divide both sides by -1. We can see that \(y=-2 \).
This means that the solution to the system is \((3,-2)\).
In this example, we chose to add the two equations, in order for the variable terms \(2y\) and \(-2y\) to cancel out. However, there are times when you would need to subtract the two equations instead. You would choose to subtract the two equations in a situation where you had two variable terms that were the same, such as \(3y\) and \(3y\).
Review
Okay, before we go, let’s quickly review what we learned:
Linear equations describe a straight line on a graph, and are usually seen in slope-intercept form, \(y=mx+b\). We can solve systems of linear equations by using one of three methods. When using the graphing method, you first manipulate both equations so that they are in slope-intercept form, then graph both equations and identify the ordered pair where the lines intersect. The substitution method works by taking one of the equations, solving for one of the variables, and then plugging the solved variable into the other equation. When using the elimination method, you either add or subtract the equations to eliminate any one variable from the equations.
That’s all for this review! Thanks for watching, and happy studying!
Linear Equation Practice Questions
Solve the system of equations by graphing.
\(\begin{cases}y=x+1\\y=-2x-8\end{cases}\)
The correct answer is (-3, -2).
Step 1: Make sure both equations are in slope-intercept form. In this case, both equations are already in this form.
Step 2: Graph each line.
Step 3: Locate the point where the two lines intersect. In this case, the two lines intersect at the point (-3, -2).
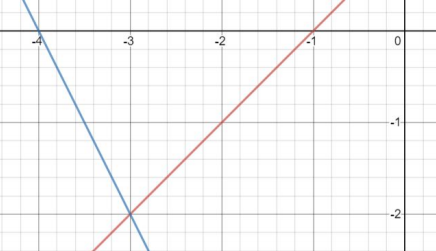
Solve the system of equations by graphing.
\(\begin{cases}x+y=7\\-2x+y=1\end{cases}\)
The correct answer is (2, 5).
Step 1: Make sure both equations are in slope-intercept form. To do this, start by using inverse operations to isolate the variable y in both equations. For the equation \(x+y=7\), subtract x from both sides. For the equation \(-2x+y=1\), add 2x to both sides. This leaves both equations in slope-intercept form.
\(\begin{cases}y=-x+7\\y=2x+1\end{cases}\)
Step 2: Graph each line.
Step 3: Locate the point where the two lines intersect. In this case, the two lines intersect at the point (2, 5).
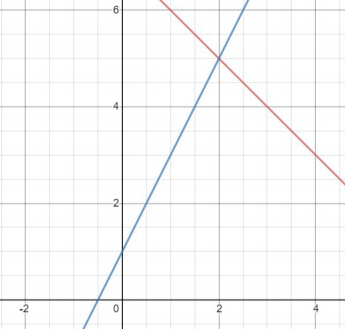
Solve the system of equations by graphing.
\(\begin{cases}2x+3y=1\\3x-y=7\end{cases}\)
The correct answer is (2, -1).
Step 1: Make sure both equations are in slope-intercept form. To do this, start by using inverse operations to isolate the variable y in both equations. For the equation \(2x+3y=1\), subtract 2x from both sides and then divide both sides by 3. For the equation \(3x-y=7\), subtract 3x from both sides, and then divide both sides by -1. This leaves both equations in slope-intercept form.
\(\begin{cases}y=\frac{-2}{3}x+\frac{1}{3}\\y=3x-7\end{cases}\)
Step 2: Graph each line.
Step 3: Locate the point where the two lines intersect. In this case, the two lines intersect at the point (2,-1).
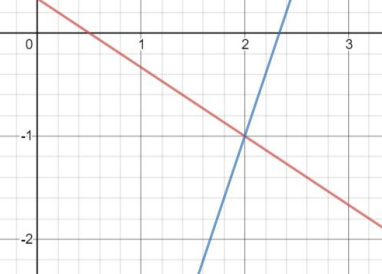
Solve the system of equations by substitution.
\(\begin{cases}2x+y=11\\7x-4y=-14\end{cases}\)
The correct answer is (2, 7).
Step 1: Solve one of the equations for y. In this case, solve the first equation. \(2x+y=11\) becomes \(y=-2x+11\).
Step 2: Using this newly solved equation, plug in the value of y into the y of the other equation. This is the substitution process.
\(7x-4(-2x+11)=-14\)
Step 3: Solve for x using inverse operations and the distributive property. This simplifies to \(7x+8x-44=-14\). Now, combine like-terms and the result will be \(15x-44=-14\). From here, add 44 to both sides and then divide by 15. This leaves \(x=2\).
Step 4: Plug in the value of x into one of the original equations. The variable x is equal to 2, so plug 2 into the equation \(2x+y=11\). Now \(2(2)+y=11\) and y needs to be solved. Subtract 4 from both sides and notice that \(y=7\). \(x=2\) and \(y=7\), so the solution is the point (2, 7).
Solve the system of equations by elimination.
\(\begin{cases}x-4y=-18\\-x+3y=11\end{cases}\)
The correct answer is (10, 7).
Step 1: When using the elimination strategy, look for a way to cancel out an x-term or a y-term when adding or subtracting the two equations. Notice that the x-terms would cancel out (x and –x) if these two equations were added.
Step 2: Add the two equations so that the x-terms will be eliminated.
Step 3: Solve for x. \(y=7\), so plug 7 in for y in the equation \(-x+3y=11\). This becomes \(-x+3(7)=11\), which simplifies to \(-x+21=11\). Subtract 21 from both sides and then divide by -1 in order to isolate the variable x. This results in \(x=10\). This means the solution is (10, 7).
