
Hi, and welcome to this review of ideal gas vs real gas!
“Ideal gas” is probably a term you’ve heard many times before, as the ideal gas law is often one of the first concepts taught in high school chemistry. While we will consider the ideal gas law, we’re also going to focus on the assumptions made about the particles of an ideal gas and discuss how it models real gas behavior.
Let’s get started!
Development of the Gas Law
To begin, let’s put ourselves in the shoes of the scientists who developed the ideal gas law. This was in the 1830s, when chemists didn’t necessarily have a molecular understanding of what a gas even was—that it consists of many tiny particles in constant motion bombarding surfaces to create pressure.
At the time, they were running experiments on different gases and recording the relationship between pressure, volume, temperature, and amount (or the number of moles). In doing so, they discovered direct relationships between these variables. For example, the volume of a gas increases with increasing temperature and the pressure decreases as volume increases. Importantly, they noticed that, at standard pressure and temperature, these relationships held up regardless of the type of gas.
Gas Law Example
So, for example, let’s say we have two balloons. The first balloon contains 1 mole of helium and the second balloon contains 1 mole of methane.
If both balloons were cooled from 80ºC to 40ºC, the volume of both balloons would decrease the exact same amount.
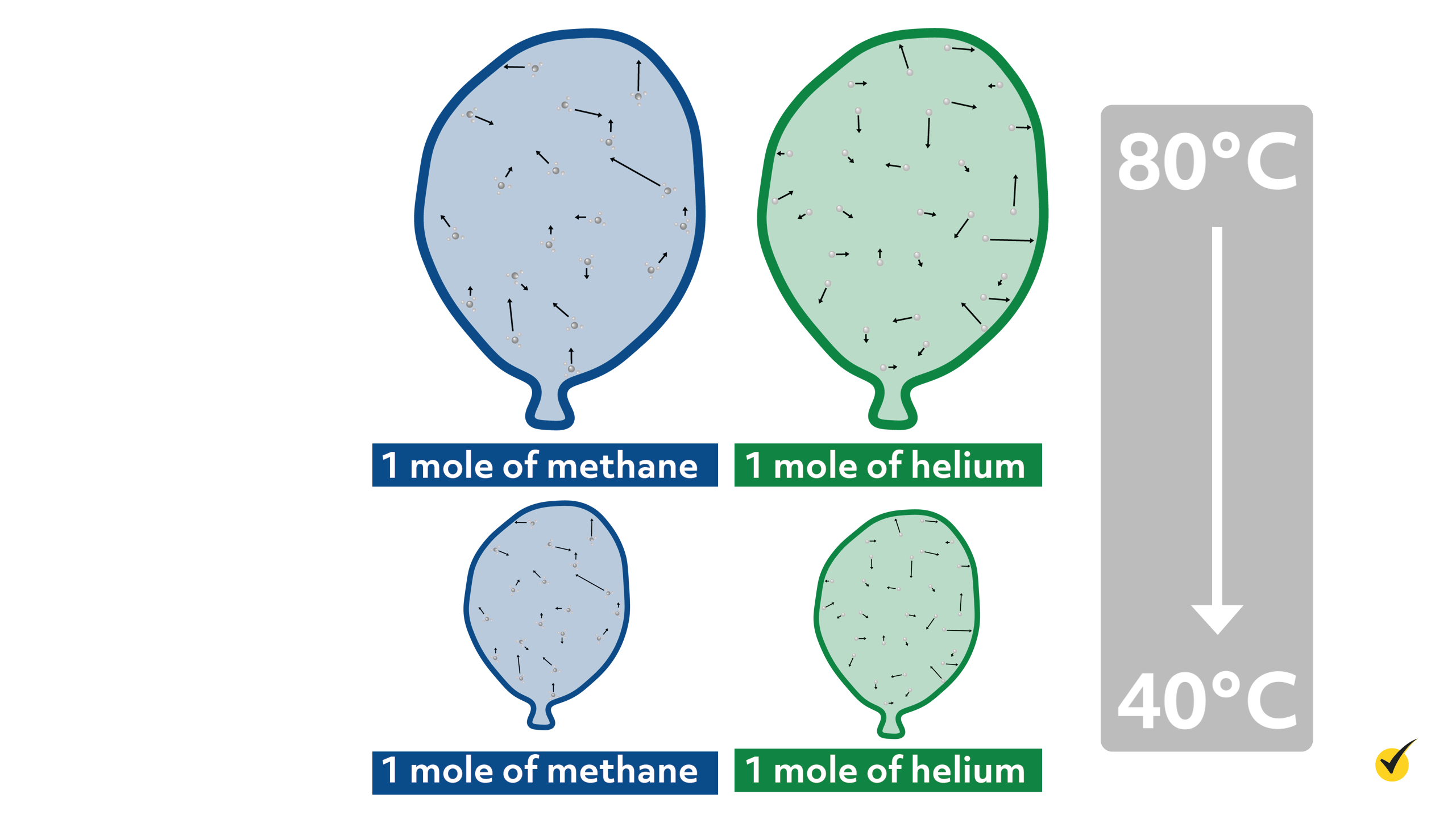
Thus, scientists concluded that the molecular properties of the gases didn’t matter much and that their behavior could be described by one simple relationship: \(PV=nRT\). Here, \(P\) is the pressure of the system, \(V\) is the volume, \(n\) is the number of moles, \(T\) is the temperature, and \(R\) is the molar gas constant.
Notice that there’s no variable to describe the specific gas, which means we can use this equation to calculate these properties for any gas!
So for both of those balloons, we could calculate their volume at either temperature with the ideal gas law; these balloons were blown up on earth, so have a pressure of approximately 1 atm.
\(V=\frac{nRT}{P}= \frac{(1 mol)(0.082058\frac{L\times atm}{mol \times K})(313 K)}{(1\text{ atm})}=25.7\text{ L}\)
And this led to the concept of the ideal gas—a gas, regardless of the conditions, that would always obey \(PV=nRT\). Remember, I mentioned that this held true only under certain conditions for real gases, and we’ll get to those in a minute.
Properties of Gas Particles
To always obey \(PV=nRT\), an ideal gas particle must have specific properties. First, they must have no volume and, second, they must have no interactions with each other. Essentially, they take up no space and there are no attractive intermolecular forces between the particles.
By this description, you probably recognize that an ideal gas particle is really just a theoretical tool rather than a real particle and that no real gases can truly be “ideal.” After all, real gases are made up of particles with volume and always exert some force on each other. But the ideal gas law is still pretty good at predicting the properties of most real gases when at certain conditions—specifically, low pressures and high temperatures. But why is that?
Behavior of Real and Ideal Gases
We can gain a deeper understanding of why real gases mimic an ideal gas at these conditions if we take a minute to consider what’s happening at the microscopic level.
First, at low pressures or large volumes, or more generally, at low densities of particles, the volume of the real gas particles is negligible in comparison to the volume of the container.
This means that we can assume the particles of the real gas to be volumeless, which makes them like an ideal gas. We can formally write this by saying that the volume of the container is much greater than the volume of the gas particles, so that the container volume minus the gas volume pretty much still equals the original container volume.
Secondly, as the temperature of a gas is increased, the average speed of the particles increases. This means that when the particles pass each other, they have very little time to interact, which, again, helps them mimic the behavior of an ideal gas. Thus, at relatively low pressures and high temperatures, real gases behave like ideal gases.
Macroscopic Observations
To see all this visually, we can consider a few graphs, which are commonly used to contrast the behavior of real and ideal gases.
In the first graph here, we have \(\frac{PV}{nRT}\) (denoted as \(Z\), the compressibility factor) plotted against the pressure of the system for helium, methane, and an ideal gas at 293 Kelvin (your typical room temperature).
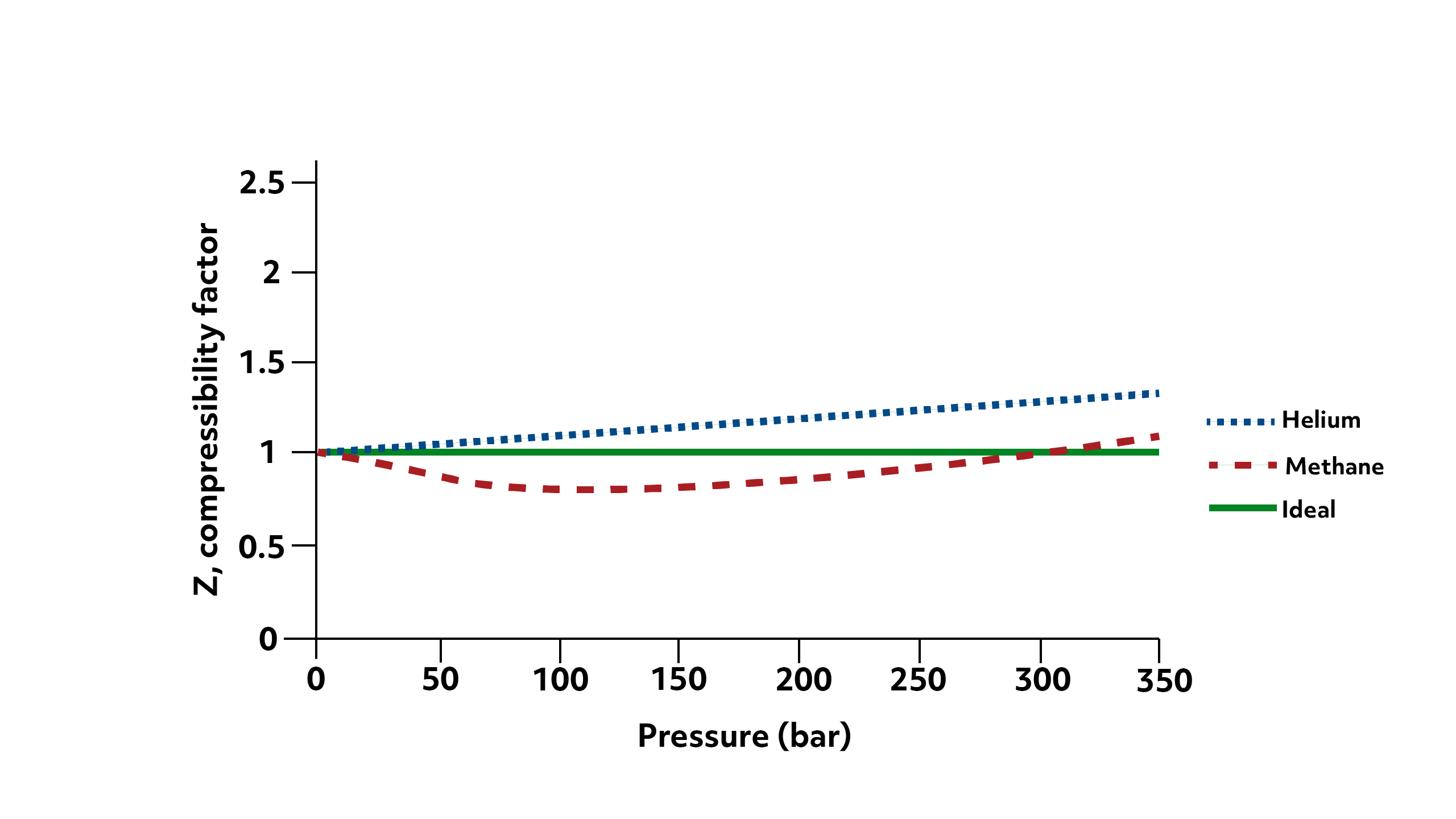
Notice that for the ideal gas, the solid line, the value is always 1 because \(PV=nRT\) by definition. For the two real gases, you can see that both have \(Z\)-values of about 1. They are essentially behaving ideally. And note that when we say “low pressures”, this includes atmospheric pressure (approximately 1 bar). So for most real gas problems happening on earth, we can comfortably approximate behavior with the ideal gas law.
However, as the pressure of the system increases, the assumption that our real gas particles are volumeless begins to fall apart.
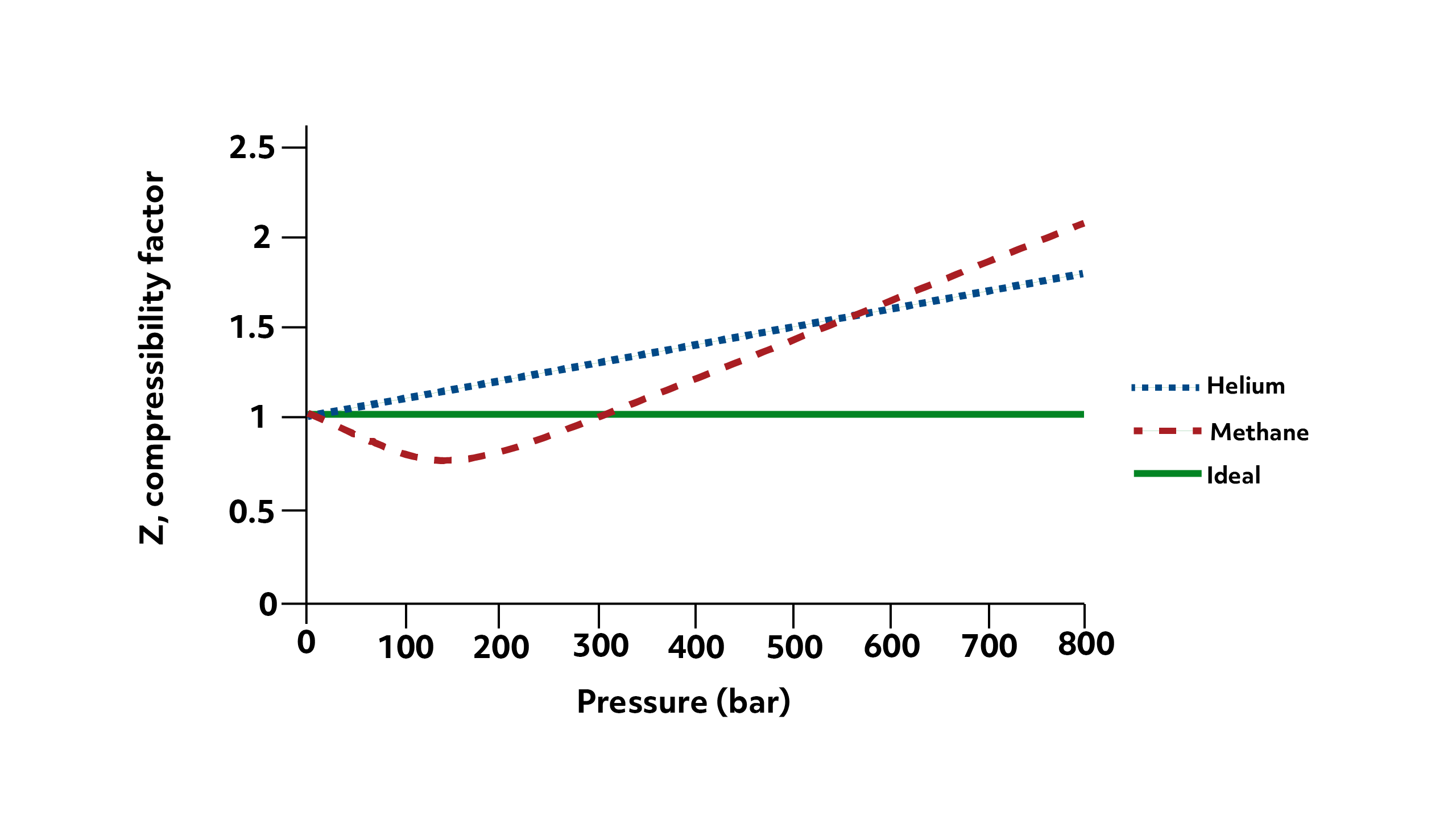
For real gases, as the pressure increases (by the volume decreasing) the particles themselves take up a more significant portion of the volume.
So, the volume of a real gas at high pressures is actually \(V_{\text{gas}}+V_{\text{container}}\), which, of course, is greater than \(V_{\text{container}}\) that’s used for ideal gas. This results in a Z value greater than 1, or positive deviations from the ideal gas law.
And as you can see from the graph, this gets more and more pronounced as the pressure continues to increase. This effect will be more significant for gases with larger particles- notice that at high pressures, methane’s Z value is greater than helium’s.
From the methane data, we also see that real gases have negative deviations from the ideal gas law at lower pressures, meaning their compressibility factor is less than 1.
This results from a collapse of the second assumption, that gas particles have no intermolecular interactions, which of course isn’t true. If we consider a real gas particle at the edge of the container, it feels a collective pull from the other particles away from the wall, thus decreasing the pressure it exerts on the vessel.
In total, this decreases the volume of a real gas in comparison to an ideal gas.
This effect depends both on the properties of the gas particles and the temperature of the system.
Large negative deviations will only occur for particles that have strong intermolecular interactions—notice that at 293 K helium has no negative deviation whereas methane does. This effect will also be particularly significant at lower temperatures. Remember that as temperature decreases the particles average speed decreases as well. This allows more time for the particles to strongly interact with each other.
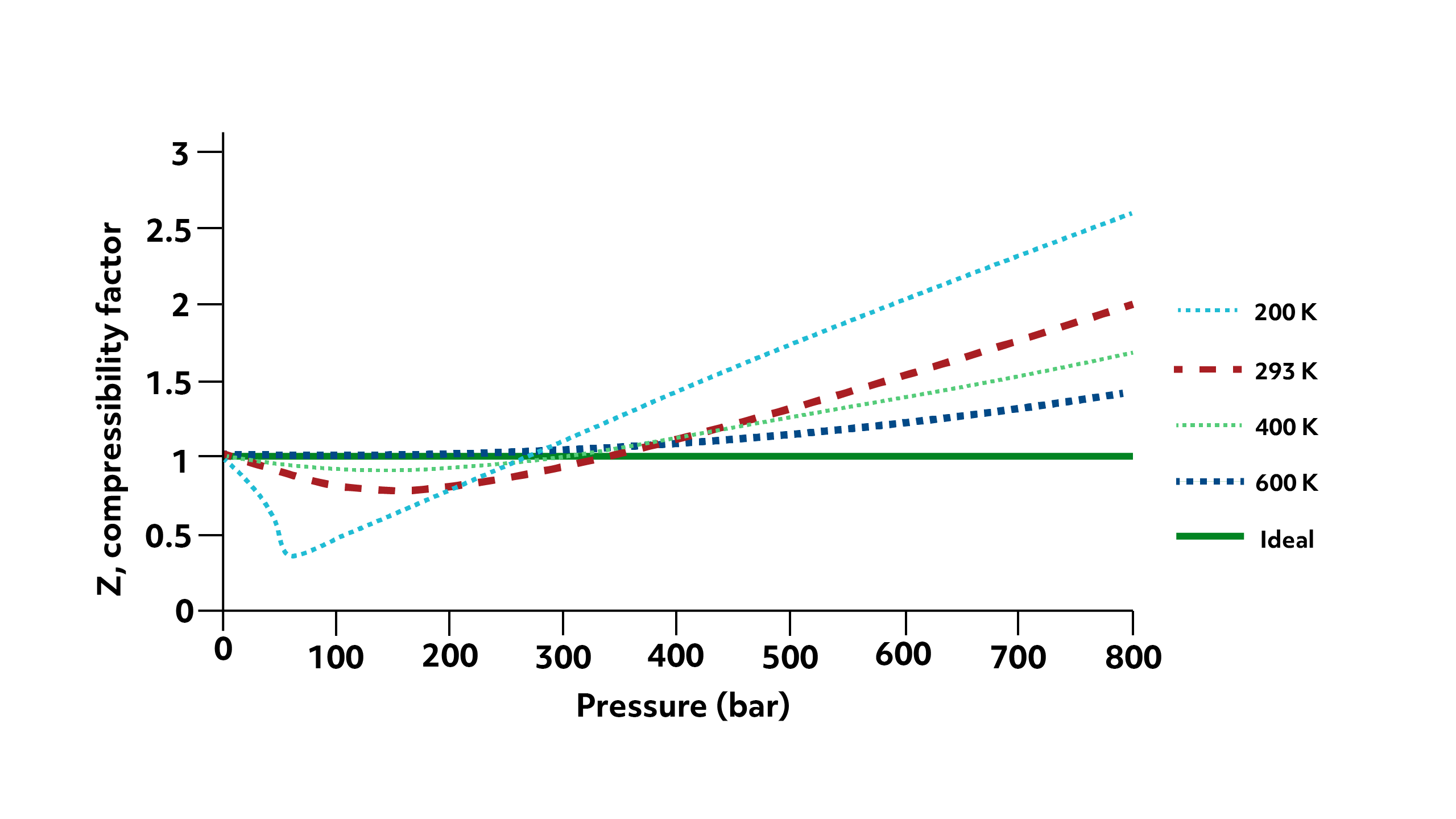
You can see this play out in the second graph. Here the Z of methane is plotted against pressure for 4 temperatures. At 200 K, the intermolecular interactions between methane particles significantly reduce the volume of the container, and we see a large negative deviation. This makes sense since we’re approaching methane’s condensation point, when it would simply convert to a liquid. However, as the temperature increases up to 600 K, methane behaves more or less ideally regardless of pressure.
Notice that as the pressure of the system increases, the positive deviations begin to outweigh the negative and at all temperatures, the deviations are all positive. The exact balance of when this transition will happen depends on the temperature of the system and the specific properties (like size and strength of interaction) of the gas particles themselves.
Review
Alright, let’s quickly review everything we’ve discussed.
An ideal gas is a theoretical gas composed of many randomly moving particles that are not subject to interparticle interactions. A real gas is simply the opposite; it occupies space and the molecules have interactions. This results in PV always equaling nRT.
While no real gas is truly an ideal gas, most follow these assumptions very well at low pressures and high temperatures. From a molecular perspective, this is true because this reduces the volume of the gas particles in comparison to the container and limits their ability to interact.
We also noted that the specific molecular properties affect their ideal behavior, with smaller, non-polar molecules behaving most ideally.
Practice Questions
Okay, before we go, let’s go over a couple of quick review questions:
1. Which molecule would you expect to deviate most from ideal behavior at high pressures?
- Methane
- Ethane
- Propane
- Butane
All four options are hydrocarbons, so they have similar intermolecular forces, but since butane is the largest, it’s most inaccurate to assume those particles are volumeless.
2. Under which conditions would you expect argon to behave most ideally?
- 150 K, 100 bar
- 400 K, 100 bar
- 150 K, 800 bar
- 400 K, 800 bar
These conditions, high temperature and low pressures, are when argon (or any particle) will behave the most like an ideal gas.
All right, that’s all for this review. Thanks for watching, and happy studying!