Hello and welcome to this video about the First Fundamental Theorem of Calculus! We will explore:
- What the theorem says
- How it works
- How it can be applied
But first, a little bit of background.
Recall that the area under a curve can be estimated by adding a number of rectangles or trapezoids. The more we add, the better our estimate. There are various ways to do this, but no matter how many we add, this method will always produce an estimate. The general calculations look like:
\(\sum_1^n \text{height}(f(x)) \times \text{width}(∆x)\) (rectangles) or \(\sum_1^n \frac{1}{2}(\text{base}(f(a+∆x))+\text{base}(f(a)))(\text{width}(∆x))\) (trapezoids)
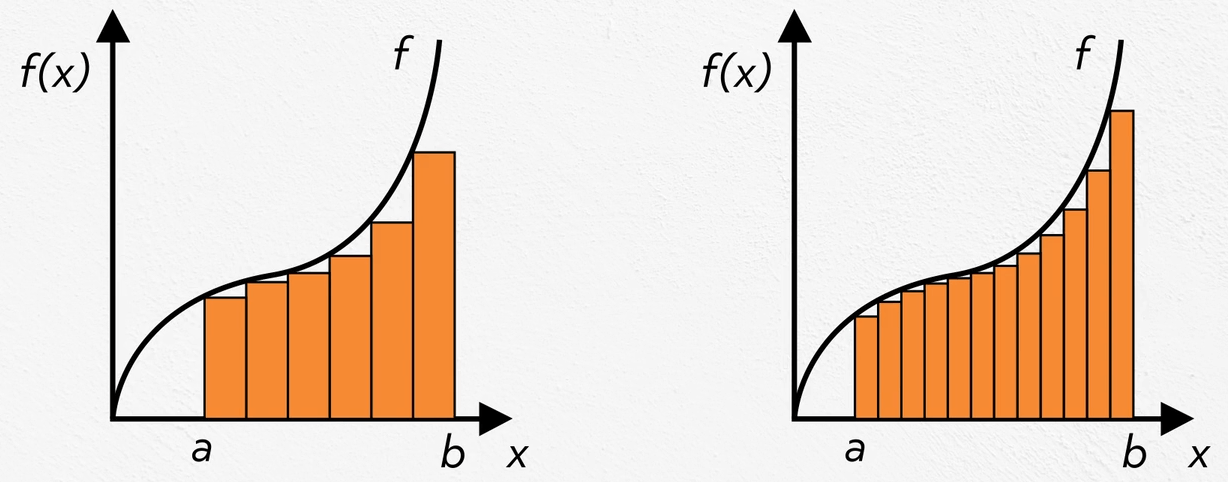
Also recall that antiderivatives are sort of “reversed” derivatives. In other words, the antiderivative of \(f(x)=x^2\) is \(F(x)=\frac{1}{3}x^3+C\) because the derivatives of all functions of the form \(\frac{1}{3}x^3+C\) are \(x^2\) by way of the Power Rule. Likewise, the antiderivative of \(f(x) = \cos{x}\) is \(F(x) =\sin{x} + C\), since the derivatives of all functions \(\sin{x} + C\) are \(\cos{x}\).
Usually, an indefinite integral is used to denote an antiderivative:
\(\int f(x)dx=F(x)+C\)Now for the big question, how would we find the exact area under a curve?
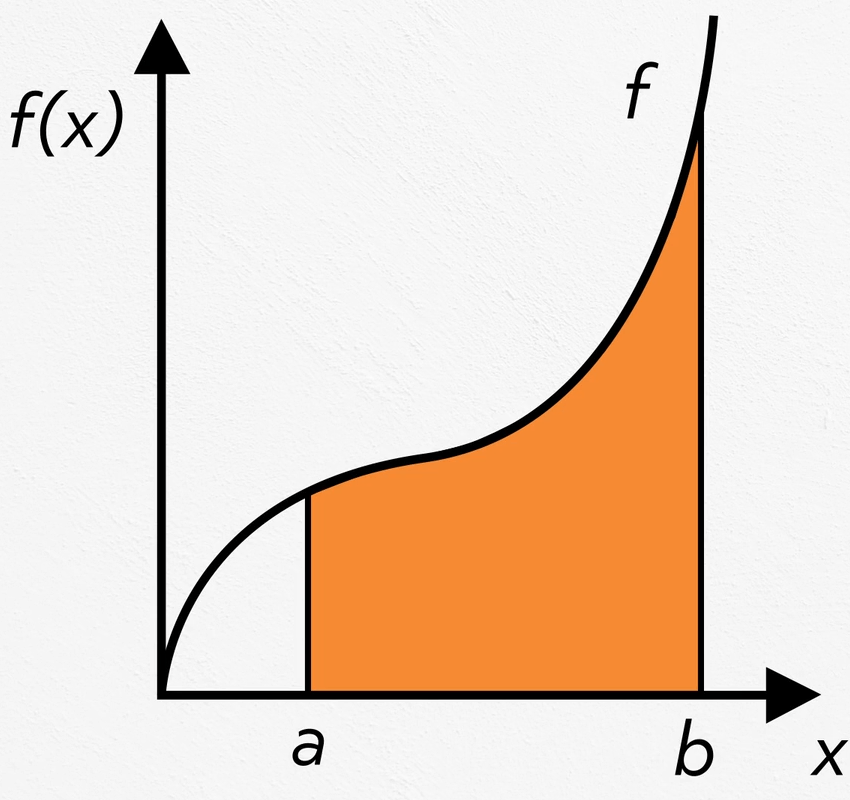
We would use the Fundamental Theorem of Calculus! There are two parts to this theorem (the second part has its own video) and the first part says:
If f(x) is continuous on [a,b] and \(\int f(x)dx=F(x)\) on [a,b], then
\(\int _a^b f(x)dx=F(b)-F(a)\)This represents the area over [a,b] from the x-axis to a function curve. This is called a definite integral because of the limits of integration. a is the lower limit (left boundary) and b is the upper limit (right boundary).
Here’s a quick demonstration. To find the area under the curve \(f(x)=x^2\) over the interval [-2,3]:
| \(\int_{-2}^3x^2 dx\) | Set up the definite integral. |
| \(\frac{1}{3}x^3|_{-2}^3\) | Find the antiderivative. The vertical bar indicates that the antiderivative has been found, but the final calculation has not yet been done. |
| \(F(b)-F(a)=F(3)-F(-2)\) =\(\frac{1}{3}(3)^3-\frac{1}{3}(-2)^3\) =\(9-(-\frac{8}{3})\) =\(\frac{35}{3}\) | The result is the area of the region. |
There are some properties to keep in mind.
- \(\int_a^a f(x) dx=F(a)-F(a)=0\)
The area of a region with 0 width is 0.
Switching the limits of integration makes the area negative. Traditionally, area is positive because it is thought of in terms of squares, both the shape and squaring numbers, which cannot be negative. In this case, since it changes the order of subtraction, the result changes signs. For example:
\(\int_3^{-2}x^2 dx=\frac{1}{3}x^3|_3^{-2}=F(-2)-F(3)=-\frac{8}{3}-9=-\frac{35}{3}\)A similar result happens when the function is below the x-axis. Making the function negative, we have:
\(\int_{-2}^3-x^2 dx=-\frac{1}{3}x^3|_{-2}^3=F(3)-F(-2)=-9-\frac{8}{3}=-\frac{35}{3}\)
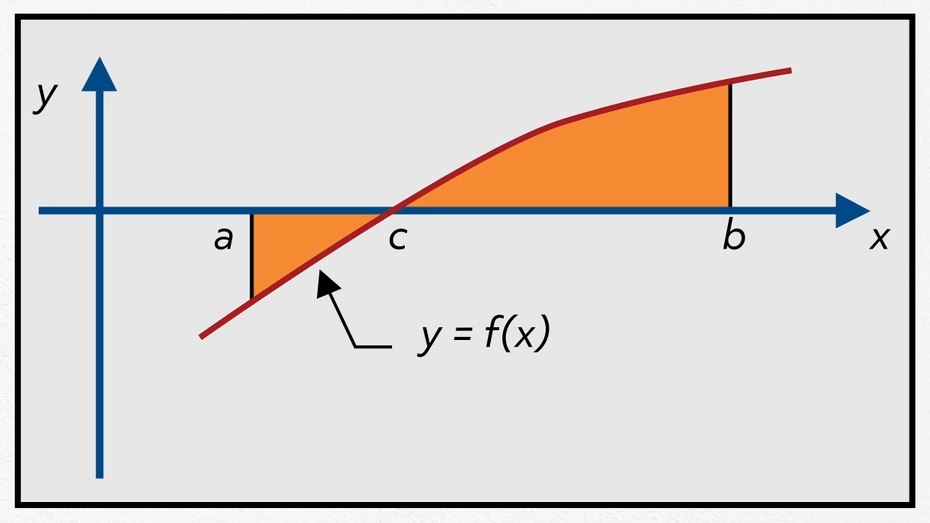
From this diagram, we can make several observations:
| \(\int_a^cf(x)\)<\(0\) | The area is being calculated from left to right and the region is below the x-axis. |
| \(\int_c^a f(x) dx\)>\(0\) | The area is being calculated from right to left and the region is below the x-axis. This is the equivalent of a double negative in language. |
| \(\int_c^b f(x) dx\)>\(0\) | The area is being calculated from left to right and the region is above the x-axis. |
| \(\int_b^c f(x) dx\)<\(0\) | The area is being calculated from right to left and the region is above the x-axis. |
| \(\int_a^b f(x) dx\)>\(0\) | The area is being calculated from left to right and the region below the x-axis is smaller than the region above the x-axis. |
| \(\int_b^a f(x) dx\)<\(0\) | The area is being calculated from right to left and the region below the x-axis is smaller than the region above the x-axis. |
| \(\int_a^a f(x) dx=\int_b^bf(x) dx=\int_c^cf(x) dx=0\) | These regions have 0 width. |
What does the area under the curve represent, other than a theoretical geometrical area? It can represent all kinds of things!
Suppose a function d(t) represents the distance (in miles) from home traveled over time (in hours) on a trip. d(1) would tell us our miles from home after one hour and d(10) would tell us our miles from home after 10 hours. The derivative function, d’(t), would tell us the rate of change of our distance from home, so d’(1) would tell us how fast we are going (mph) at 1 hour and d’(10) would tell us how fast we are going at 10 hours. Thinking in the other direction, \(\int_1^{10}d'(t)dt\) gives the total distance traveled from 1 hour to 10 hours.
Something important to note is that there’s a kind of hierarchy with functions, derivatives, and integrals:
| f(a) | Amount at x=a |
| f’(a) | How fast the amount is changing at x=a, i.e. velocity |
| \(\int_a^bf'(x) dx\) | Total amount from a to b |
Let’s take a look at an example.
Suppose water is draining from a tank at the rate of W(t)=-400(3-t) gal/min. How many gallons drain from 1-2 minutes?
\(\int_1^2W(t)dt=\int_1^2(-1200+400t) dt=-1200t+200t^2|_1^2=-1600-1000=-600\)600 gallons drain from the tank between minute 1 and minute 2. Note that we don’t have enough information at this point to figure out how much water is still in the tank. To figure that out we would need to know the initial amount or how much drained in the first minute.
Here are a few practice exercises. Pause the video and give them a shot!
- \(\int_{-2}^4(6x^2-10x+2)dx\)
=\(2x^3-5x^2+2x|_{-2}^4\)
=\((2(4)^3-5(4)^2+2(4))-(2(-2)^3-5(-2)^2+2(-2)\)
=96
- Use the solution from #1 for the following:
- \(\int_4^4(6x^2-10x+2)dx= 0\) [the limits are the same]
- \(\int_4^{-2}(6x^2-10x+2)dx= -96\) [the limits have been flipped]
- \(\int_{-2}^4(-6x^2+10x-2)dx= -96\) [the function was reflected over the x-axis]
- \(\int_4^{-2}(-6x^2+10x-2)dx= 96\) [the limits were flipped and the function was reflected over the x-axis]
- A particle moves along a straight line and has velocity function \(P(t)=-3t^2+24t-14\). How many meters does it travel from t=0 to t=3 seconds?
\(\int_0^3P(t)dt=-t^3+12t^2-14t|_0^3=-3^3+12(3)^2-14(3)=39\) meters
I hope that this video gave you a fundamental understanding of the First Fundamental Theorem of Calculus! Thanks for watching, and happy studying!
First Fundamental Theorem of Calculus Practice Questions
Find the area beneath the curve \(f\left(x\right)=8x^3-6x\) over the interval \(\left[1,3\right]\).
134
136
184
196
To find this area, compute the antiderivative of \(f\left(x\right)\), and then evaluate at the bounds 3 and 1. This can all be written as:
\(\int_{1}^{3}(8x^3-6x)\text{⬚} dx\)
The antiderivative of the first term, \(8x^3\), can be found by increasing the power of \(x\) by one and dividing by this new value. Raising \(x\) to the fourth power and dividing by four gives us \(\frac{8}{4}x^4\), or \(2x^4\). The antiderivative of the second term, \(-6x\), can be found by raising x to the second power and then dividing by two. This gives us \(-\frac{6}{2}x^2\), or \(-3x^2\). Altogether, the antiderivative is:
\(F\left(x\right)=2x^4-3x^2\)
Now, evaluate from 1 to 3. This step is written using a vertical bar, with the lower bound written at the bottom, and the upper bound written at the top.
\(2x^4-3x^2|^3_1\)
The first fundamental theorem of calculus says that the area beneath a curve on some interval \(\left[a,b\right]\) can be found by evaluating the antiderivative at \(b\), then subtracting the value of the antiderivative evaluated at \(a\). In this case, \(a=1\) and \(b=3\). First, evaluate \(F\left(x\right)=2x^4-3x^2\) at \(x=3\).
\(F\left(3\right)=2\left(3\right)^4-3\left(3\right)^2\)
\(F(3)=2\left(81\right)-3\left(9\right)\)
\(F(3)=162-27\)
\(F(3)=135\)
Then, evaluate at the lower bound, 1.
\(F\left(1\right)=2\left(1\right)^4-3\left(1\right)^2\)
\(F(1)=2\left(1\right)-3\left(1\right)\)
\(F(1)=2-3\)
\(F(1)=-1\)
Now, subtract \(F\left(3\right)-F\left(1\right)\) to get \(135-\left(-1\right)=135+1=136\).
Determine the value of \(\int_{0}^{2}-3x^2\text{⬚} dx\).
-12
-8
8
12
To evaluate this definite integral, first compute the antiderivative of \(-3x^2\). This can be done by raising the power of \(x\) by one and then dividing by the value of the new power.
\(f\left(x\right)=-3x^2\)
\(F\left(x\right)=-\frac{3}{3}x^3=-x^3\)
Now, because the bounds of the integral are from 0 to 2, evaluate at 0 and at 2 to find F\left(2\right)-F\left(0\right).
\(F\left(2\right)=-\left(2\right)^3=-8\)
\(F\left(0\right)=-\left(0\right)^3=0\)
\(F\left(2\right)-F\left(0\right)=-8-0=-8\)
This means that the area under the curve \(f\left(x\right)=-3x^2\) on the interval from 0 to 2 is equal to –8. The negative area value, in this case, is due to \(f\left(x\right)\) being a negative function, and the area appearing below the \(x\)-axis.
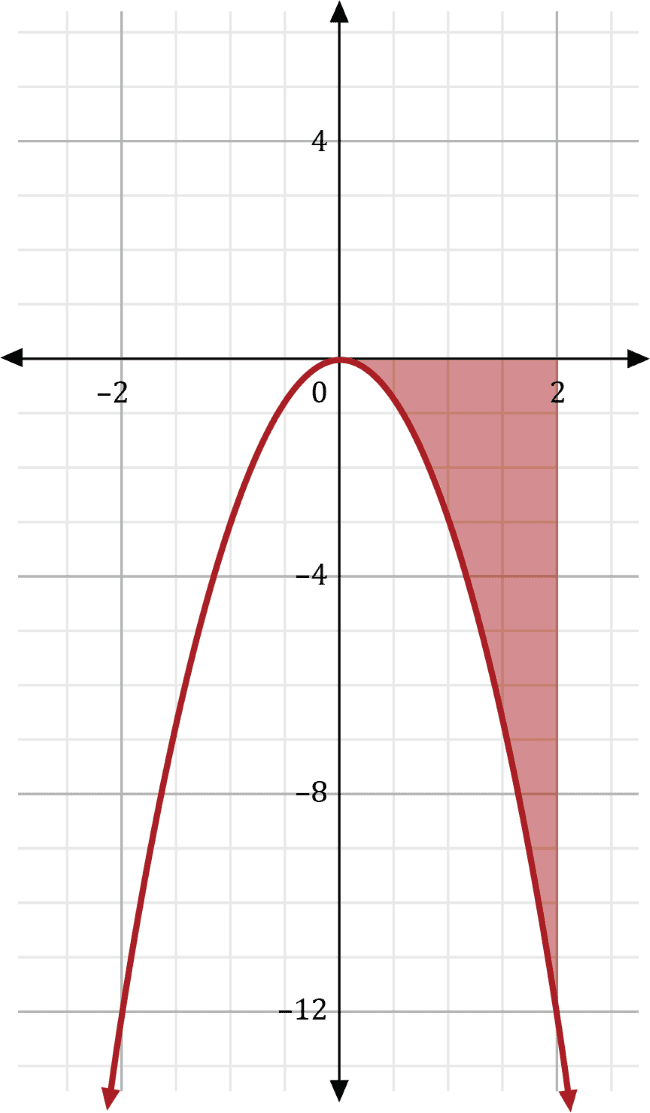
Find the area beneath the curve \(f\left(x\right)=sin\left(x^2\right)\) over the interval \(\left[100,100\right]\).
0
100
10,000
12,887
While this problem may look a bit tricky, notice the interval over which the integration occurs. Because the starting point and ending point of the interval are both 100, the interval has a width of zero. And a width of zero implies that the area will also be zero. This is confirmed by the first fundamental theorem of calculus over the interval \(\left[a,a\right]\) because
\(F\left(a\right)-F\left(a\right)=0\)
no matter what \(f\left(x\right)\) and \(F\left(x\right)\) are. The area beneath \(f\left(x\right)=sin\left(x^2\right)\) over the interval \(\left[100,100\right]\) is 0.
Susanna is studying the motion of a particle in a physics lab and determined that its velocity in micrometers per second at second \(t\) is equal to \(v\left(t\right)=sin\left(t\right)+5\). How far, in micrometers, does the particle travel from second 0 to second \(2\pi\)?
The definite integral of a velocity function gives us displacement. This problem requires finding the particle’s distance function \(V\left(t\right)\) and applying the first fundamental theorem of calculus to determine its distance traveled from \(t=0\) to \(t=2\pi\).
The distance function \(V\left(t\right)\) can be found by taking the antiderivative of \(v\left(t\right)\). First, \(sin\left(t\right)\) becomes \(-cos\left(t\right)\). Then 5 becomes \(5t\).
\(V\left(t\right)=-cos\left(t\right)+5t\)
Now, find \(V(2\pi)\), and then subtract the value for \(V\left(0\right)\).
\(V\left(2\pi\right)=-cos\left(2\pi\right)+5\left(2\pi\right)=-1+10\pi\)
\(V\left(0\right)=-cos\left(0\right)+5\left(0\right)=-1\)
\(V\left(2\pi\right)-V\left(0\right)=-1+10\pi-\left(-1\right)=10\pi\)
So, in \(2\pi\) seconds, the particle travels \(10\pi\) (or around 31) micrometers.
Sebastian is training for a 100-meter dash and tracked his speed throughout a 30-second sprint. He found that his speed, in meters per second, at second x could be determined using the function \(f\left(x\right)=-\frac{1}{100}x^2+\frac{2}{5}x+7\). How many meters did Sebastian travel from second \(x=15\) to second \(x=30\)?
161.25 meters
168.75 meters
170.5 meters
174.25 meters
To determine Sebastian’s distance traveled over a particular interval of time, first determine the distance function from the given speed function. This can be done by taking the antiderivative of his speed function \(f\left(x\right)\). For the first term, \(-\frac{1}{100}x^2\), increase the power of \(x\) by one and then divide by the value of the new power, 3. The first term becomes \(-\frac{1}{300}x^3\). For the second term, \(\frac{2}{5}x\), increase the power of \(x\) by one and then divide by the value of the new power, 2. The second becomes \(\frac{2}{5\cdot2}x^2\), or \(\frac{1}{5}x^2\). For the third term, 7, increase the power of \(x\) by one and then divide by the value of the new power, 1. The third term becomes \(7x\). Altogether, Sebastian’s distance function is \(F\left(x\right)=-\frac{1}{300}x^3+\frac{1}{5}x^2+7x\).
Now, evaluate his distance at \(x=30\) seconds, then subtract his distance at \(x=15\) seconds.
\(F\left(30\right)=-\frac{1}{300}\left(30\right)^3+\frac{1}{5}\left(30\right)^2+7(30)=\ 300\)
\(F\left(15\right)=-\frac{1}{300}\left(15\right)^3+\frac{1}{5}\left(15\right)^2+7(15)=138.75\)
\(F\left(30\right)-F\left(15\right)=300-138.75=\ 161.25\)
