
Hi, and welcome to this video on enthalpy!
There are a couple ways to approach this topic; often, textbooks begin with its derivation from internal energy. We will get to that briefly along with how to measure enthalpy, but first, we want to give enthalpy a more tangible definition before diving into the details.
Enthalpy in Chemical Reactions
To start, imagine any chemical reaction. What properties would you want to know about that reaction? Well, of course, you’d want to know the chemical components: the reactants, intermediates, and products. You’d also want to know the kinetics of the reaction; how fast is this reaction going to proceed?
And, lastly, you’d want to know about the thermodynamics. The thermodynamics would tell us about the equilibrium of the reaction, such as how much of the reactants will become products. It would also tell us whether the reaction would release or absorb heat (that is, whether it’s exothermic or endothermic). This is a really noticeable and easily measured feature of a reaction; you can often feel the temperature change of the reaction vessel with your hand! That release or absorbance of heat is the change of enthalpy for a reaction (with a few assumptions that we’ll get to in a minute).
Defining Enthalpy
Now that we have a physical idea of what enthalpy is, let’s turn to the more formal definition.
To begin with, there are lots of properties that can describe a system. So, how do we go about deciding which to measure? Well, our hands are often tied on this point because many properties are simply too difficult to measure. So even if they’re potentially very useful, if we can’t measure them quickly and reliably, they aren’t of much use. For example, the internal energy, denoted as U, is the total potential and kinetic energy of a system.
That’s an incredibly hard number to actually calculate. We’d have to infinitely separate out all the zillions of molecules and their subatomic particles and account for their kinetic energy. It’s basically impossible. So, rather than trying to measure the absolute internal energy of a system, we measure the change of the internal energy denoted by the capital delta, for instance, “the change in internal energy is equal to heat plus work”.
Internal Energy, Heat, and Work
Here, it’s important to remember that the first law of thermodynamics, energy cannot be created or destroyed, is always conserved. So heat and work, which could be mechanical work, electrical work, radiant work, basically any non-thermal energy, are the only two ways in which energy is transferred in or out of the system.
And we should remind ourselves of a second point here. While the energy in the universe is conserved, in most of our problems, we’ll split the universe into the system and its surroundings. Oftentimes in chemistry, we’ll define our reaction vessel as the system and the lab we’re in as the surroundings (since we don’t really need to consider the entire universe).
So, by measuring the released or absorbed heat and work done on or by a system over the course of a reaction, we can track the change in internal energy. Of those two quantities, we’re often more interested in the heat absorbed or released by a chemical reaction. However, heat and work are path functions, meaning they depend on the path the system takes to go from the initial to final state. This means that there are infinite combinations of heat and work that could account for a change in internal energy.
Other properties, like internal energy, pressure, and volume, on the other hand, are state functions, which means they only depend on the initial and final states, not on the pathway, of which there could be many. So, what we’d actually like is a state function that measures the heat released or absorbed by a system (spoiler- it’s enthalpy). But how do we get there?
Deriving Enthalpy from Internal Energy
First, we’ll begin with the change in internal energy and start by assuming that the only type of work done by our system is pressure-volume work, which means we’re ignoring all other types of work the system could be doing (like electrical, radiant, etc). So, we rewrite the change in internal energy as equal to heat minus pressure times the change in volume.
Very briefly, here’s how to think about PV work. Imagine a piston at the initial volume with a weightless and frictionless lid. A reaction occurs that increases the volume to the final volume, maintaining the internal pressure of the container. This work is considered negative because the system is doing work on the surroundings, so energy is transferred out of the system. This work is defined as the external pressure times the change in volume, which makes some intuitive sense because it’s how much the system pushed on the atmosphere.
Alright, let’s return to our definition of delta \(U\). Rearrange this equation to solve for heat, \(q\).
And now note that \(q\) is defined by the internal energy, pressure, and volume, which are all state functions. That means q can be expressed as a state function, which we will actually name enthalpy. This is represented by capital H and gets a delta here as well, because we’re measuring the change in enthalpy!
Importantly, notice that throughout this derivation we’ve been assuming constant pressure- if it changed, there would be a capital delta in front of \(P\) as well. This was especially noticeable when we defined work. The volume of the system changed to maintain the internal pressure.
This assumption that pressure isn’t changing is fundamental to the definition of enthalpy, which is formally written as the amount of heat absorbed or released by a system at constant pressure. This is denoted in the equation with the subscript \(P\) on heat.
This assumption turns out to be fine for most chemical reactions, as we often carry out reactions in open vessels at atmospheric pressure, which doesn’t change over the course of the reaction.
Just like internal energy, we could also define the absolute enthalpy of a system as:
But measuring the total enthalpy of a system would be really hard and isn’t super useful anyway. To illustrate this point with an everyday example, consider a mountain hike. While maybe you’re interested in the absolute altitude of your starting and ending point, the more important metric for you at that moment is the change in altitude.
It’s the same for enthalpy and internal energy- we’re most interested in their change during a chemical reaction rather than the absolute value.
Enthalpy Changes and Reaction Types
So, for a chemical reaction, instead of a mountain, we’ll define our stationary points as the reactants and products. The \(x\)-axis here is the reaction coordinate (which is essentially the progress of the reaction) and the y-axis is energy. Remember, heat is the transfer of thermal energy, so it should make some sense that enthalpy is measured in units of energy.
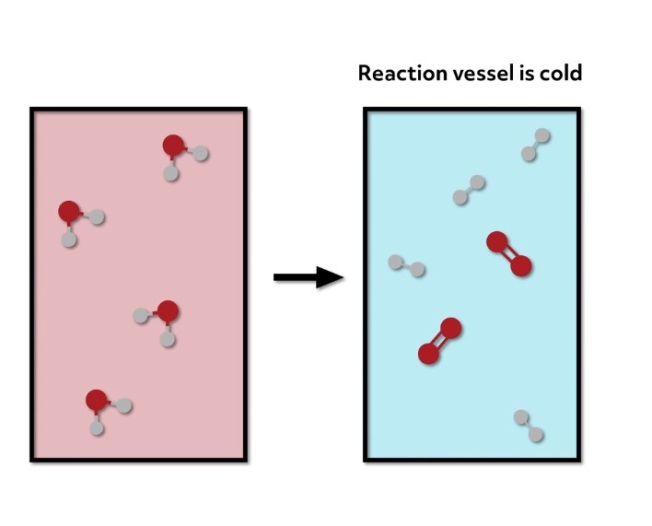
If the enthalpy of the system increases from the reactants to products, the change in enthalpy is positive and the reaction is endothermic.
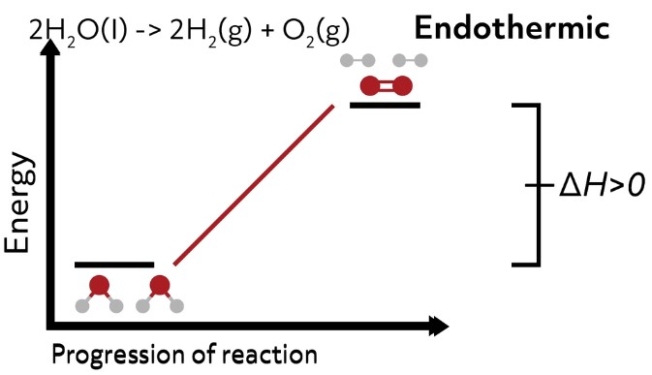
when \(H_{prod}\gt H_{react}\)
\(∆_{r}H\gt 0\)
The bonds of the reactants are more stable than the bonds of the products, so the system requires energy to form those new higher energy bonds in the products. In this case, the reaction vessel would feel cold to the touch.
Conversely, if the enthalpy of the system decreases from the reactants to products, the change in enthalpy is negative, and the reaction is exothermic.
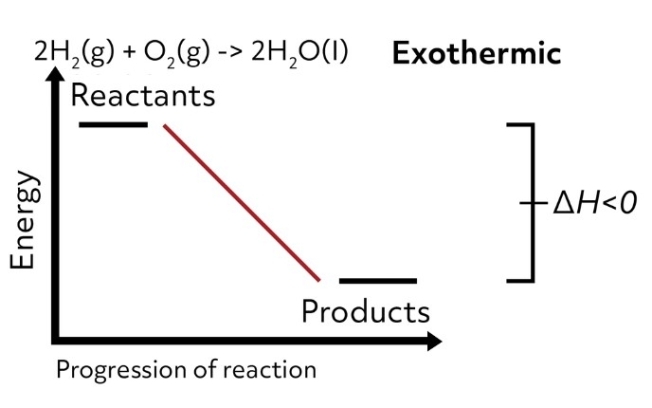
The bonds of the reactants are less stable than the bonds of the products, so the system releases that excess energy as heat when the products are formed. In this case, the reaction vessel would feel hot to the touch.
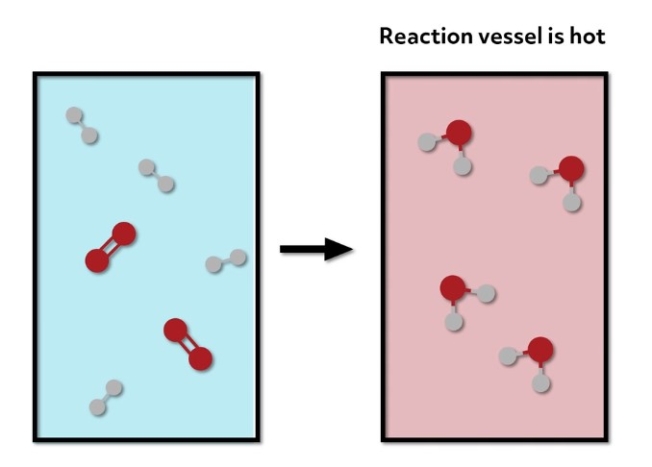
And this is a really important point. Many, many times students get confused about “breaking bonds to release energy.” That sentence is a very common misconception. Breaking bonds costs energy. Energy is only released when you form bonds that are more stable than the ones you have broken. So the change in enthalpy for a reaction, whether it’s exo- or endothermic, is telling us directly about the relative energy of the reactant and product bonds.
To experimentally measure the change in enthalpy for a reaction, we could run a calorimetry experiment. We could measure the change in temperature during the course of the reaction and then using the specific heat capacity and mass of the substance, could convert that temperature change to the change in enthalpy.
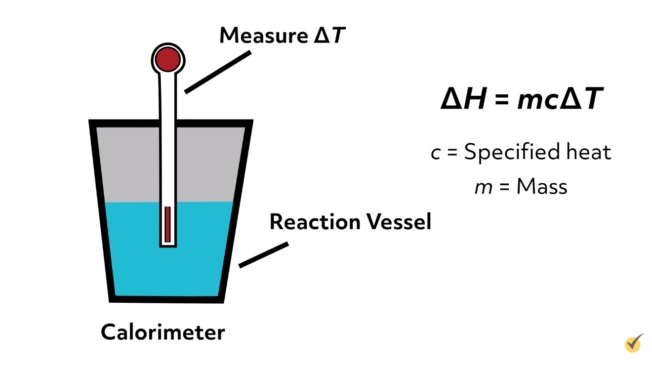
Review
Okay, we’ve covered a lot of information in this video, so let’s go back over everything with a quick review.
We started by deriving the standard definition of enthalpy from the change in internal energy, which is equal to the sum of heat and work. To do so, we assumed that the only work the system does is mechanical pressure-volume work and that pressure is constant during the course of the reaction, two assumptions that are usually safe to make. We then defined endo- and exothermic reactions in terms of their enthalpy change.
Throughout, we discussed how for these state functions, we’re rarely interested in absolute values and usually calculate the change in enthalpy and internal energy. And we finished with a discussion of how enthalpy is calculated experimentally by touching on the concept of calorimetry.
Alright, that’s it for today’s video! Thanks for watching, and happy studying!