Derivatives of Exponential and Log Functions

Today we begin with a brain teaser: is it possible to construct a function whose height at a given point \(x\) is equal to its slope at that same point \(x\), over the entire domain? In other words, is it possible to construct a function whose derivative is itself?
Derivatives of Exponential and Logarithmic Functions
Today we begin with a brain teaser: is it possible to construct a function whose height at a given point \(x\) is equal to its slope at that same point \(x\), over the entire domain? In other words, is it possible to construct a function whose derivative is itself?
\(\frac{d}{dx}f(x)=f(x)\)
In this lesson, we are going to discuss the possibility of such a function, but we are going to start by talking about logarithmic and exponential functions, and how to take their derivatives.
First, let’s quickly review how log functions are used. Logarithms are written in the format \(\log_{a}{b}=c\), where \(a\) is the base, \(b\) is the argument, and \(c\) is the exponent. Writing \(\log_{a}{b}=c\) is equivalent to writing \(a^{c}=b\). For example, what does \(\log_{3}{9}\) equal? We can answer this by asking, “3 raised to what power equals 9?” Clearly, \(3^{2}=9\), so \(\log_{3}{9}=2\).
The most common logarithmic function we use in calculus is the natural log, written “ln”. “ln” is equivalent to log base \(e\).
\(\ln{x}=\log_{e}{x}\)
As a quick example, what is \(\ln{1}\) equal to? Remember that \(e\) is the base of all natural logs, and ask yourself, “\(e\) (the base) raised to what power equals 1?” The answer is 0.
\(\ln{1} = 0\text{ because } e^{0}=1\)
Now that we have refreshed our memories on how to use the natural log, we need to talk about its derivative. Fortunately, \(\ln\)’s derivative is surprisingly simple: the derivative of \(\ln{x}\) is equal to \(\frac{1}{x}\).
\(\frac{d}{dx}\ln{x}=\frac{1}{x}\)
Let’s use this to work out the derivative of the function \(f(x)=\ln{x}+3x\). This function is a polynomial, so we look at each term individually. As we just said, the derivative of \(\ln{x}\) is \(\frac{1}{x}\), and we know that the derivative of \(3x\) is simply 3. Therefore, \(f'(x)=\frac{1}{x}+3\).
Now, what if we wanted to find the derivative of the function \(g(x)=\ln{(3x+4)}\)? It is tempting to say that the derivative should be \(\frac{1}{3x+4}\), but because \(3x+4\) is a function within our function \(g(x)\), we must instead use the chain rule. Applied to the natural log, the chain rule tells us that the derivative of \(\ln{u}\), where \(u\) is the internal function, is equal to \(\frac{1}{u}\) multiplied by the derivative of \(u\).
\(\frac{d}{dx}\ln{u}=\frac{1}{u}\cdot \frac{du}{dx}\)
Let’s use this formula now to find \(g'(x)\). In this problem, \(u=3x+4\), so \(\frac{du}{dx}=3\).
\(g'(x)=\frac{1}{3x+4}\cdot 3\)
We can then simplify this to be:
\(\frac{3}{3x+4}\)
Let’s work one more example before moving on. Find the derivative of \(\ln{(4x^{2}+5x)}\). To solve this derivative, we just need u, its derivative, and the chain rule formula. In this problem, let u equal what is inside the natural log, so \(4x^{2}+5x\). We’ll then take the derivative of this to get \(\frac{du}{dx}\), which will be \(8x+5\).
\(u=4x^{2}+5x\), so \(\frac{du}{dx}=4\cdot 2x+5=8x+5\)
Plugging these into the formula, we have this:
\(\frac{d}{dx}\ln{(4x^{2}+5x)}=\)\(\frac{1}{4x^{2}+5x}\cdot (8x+5)\)\(=\frac{8x+5}{4x^{2}+5x}\)
So the derivative of \(\ln{(4x^{2}+5x)}\) is equal to \(\frac{8x+5}{4×2+5x}\).
Let’s now talk about the natural exponential function. As you may have guessed from its name, the natural exponential function involves \(e\), just like the natural log does. It is written \(e^{x}\), and its graph looks like this:
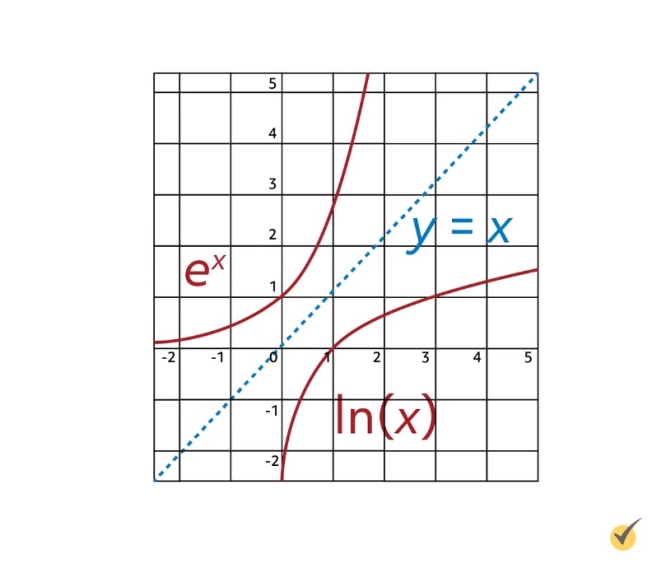
The relationship between \(e^{x}\) and the natural log of \(x\) can actually be shown graphically, because they are each other’s inverses, reflected across the line \(y=x\).
Remember the brain teaser from the beginning of this video? It turns out that the natural exponential function has several important properties, one of which is that it is the only function whose derivative is itself!
\(\frac{d}{dx}e^{x}=e^{x}\)
This is a fascinating fact that will help us greatly with derivatives of functions containing exponentials, but how can we be sure it is true? Let’s see if we can prove it now.
We can start by writing the function as \(y=e^{x}\).
\(y=e^{x}\)
Now, remember we said that the natural exponential function is the inverse of the natural log. We will use this fact, along with a special property of ln to modify our starting expression. First, let’s take the natural log of both sides, so that we have \(\ln{y}\) is equal to \(\ln{(e^{x})}\).
\(\ln{y}=\ln{(e^{x})}\)
Can \(\ln{(e^{x})}\) be simplified? Ask yourself, “\(e\), the base, raised to what power gives us \(e^{x}\)?” Obviously, \(e\) raised to \(x\) does! That means that the right side of the equation is equivalent to \(x\).
\(\ln{y}=x\)
The next step in this proof is a little bit sneaky, so follow along carefully. We are going to differentiate both sides with respect to \(x\). Since \(y\) is a function, we need to treat the left side with the chain rule. Using the formula from earlier, this gives us \(\frac{1}{y}\) multiplied by the derivative of \(y\) with respect to \(x\), \(\frac{dy}{dx}\). The derivative of \(x\), on the right side, gives us 1.
\(\frac{1}{y}\cdot \frac{dy}{dx}=1\)
To simplify this expression, multiply both sides by \(y\). This will eliminate the fraction on the left, and leave us with \(\frac{dy}{dx}=y\).
\(y\cdot \frac{1}{y}\cdot \frac{dy}{dx}=1\cdot y\)
\(\frac{dy}{dx}=y\)
We now have that the derivative of \(y\) with respect to \(x\) is \(y\)! That means that \(y=e^x\) does in fact have the special property of being its own derivative!
We can also observe this fact graphically. Look at the graph of \(y=e^{x}\) and see that at height \(y=1\), \(e^{x}\) has a slope of 1. Similarly, at height \(y=2\), \(e^{x}\) has a slope of 2, and at height \(y=4\), it of course has a slope of 4.
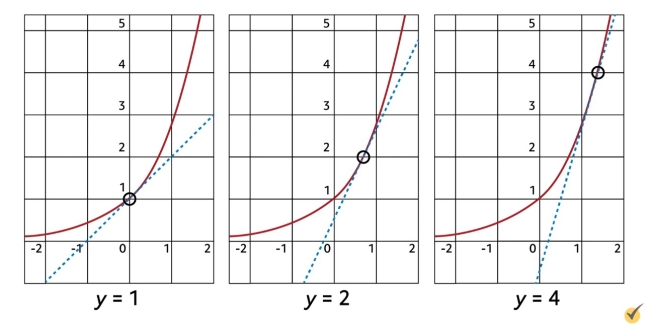
Since \(e^{x}\) is its own derivative, you can determine the derivative of \(f(x)=4e^{x}\). To solve, we’ll use the product rule. \(f’\) will equal 4 times the derivative of \(e^{x}\), plus \(e^{x}\) times the derivative of 4. It is unsurprising that this gives us \(f'(x)=4e^{x}\).
\((f\cdot g)’=f\cdot g’+g\cdot f’\)
\(\frac{d}{dx}4e^{x}=4\cdot e^{x}+e^{x}\cdot 0=4e^{x}\)
A lot of derivative problems involving the natural exponential function require the use of the chain rule, which by now you should be plenty familiar with. Whenever a function appears in the exponent above \(e\), use the formula:
\(\frac{d}{dx}e^{u}=e^{u}\cdot \frac{du}{dx}\)
For example, we can find the derivative of \(e^{\sin{(x)}}\) by using the chain rule. For this function, \(u=\sin{(x)}\), and the derivative of \(u\), \(\frac{du}{dx}\), is equal to \(\cos{(x)}\). Plugging these into the chain rule formula gives us:
\(\frac{d}{dx}e^{\sin{(x)}}=e^{\sin{(x)}}\cdot \cos{(x)}\)
The natural exponential function helps scientists model real-life phenomena like compound interest, population levels, and radioactive decay. Test your comprehension now with this practice problem:
Biologists studied the population of horses on a certain wildlife reserve and found that it could be modeled closely with the function \(h(x)=e^{\frac{1}{x}}+3 \ln{x}\), where \(x\) represents the number of years since the study began. What is the rate of change in this population?
Pause the video now to find the solution on your own.
I hope you gave it your best shot! The correct answer is \(h'(x)=-\frac{e^{\frac{1}{x}}}{x^{2}}+\frac{3}{x}\). Let’s work through the problem together now. We are given the function \(h(x)\) to model the population, and we are asked to find the rate of change in that population. This phrasing indicates that we need to take the derivative of \(h\).
The first term of \(h\) is \(e^{\frac{1}{x}}\), which we can differentiate using the chain rule. Set \(u=\frac{1}{x}\), and note that the derivative of \(u\) is then \(-\frac{1}{x^{2}}\). The chain rule formula tells us that:
\(\frac{d}{dx}e^{\frac{1}{x}}=e^{\frac{1}{x}}\cdot (-\frac{1}{x^{2}})=-\frac{e\frac{1}{x}}{x^{2}}\)
The second term, \(3 \ln{x}\), is easier to differentiate. Use the product rule to see that its derivative is simply \(\frac{3}{x}\).
\(\frac{d}{dx}3 \ln{x}=\ln{x}\cdot 0+3\cdot \frac{1}{x}\)\(=\frac{3}{x}\)
Put these two terms together to get \(h'(x)\), the rate of change in population.
\(h'(x)=-\frac{e^{\frac{1}{x}}}{x^{2}}+\frac{3}{x}\)
Now that we have gone over the natural log, the natural exponential function, and their derivatives, there are just a few more useful properties and applications for us to discuss.
First, we can combine the properties of \(\ln{x}\) and \(e^{x}\) to solve expressions with a variable in the exponent. For example, given the expression \(a^{x}\), where \(a\) is a positive real number and \(x\) is any real number, you can solve for \(x\) by using the formula \(a^{x}=e^{x\ln{a}}\).
For example, if we are given the equation \(2^{x}=128\), we can solve for \(x\) using this formula. This equation can instead be expressed as \(e^{x\ln{2}}=128\). From here, take the natural log of both sides to bring the exponent down:
\(\ln{(e^{x\ln{2}})}=\ln{(128)}\)
On the left side, the \(\ln\) and the \(e\) cancel each other out, leaving us with:
\(x\ln{(2)}=\ln{(128)}\)
Dividing both sides by \(\ln{2}\), \(x=\frac{\ln{(128)}}{\ln{(2)}}\). This solution can be simplified to \(x=7\) by using a calculator.
A second application is taking the derivative of such an expression. Use the formula
\(\frac{d}{dx}a^{x}=a^{x}\ln{a}\)
to do so. Following from the previous example, if we were to take the derivative of \(2^{x}\), this derivative formula tells us:
\(\frac{d}{dx}2^{x}=2^{x}\ln{2}\)
Of course, if we have a function with another function in the exponent, we can apply the chain rule to this derivative formula. That is:
\(\frac{d}{dx}a^{u}=a^{u}\ln{a}\frac{du}{dx}\)
Using this in an example, we can take the derivative of a function like \(2^{2x+1}\) by following the formula and applying the chain rule. Here, \(u=2x+1\), and \(\frac{du}{dx}=2\).
\(\frac{d}{dx}2^{2x+1}=2^{2x+1}\ln{(2)}\cdot 2\)\(=2^{2x+2}\ln {(2)}\)
Finally, if you need to take the derivative of a logarithmic function whose base is not \(e\), use the following formula:
\(\frac{d}{dx}(\log_{a}{x})=\frac{1}{x\ln{a}}\)
Or, if the argument of the logarithm is a function \(u\) (I’m sure you guessed it!), apply the chain rule to this formula to get:
\(\frac{d}{dx}(\log_{a}{|u|})=\frac{1}{u\ln{a}}\cdot \frac{du}{dx}\)
Note that because \(u\) appears in the denominator, this formula can only be used when \(u\neq 0\).
I hope that this lesson has helped you form a better understanding of the functions \(e^{x}\), \(\ln{x}\), and finding their derivatives using the chain rule.
Thanks for watching, and happy studying!
