What is a Mole Ratio?
Hi, and welcome to this video on the mole ratio, sometimes referred to as the molar ratio. It’s a fundamental concept in chemistry that’s used to convert back and forth between moles of each substance in a reaction. Among other things, it’s necessary for calculating theoretical yields and limiting reagents. This is most certainly a concept best learned through examples, so let’s jump right in.
Before we put these mole ratios to use, let’s consider a more relatable example to solidify this concept.
When you make mac n’ cheese, you always use the same ratio of ingredients. One box of pasta, 1 packet of cheese, 3 tablespoons of milk, and 2 tablespoons of butter.
1 box pasta + 1 packet of cheese + 3 tbsp milk + 2 tbsp butter = 1 mac n’cheese
Our “mole ratio”, so to speak, for milk and mac n’ cheese is 1 mac n’ cheese over 3 tablespoons of milk.
\(\frac{1\text{ mac n’cheese}}{3\text{ tbsp milk}}\)
So, for every 3 tablespoons of milk, we can make one recipe of mac n’ cheese.
We could do this for any combination of species in the reaction. For example, for every packet of cheese we have, we need 2 tablespoons of butter.
\(\frac{2\text{ tbs butter}}{1\text{ packet of cheese}}\)
And of course, if we want more mac n’ cheese we can double the recipe.
2 boxes pasta + 2 packets of cheese + 6 tbsp milk + 4 tbsp butter = 2 mac n’cheese
If we did that, the ratio between ingredients would stay the same.
So, in fact, anytime you follow a recipe, you’re basically employing the concept of mole ratios, so keep that in mind the next time you’re cooking!
Now let’s put these mole ratios to work by looking at the formation of ammonia from nitrogen and hydrogen.
N2 + H2 ⇌ NH3
First, as written, this is an unbalanced chemical equation. On the reactants side of the equation, we have 2 atoms of nitrogen and 2 atoms of hydrogen, while on the product side, we only have 1 atom of nitrogen but 3 atoms of hydrogen.
We can’t even discuss the concept of the mole ratio for a reaction if it is unbalanced. So let’s balance this first.
Remember, we can’t change the molecules, split bonds, or change the chemistry in any way. We’re stuck working with the molecules we’re given, so to balance a reaction we can only increase the number of each molecule by adjusting the stoichiometric coefficients.
To balance this reaction, we need 1 molecule of nitrogen gas, 3 molecules of hydrogen gas, and 2 molecules of ammonia. Now we have 2 nitrogen atoms and 6 hydrogen atoms on both sides of the equation.
N2 + 3H2 ⇌ 2NH3
Said another way, to make 2 molecules of ammonia, we need 1 molecule of nitrogen and 3 molecules of hydrogen. To have a balanced reaction with no leftover atoms, the chemistry demands this ratio of molecules.
We could, of course, multiply by a factor, say of 2, so that 2 molecules of nitrogen plus 6 molecules of hydrogen make 4 molecules of ammonia, which still works because we haven’t changed the underlying ratio between molecules. In other words, 1 divided by 3 equals 2 divided by 6.
We can extend this to the mole scale, as in, when we think about zillions of molecules reacting at once. Remember- a mole is an amount of something equivalent to 6.022 x 1023 units, which could be atoms, ions, electrons, or, like in this case, molecules. So when we say that 1 mole of nitrogen is needed to react with 3 moles of hydrogen to make 2 moles of ammonia, we’re saying that we need 6.022 x 1023 molecules of nitrogen to react with 18.066 x 1023 molecules of hydrogen to make 12.044 x 1023 molecules of ammonia. While those are much larger numbers than 1, 2, and 3, the ratio is maintained between the molecules.
Another way of phrasing this is that 1 mole of nitrogen is stoichiometrically equivalent to 3 moles of hydrogen when making ammonia. This means that 1 mole of nitrogen gas will make you the same amount of ammonia as 3 moles of hydrogen. So even though we have different amounts of each substance, when it comes to making ammonia, we can think of them as being equivalent.
We can actually write this out in an equation.
For the formation of ammonia, one mole of nitrogen gas is stoichiometrically equivalent to 3 moles of hydrogen gas.
1 mol N2 = 3 mol H2
We can then rearrange this to get the actual mole ratio 1 mole of nitrogen gas over 3 moles of hydrogen gas is equal to 1.
\(\frac{1\text{ mol }N_2}{3\text{ mol }H_2}=1\)
We now can use this to convert between moles of hydrogen to moles of nitrogen, which will be very useful when we need to calculate yields or limiting reagents.
\(\frac{3\text{ mol }H_2}{1\text{ mol }N_2}\)
Of course, we could flip the ratio if we needed to convert from moles of nitrogen to moles of hydrogen.
Similarly, we can write out the molar ratios for the other two combinations of reactants and products.
\(\frac{1\text{ mol }N_2}{2\text{ mol }NH_3}\)
As you can see here, for every 1 mole of nitrogen, we can make 2 moles of ammonia
\(\frac{3\text{ mol }H_2}{2\text{ mol }NH_3}\)
and for every 3 moles of hydrogen, we can make 2 moles of ammonia.
Now let’s think about how we actually use mole ratios in chemistry problems.
Let’s say we wanted to make 10 moles of ammonia- how many moles of nitrogen and hydrogen would we need? With our mole ratios, this is a simple problem. Let’s work out the hydrogen first. 10 moles of ammonia times 3 moles of hydrogen gas over 2 moles of ammonia equals 15 moles of hydrogen gas.
\(10\text{ mol }NH_3(\frac{3\text{ mol }H_2}{2\text{ mol }NH_3})=15\text{ mol }H_2\)
Okay, now let’s work out the nitrogen. 10 moles of ammonia times 1 mole of nitrogen gas over 2 moles of ammonia equals 5 moles of nitrogen gas.
\(10\text{ mol }NH_3(\frac{1\text{ mol }N_2}{2\text{ mol }NH_3})=5\text{ mol }N_2\)
So, to make 10 moles of ammonia, we need 15 moles of hydrogen and 5 moles of nitrogen.
Notice that when you write these calculations out, it’s very useful to specify the chemical species to which you are referring. So rather than just writing “4 moles”, write “4 moles NH3” to keep track of each.
Let’s move on to a slightly more complicated problem. Say we had 1 kilogram of nitrogen gas and wanted to know how many kilograms of ammonia we could make with that (assuming we have unlimited amounts of hydrogen).
To calculate this, we first need to know how many moles of nitrogen gas are in 1 kg. For that conversion, we use the molar mass of nitrogen gas, which is 28.0 grams per mole. So, 1kg of nitrogen times 1,000 grams per 1 kg times 1 mole of nitrogen per 28 grams of nitrogen equals 35.7 moles of nitrogen.
\(1.00\text{ kg }N_2(\frac{1000 \text{g}}{1\text{ kg}})(\frac{1\text{ mol }N_2}{28.0\text{ g }N_2})=35.7\text{ moles }N_2\)
Now that we have the moles of nitrogen, we must convert to moles of ammonia. And here we use our mole ratio. 35.7 moles of nitrogen times 2 moles of ammonia over 1 mole of nitrogen equals 71.4 moles of ammonia.
\(35.7\text{ moles }N_2(\frac{2\text{ mol }NH_3}{1\text{ mol }N_2})=71.4\text{ moles }NH_3\)
And lastly, we convert the moles of ammonia to kilograms of ammonia with its molar mass, which is 17.0 grams per mole. So, 71.4 moles of ammonia times 17 grams of ammonia over 1 mole of ammonia times 1 kg over 1,000 grams equals 1.21 kg of ammonia.
\(71.4\text{ moles }NH_3(\frac{17.0\text{ g }NH_3}{1\text{ mol }NH_3})(\frac{1\text{ kg}}{1000\text{ g}})=1.21\text{ kg }NH_3\)
So, using the mole ratio, we were able to calculate that 1 kg of nitrogen can make 1.21 kg of ammonia.
Now, pause the video and take a minute to calculate how many grams of hydrogen would be needed to make 500 grams of ammonia, assuming that nitrogen is in excess. The molar masses of ammonia and hydrogen are 17 g/mol and 2 g/mol, respectively.
Hopefully, that felt pretty straightforward (if not- don’t worry, we have some more practice coming soon). Here’s how we solved that problem.
\(500\text{ g }NH_3(\frac{1\text{ mol }NH_3}{17.0\text{ g }NH_3})(\frac{3\text{ mol }H_2}{2\text{ mol }NH_3})(\frac{2.00\text{ g }H_2}{1\text{ mol }H_2})=88.2\text{ g }H_2\)
Begin with 500 grams of ammonia, convert to moles with the molar mass, then convert to moles of hydrogen with the mole ratio, and finally, convert to grams of hydrogen with the molar mass of hydrogen. That gives us 88.2 grams of hydrogen needed to make 500 grams of ammonia.
Alright, before we look at a practice problem, let’s quickly review what we’ve learned.
Mole ratios are used to convert between moles of different species in a given chemical reaction. Always make sure that your chemical reaction is balanced because mole ratios are derived from the stoichiometric coefficients. So if the reaction isn’t balanced, you won’t get the correct mole ratios!
Now try your hand at this problem:
For the combustion of propane, answer the following questions
\(C_3H_8+5O_2→3CO_2+4H_2O\)
1. What is the mole ratio between oxygen and water?
2. If you burned 10 moles of propane, how many moles of carbon dioxide would you emit into the atmosphere?
3. If you wanted to combust 1 lb of propane, how many moles of oxygen would you need?
(1.00 lb = 454 grams, and the molar mass of propane = 44.1 g/mol)
Go ahead and pause the video now if you want to try this one on your own.
Alright, here’s how you should approach this.
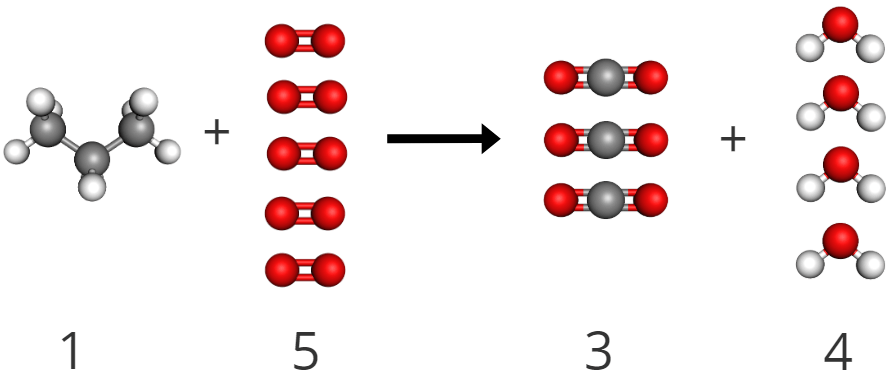
First, check to make sure that the reaction was balanced- which it was.
1. Then, to find the mole ratio between oxygen and water, simply use the stoichiometric coefficients to show that for every 5 moles of oxygen that you combust, you produce 4 moles of water.
\(\frac{5\text{ mol }O_2}{4\text{ mol }H_2O}\) or \(\frac{4\text{ mol }H_2O}{5\text{ mol }O_2}\)
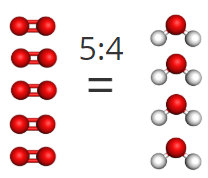
2. To convert moles of propane to moles of carbon dioxide, you need to use their mole ratio. In this case, for every mole of propane, you produce 3 moles of carbon dioxide.
\(\frac{3\text{ mol }CO_2}{1\text{ mol }C_3H_8}\)
Since you started with 10 moles of propane, this means you would produce 30
moles of carbon dioxide.
\(10\text{ mol }C_3H_8(\frac{3\text{ mol }CO_2}{1\text{ mol }C_3H_8})=30\text{ mol }CO_2\)
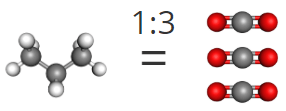
3. And lastly, to answer the third question, we convert pounds of propane to grams of propane, then to moles of propane. We then use the mole ratio to convert to moles of oxygen needed.
\(1.00\text{ lb }C_3H_8(\frac{454\text{ g}}{1\text{ lb}})(\frac{1\text{ mol }C_3H_8}{44.1\text{ g }C_3H_8})(\frac{5\text{ mol }O_2}{1\text{ mol }C_3H_8})=51.5\text{ mol }O_2\)
This shows us that we would need 51.5 moles of oxygen to react with 1 lb of propane.
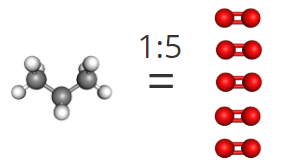
Okay, that’s all for our review of mole ratios! Thanks for watching, and happy studying!