Common Ion Effect

Hi, and welcome to this video on the common-ion effect! Let’s start with a quick review of chemical equilibrium and Le Châtelier’s principle before jumping into some examples.
First, remember that, for most chemical reactions, not all of the reactants convert to the products. The exact ratio reached between reactants and products is described by the equilibrium constant, \(K_{eq}\) ,
which is determined by the energetics of the reaction and is also defined by the temperature and Gibbs free energy of the system.
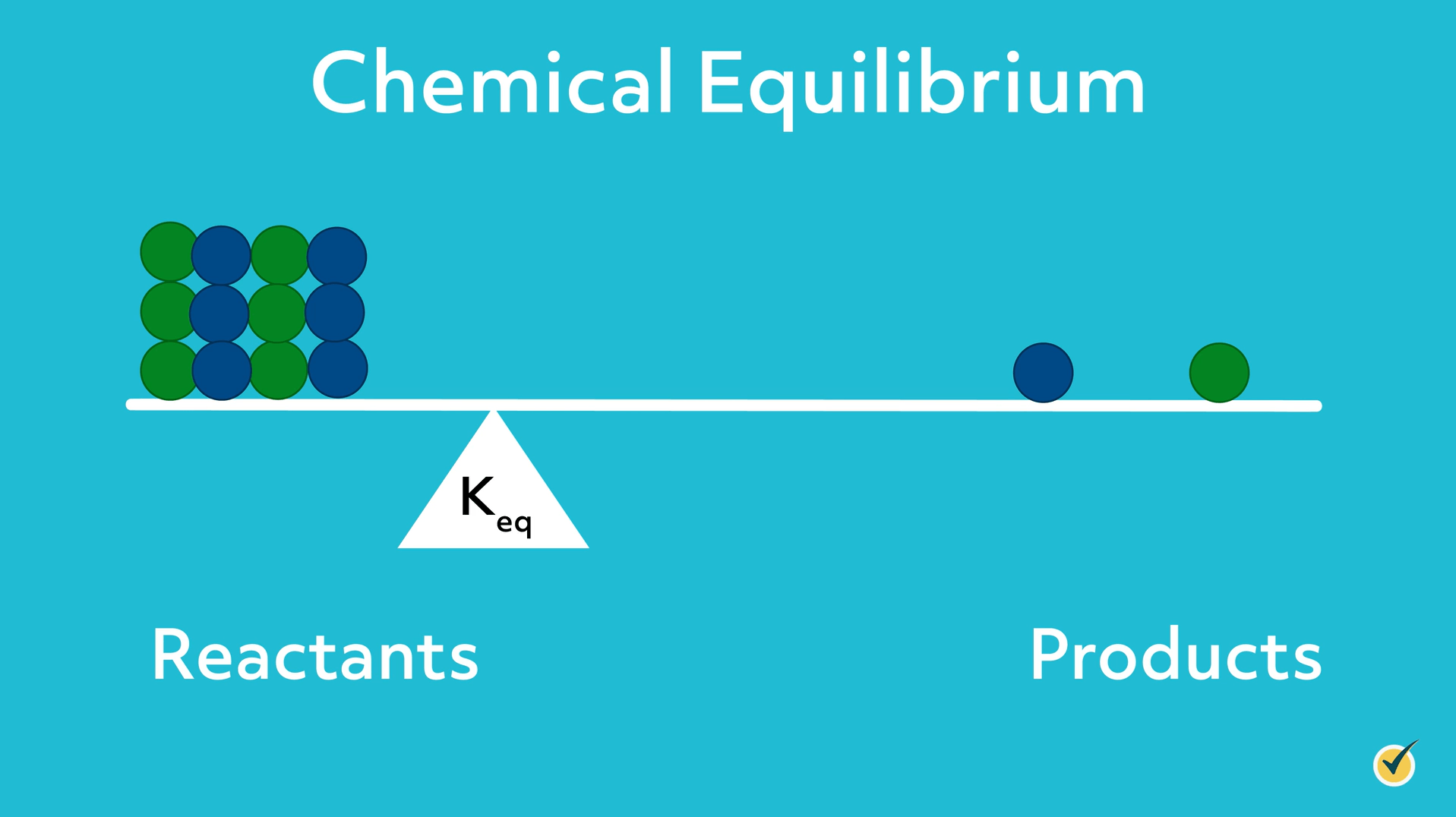
A simple and useful analogy for chemical equilibrium that we’ll use for this video is the seesaw.
Imagine that the left side represents reactants and the right side represents products.
The position of the fulcrum (the balance point) is determined by the equilibrium constant.
As the equilibrium constant increases, the fulcrum shifts to the right, and the system is balanced when there is more product than reactant.

As the equilibrium constant decreases, the fulcrum shifts to the left, and the system is balanced when there is more reactant than product.
When an external force disturbs the dynamic equilibrium, Le Châtelier’s principle describes the tendency of a system to react in a way that reduces the effect of the disturbance and re-attains balance.
So let’s say we have a system at equilibrium and we add more product.
Our system is no longer balanced and to correct this, some product is converted back to reactant.
Remember, the position of the balance point can’t change because it is defined by the equilibrium constant, which is defined by the temperature and energetics of the specific chemical reaction, neither of which have changed.
We have essentially just described the common-ion effect in general terms. More specifically though, the common-ion effect applies to aqueous solutions of weak acids and bases, as well as sparingly soluble salts. The additional product that throws the system out of balance comes from a common ion from a strong acid, strong base, or soluble salt. Let’s walk through an example to see how this actually works in practice.
When salt is added to a solution, some of it will dissolve. How much of the salt dissolves is related to the solubility constant, which sets the placement of the fulcrum. Enough salt will dissolve to maintain equilibrium.
Adding a salt that is 100% soluble in water will create a huge influx of one of the ions: the common ion. The solubility constant does not change (in other words, the fulcrum does not move), so the only way to restore balance is to convert some of the dissolved ions back to solid salts.
Say we have a \(0.1\text{ M}\) solution of acetic acid (a weak acid) in water.
Remember, a weak acid only partially dissociates in a solution and that equilibrium is described by the acid dissociation constant, \(K_a\), a special form of the standard equilibrium constant, \(K_eq\) .
\(K_a\) equals \(1.8\times{10}^{-5}\) for acetic acid, so we can start by calculating how much acid would initially dissociate in a \(0.1\text{ M}\) solution. In other words, we can calculate the equilibrium concentrations.
We know the initial concentration of acetic acid is 0.1 M and that to start, there is no concentration of the two ions. However, these concentrations will change as the system reaches equilibrium. The acetic acid concentration will drop by \(x\) and the concentrations of the two ions will increase by \(x\).
| \(CH_{3}COOH\) | \(CH_{3}COO^{-}\) | \(H^{+}\) | |
|---|---|---|---|
| Initial | \(0.1M\) | \(0\) | \(0\) |
| Equilibrium | \(0.1-x\) | \(x\) | \(x\) |
To simplify our calculation, we can assume that \(x\) is much smaller than 0.1 (meaning that we assume very little acid will dissociate), and then solve the equation to show that \(x=0.0013\), which means that of the original 0.1 M of acetic acid, \(0.0013\text{ M}\) dissociated into acetate and hydrogen ions, or about 1.3%.
Note also, that our assumption that \(x\), \(0.0013\), would be much smaller than 0.1, was true. This is an assumption that we make frequently in weak acid problems, but it’s always good to check yourself.
Now, let’s consider what happens when we add sodium acetate to our solution of acetic acid.
When added to water, sodium acetate completely dissolves into sodium and acetate ions.
As we know, acetic acid also dissociates into the acetate ion, so our two reactions have a common-ion!
Let’s go back to our seesaw.
By adding sodium acetate, we increase the concentration of acetate ions to \(0.1\text{M}\) in our solution, which we must take into account when calculating the equilibrium for acetic acid- even though it came from a different source.
The equilibrium for acetic acid is now out of balance. Remember, \(K-{a}\) maintains the same numeric value, and thus, the only way to rebalance the system is to convert some products back to reactants.
In this case we have zero point one molar plus \(x\) times \(x\) divided by zero point one molar minus \(x\) which is again equivalent to zero point one molar times \(x\) divided by zero point one molar. This means that \(x\) is equal to one point eight times ten to the negative five.
\(=\frac{\left ( 0.1M+x \right )\left ( x \right )}{\left ( 0.1M-x \right )}=\frac{\left ( 0.1M+x \right )\left ( x \right )}{\left ( 0.1M \right )}\)
| \(CH_{3}COOH\) | \(CH_{3}COO^{-}\) | \(H^{+}\) | |
|---|---|---|---|
| Initial | \(0.1\text{ M}\) | \(0.1\text{ M}\) | \(0\) |
| Equilibrium | \(0.1\text{ M}-x\) | \(0.1\text{ M}+x\) | \(x\) |
To make the calculation easier, we’re going to assume that none of our acetic acid has dissociated yet, so we begin with \(0.1\text{M}\) concentrations of acetic acid and acetate. This allows us to quickly solve for \(x\), the hydrogen ion concentration, as being \(0.000018\text{M}\), which is two orders of magnitude smaller than what it was without adding sodium acetate! This means that much less acetic acid dissociated in the presence of sodium acetate.
And while these numbers may seem small, that change in hydrogen ion concentration would raise the pH from 2.89 to 4.74! All done by just adding a common ion to the solution!
So in summary, adding a common ion shifted the equilibrium to the left, meaning the system needed more reactant and less product to achieve balance. Another common way of phrasing this is that adding a common ion suppresses the dissociation of a weak acid. We could have achieved the same result by adding a strong acid, but in that case, the common ion would have been hydrogen.
As a side note, if that whole process reminded you of buffers, you are totally on the right track! Many buffers are made by combining an acid and its conjugate base- like we just did- which makes buffers a great practical example of the common-ion effect!
I hope this review was helpful! Thanks for watching, and happy studying!