Calculating Volumes Using Integration

As we have seen before, integrals are helpful for determining the area beneath curves that lie on two-dimensional planes—but did you know that integrals can also be used to find the volumes of shapes in three-dimensional spaces?

Let’s say I was interested in finding the volume of an apple. One way I could do that is by cutting the apple into very thin slices, each one approximately 1 millimeter thick.

Then I could find the area of each slice’s cross section, multiply each area by its one-millimeter thickness to get an approximation of the volume of each slice, then add all the slices’ approximate volumes together. Of course, this method would give me the volume of something more like this, with choppy edges:

…but it works nicely as an approximation for the apple’s volume. When finding the volume of a shape or object with calculus, it is helpful to think of slicing the shape into very thin slices and finding the area of each slice’s cross section. By using integration though, we can think of each slice as being infinitely thin, so that the volume obtained is the true volume of the shape and not just a blocky approximation.

In order to obtain the volume of a shape using integration, you’ll need a formula for the shape’s cross-sectional area in terms of one variable. Whichever variable the area function is in terms of (whether \(x\), \(y\), or \(z\)), that is the axis which the cross sections will be perpendicular to. This area function will then be integrated in terms of that variable, and the bounds of the integral will be two starting and ending values for that same variable.

For example, if we wanted to find the volume of this shape using integration, we may choose to cut cross sections perpendicular to the \(z\)-axis. In this case, we would need to write a function of the cross sections’ areas in terms of \(z\), and then integrate that area between the bounds \(z=-2\) to \(z=2\) since the shape begins and ends at those height boundaries.

Let’s find the volume of this shape now. The equation of this ellipsoid is \(4x^{2}+4y^{2}+z^{2}=4\). Since we are going to “cut slices” perpendicular to the \(z\)-axis, we need to write a function of the cross-sectional area in terms of \(z\).

Notice that our slices, perpendicular to the \(z\)-axis, will be circular in shape. What do we know about the area of circles? We know that the area of a circle is equal to pi times the radius squared. Now we need a way of writing this in terms of the variable \(z\).

If we move \(z^{2}\) to the right-hand side of the ellipsoid equation, we’ll get:

Now, recall that the equation of a circle with radius \(r\) is \(x^{2}+y^{2}=r^{2}\). We can get something very similar by dividing both sides by 4:

What we have now is still the equation of the ellipsoid, but now the right side of the equation is exclusively in terms of \(z\). Additionally, since the left side equals \(x^{2}+y^{2}\), the right side is equivalent to \(r^{2}\) in the equation of a circle—in this case, the equation of the circles we are cutting from the ellipsoid.

And we can use this to write the area function in terms of \(z\).

This function represents the area of the cross section of the circular slices of the ellipsoid. Now that we have this function, we can build the definite integral to obtain the volume of the ellipsoid.

Based on the graph, we know that the ellipsoid’s lowest point is at \(z=-2\) and that its highest point is at \(z=2\). If we didn’t have the graph available to look at though, we could solve for this by setting \(x\) and \(y\) equal to zero in the equation of the ellipsoid. Let’s input positive and negative 2 as the bounds of integration.

Now, since \(\pi\) and the 4 in the denominator are both constants, we can move them outside the integral.

Then \(-z^{2}\) integrates to \(-\frac{1}{3}z^{3}\), and 4 integrates to \(4z\).

Plugging in the bounds at negative 2 and positive 2, we get:

Then we can simplify this a little bit.

Since we are describing volume, this solution would be in units cubed.

Let’s try another problem now. Madalyn is using a 3D printer to create a shape which is 2 centimeters tall at all points, and which has a footprint in the shape of the area between the curve \(y_{1}=\frac{1}{2}x^{2}-x+\frac{1}{2}\) and the line \(y_{2}=3\) on the domain \(0\lt x\lt 3\), expressed in centimeters.

What is the volume, in centimeters cubed, of this shape?

This kind of problem can be tricky to understand if you don’t have a visualization of the shape, so let’s graph the area between the lines \(y_{1}\) and \(y_{2}\) on the domain \(0\lt x\lt 3\).

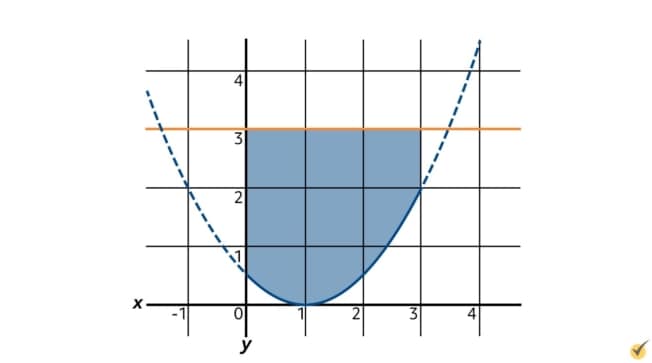
This area describes the footprint of Madalyn’s shape, meaning this is what the shape looks like if you look down at it from directly above. To illustrate what Madalyn’s shape looks like in three dimensions, we can draw this graph at a slant and add in the \(z\)-axis. Remember, the height of the shape—which is the measurement along the \(z\)-axis—equals 2 centimeters at all points, so the shape would look something like this:

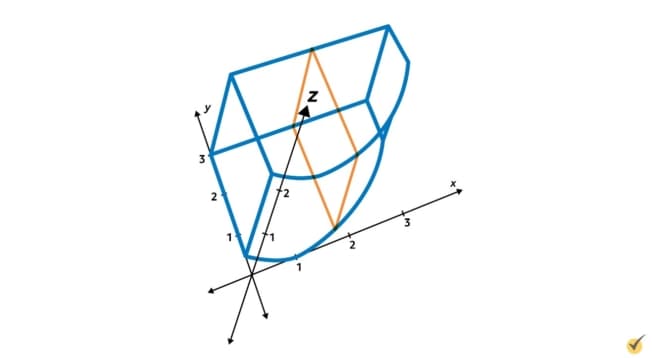
Now since the lines \(y_{1}\) and \(y_{2}\) are written in terms of \(x\), let’s see if we can cut this shape into slices perpendicular to the \(x\)-axis. Such slices would look something like this:

These slices are each in the shape of rectangles, and each rectangle has a height of 2 centimeters since the shape has a fixed height. The width of each rectangle is equal to the distance between \(y_{1}\) and \(y_{2}\). Since \(y_{2}=3\) is above the curve \(y_{1}\), this distance can be written as \(y_{2}-y_{1}\). We can easily calculate the area of each rectangle by multiplying \(y_{2}-y_{1}\) by 2.

Now since we know that \(y_{2}=3\), and \(y_{1}=\frac{1}{2}x^{2}-x+\frac{1}{2}\), we can plug these functions in.

Now that we have a function for the cross-sectional area of each slice, we need to take its integral. What are the bounds for this integral? Since we have area in terms of \(x\), and will be integrating in terms of \(x\), we need to check the bounds of the shape in terms of \(x\). We are told in the problem statement that the domain for the shape is \(0\lt x\lt 3\), so the bounds for the definite integral will be 0 and 3.

Taking this integral, we get:

Then, if we do that evaluation, we’ll get:

If we plug all this into a calculator, we’ll get \(15-0\). So the volume of Madalyn’s shape is then equal to \(15-0=15\) centimeters cubed.

Let’s work through one more example. Consider the area bounded between the curves \(x_{1}=\frac{1}{4}y^{2}\) and \(x_{2}=\frac{1}{4}y+3\) between the bounds \(y=0\) to \(y=3\). A three-dimensional shape, whose footprint is this area, is shaped in such a way that its cross section, when cut perpendicular to the \(y\)-axis, is an equilateral triangle whose base lies flat on the \(xy\)-plane. Find the volume, in units cubed, of this shape. (Hint: the area of an equilateral triangle is equal to the square root of 3 over 4 times the side length squared.)

Let’s begin by drawing the area between \(x_{1}\) and \(x_{2}\) on the \(xy\)-plane, and then visualizing what the 3D shape looks like.

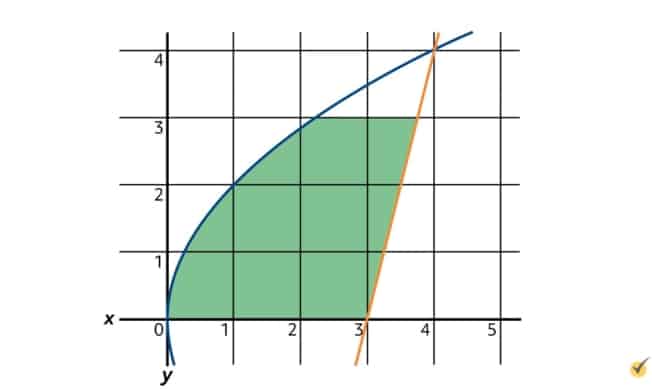
\(x_{1}=\frac{1}{4}y^{2}\) is shaped like a sideways parabola, while \(x_{2}=\frac{1}{4}y+3\) is an upward-sloping straight line. The area between these curves from \(y=0\) to \(y=3\) is shaped somewhat like a shark fin.

In terms of this shape’s 3D appearance, we are told that its cross section, when cut perpendicular to the \(y\)-axis, is an equilateral triangle whose base is on the \(xy\)-plane. So we can draw the shape in this way:

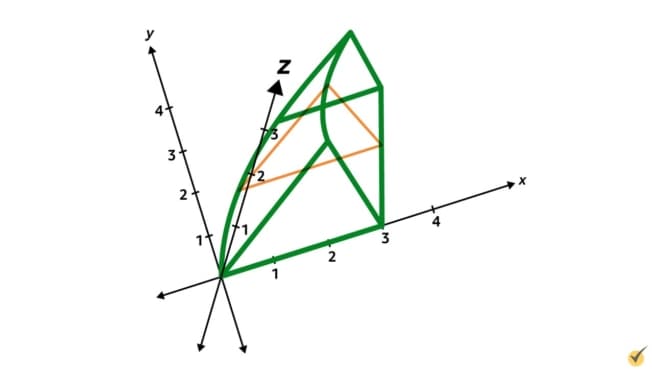
Now, we know that we are going to need to do an integral to find the volume of this shape. And before we can do the integral, we need a function of area in terms of one variable. In this case, since we know that the slices will be cut perpendicular to the \(y\)-axis, we are going to want the area of each cross section written in terms of y.

Remember, the area of an equilateral triangle equals \(\frac{\sqrt{3}}{4}\) times the length of the side squared. We can find that side length by finding the distance between the two curves \(x_{1}\) and \(x_{2}\). Since \(x_{2}\) is farther to the right and therefore has greater x-values, we will write this distance as \(x_{2}-x_{1}\), or \((\frac{1}{4}y+3)-(\frac{1}{4}y^{2})\).

Writing this in descending order, the side length of each triangular slice equals \(-\frac{1}{4}y^{2}+\frac{1}{4}y+3\). We can now write the area function in terms of \(y\) as:

The bounds of integration for this shape will be at \(y=0\) and \(y=3\), as mentioned in the problem statement. Let’s write the definite integral now:

To make this integral easier for ourselves, let’s move the constant \(\frac{\sqrt{3}}{4}\) in front of the integral, and expand the squared expression inside.

Now, taking the integral, we get:

Since each of these terms has a multiple of \(y\), we know that evaluating at 0 will just give us 0. So we just need to evaluate at 3

If we plug this into a calculator, we’ll get approximately 9.23 cubic units.

As we’ve seen, problems where you need to find volume with integration can be daunting at first glance. However, you should find it helpful to start by sketching what the shapes look like. Then, decide which axis your slices will be perpendicular to, and write an area function in terms of that variable. Finally, integrate this area function and evaluate it at the appropriate bounds to determine the shape’s volume in cubic units. As always, this gets easier with practice, so I encourage you to try some example problems on your own now.

Thanks for watching, and happy studying!