Calculating Distances Using Integration

Because of the special relationship that the position, velocity, and acceleration of an object have with each other, if we have information only about one of these metrics, we can use integrals and derivatives to determine the other two. In this video, we are going to discuss how to use this logic to calculate displacement and distance traveled by an object using information about its velocity.

If we think of velocity as a rate of change in an object’s position, then we can understand that the object’s velocity can be found by taking the derivative of the object’s position function.

Conversely, if we have the object’s velocity function \(v(t)\), we can get the position function by taking the integral of \(v(t)(\int v(t)dt)\). If the integral is bounded to specific starting and ending times, then the solution is a number describing the displacement of the object over that time.

For example, if a tire starts rolling down a hill with the velocity function \(v(t)=\frac{3}{2}t\), where \(t\) is in seconds and velocity is in feet per second, we can determine its position function by taking the indefinite integral of \(v(t)\).

\(s(t)=\int v(t) dt=\int \frac{3}{2}t\text{ }dt\)

Here, we can move the three-halves out front and handle \(t\) separately.

\(\frac{3}{2}t\text{ }dt\)

We raise the power of \(t\) by one, and divide it by the new power.

\(\frac{3}{2}\cdot \frac{1}{2}t^{2}+C\)
 
\(\frac{3}{4}t^{2}+C\)

So the tire’s position function (which is usually called \(s(t)\)) equals \(\frac{3}{4}t^{2}\) plus a constant. If we wanted to find out how far the tire rolled from, say, \(t=1\) sec to \(t=3\) sec, we would use a definite integral with an upper bound of 3 and lower bound of 1:

\(\int_{1}^{3}v(t)dt\)
 
\(=\frac{3}{4}\text{ }t^{2}\text{ } |_{1}^{3}\)
 
\(=\frac{3}{4}(3)^{2}-\frac{3}{4}(1)^{2}\)
 
\(=\frac{3}{4}(9)-\frac{3}{4}(1)\)
 
\(=\frac{27}{4}-\frac{3}{4}\)
 
\(=\frac{24}{4}=6\)

So the tire would have moved a distance of six feet from \(t=1\) sec to \(t=3\) sec.

Now, at the beginning of this video I mentioned that we are interested in finding displacement and distance traveled. Let’s quickly make a distinction between the two.

Consider a pendulum swinging in a clock. The pendulum starts at the left of its arc, and each second, swings to the right and then back. If we watch the pendulum for exactly five seconds, the pendulum will end up exactly where it started—at the left of its arc. This means the displacement, or net change in position, of the pendulum comes out to zero. The distance traveled by the pendulum, however, is equal to five times the distance swung back and forth each second.

So if the clock’s pendulum swings six inches to the right and then six inches back to the left each second, it moves a distance of twelve inches, or one foot per second, and sixty inches, or five feet after five seconds. For distance traveled, we add all of these lengths together, even though some are in opposite directions.

With displacement on the other hand, we would add six inches each time the pendulum moves to the right, but subtract six inches each time the pendulum swings to the left. This would result in a net zero inches each second. For displacement, direction—and therefore signs—matter.

Let’s put this new knowledge to work on a velocity problem now.

Ashton is driving to visit family, but along the way he realizes he left his wallet at home. He returns home, grabs it, then begins driving again. Ashton’s velocity at t hours is given in miles per hour by the function \(v(t)=50\text{ }sin(\pi t)\). \(v(t)\) is negative when Ashton is driving back towards home, then positive again when he is driving toward his family. Find Ashton’s displacement from \(t=0\) to \(t=3\), then find his distance traveled over the same time.

First, we want to know about Ashton’s displacement over the given time interval. Remember, displacement is essentially the net change in position, so the “negative area” we get when Ashton is driving back home is offset by the positive area we get when he drives toward his family. To calculate his displacement, we simply need to take the integral of \(v(t)\) on the time bounds given.

\(\int_{0}^{3}\text{ }50 sin (\pi t)\text{ }dt\)

Since 50 is a constant, we can pull that out to the front of the integral.

\(50 \int_{0}^{3} sin (\pi t)\text{ }dt\)

Then we can do u-substitution:

\(u=πt\)
 
\(du=π\text{ }dt\)
 
\(dt=\frac{1}{π}\text{ }du\)

Now we can go back to our previous function and plug some things in.

\(50 \int_{0}^{3} sin (u)\cdot \frac{1}{\pi}\text{ }du\)

We need to make sure we have a \(du\) instead of a \(dt\) because our function is now in terms of \(u\). Now, pull out \(\frac{1}{π}\) since it’s a constant.

\(50 \cdot \frac{1}{\pi}\int_{0}^{3} sin (u) \text{ }du\)
 
\(50 \cdot \frac{1}{\pi}[-cos (u)]|_{0}^{3}\)

Now we can plug in our u-value and bring things back into terms of t.

\(50 \cdot \frac{1}{\pi}[-cos (\pi t)]|_{0}^{3}\)

Then, evaluating from 0 to 3 we have

\(\frac{50}{\pi}[-cos (3\pi)-(-cos(0))]\)
 
\(\frac{50}{π}[1+1]\)
 
\(\frac{50}{\pi}(2)=\frac{100}{π}\)

Since velocity was given in miles per hour, and \(t\) represents hours passed, this solution is given in miles. So Ashton’s displacement after three hours is \(\frac{100}{\pi}\) miles.

Let’s now determine his distance traveled. For this, we are going to consider his “negative miles” to be positive. More practically, we are going to take the integral again, but we must chop the domain into sections.

The first section will be the “positive miles” that Ashton travels before turning around; and the second will be the time where he is driving back home. This second section’s area will be negated, or subtracted, so that it turns out positive overall. Finally, the third section of the domain will be the time where Ashton is pointed in the right direction again. To find these turning points, we need to solve for where the velocity is equal to zero.

Before we do that I’m going to write down our position and velocity functions so we can reference them later. So, remember, our position function comes from integrating our velocity function. So that’s what we got down here without paying attention to the 0 to 3 part because that was for our integration specifically. So if we simplify this a little bit we have \(50\cdot \frac{1}{π}\cdot (-1)\), because of the negative cosine.

So that can simplify to:

\(s(t)=-\frac{50}{π}cos(πt)+C\)

So this is our position function, and then remember, our velocity function is what we took the integral of earlier.

\(v(t)=50sin(πt)+C\)

Now let’s go ahead and find where our velocity is equal to 0.

\(v(t)=50sin(\pi t)=0\)

Dividing both sides by 50, we get \(sin(\pi t)=0\). From the unit circle, we know that the only places sine equals zero are at 0 and \(π\) radians, so:

\(\pi t=0\) and \(\pi t=\pi\)
 
\(\frac{\pi t}{π}=\frac{0π}{ }\) and \(\frac{tπ}{\pi}=\frac{π}{\pi}\)
 
\(t=0\) and \(t=1\)

This gives us \(t=0\) and \(t=1\). But \(t=0\) is the beginning of our considered time period, and doesn’t help us much. Notice, however, that \(t=2\) also makes \(sin(\pi t)\) go to zero, and is between 0 and 3. This tells us that our “turning points” happen at \(t=1\) and \(t=2\).

Our integral for determining Ashton’s distance traveled is then chopped into sections like this:

\(\int_{0}^{3}|v(t)|dt=\int_{0}^{1}v(t)dt-\int_{1}^{2}v(t)dt+\int_{2}^{3}v(t)dt\)

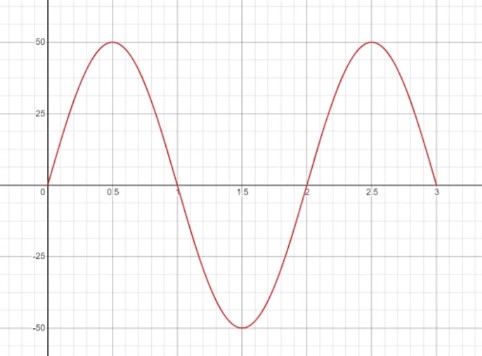
Notice that each positive “chunk” corresponds to the parts of the velocity function that are positive, while the negative “chunk” corresponds to the part of the velocity function that is negative. Let’s work out our solution now. We previously determined that the integral of \(50sin(\pi t)\) is \(-\frac{50}{π} cos(\pi t)\), so we can plug that right in:

\(\int_{0}^{3}|v(t)|dt=-\frac{50}{\pi}cos(\pi t)|_{0}^{1}- -\frac{50}{\pi}cos(\pi t)|_{1}^{2}+ -\frac{50}{\pi}cos(\pi t)|_{2}^{3}\)

This might look busy, but since \(cos(n\pi )\), where \(n\) is any integer, equals either positive or negative one, it should all boil down nicely enough:

\(-\frac{50}{\pi}(cos(\pi))-cos(0))-(-\frac{50}{\pi})(cos(2\pi)-cos(\pi))+(-\frac{50}{\pi})(cos(3\pi))-cos(2\pi))\)

Now we can simplify a little bit.

\(-\frac{50}{\pi}(-1-1)-(-\frac{50}{\pi})(1-(-1))+(-\frac{50}{\pi})(-1-1)\)
 
\(-\frac{50}{\pi}(-2)-(-\frac{50}{\pi})(2)+(-\frac{50}{\pi})(-2)\)
 
\(\frac{100}{\pi}+\frac{100}{\pi}+\frac{100}{\pi}-\frac{300}{\pi}\)

So after three hours, Ashton traveled a distance of \(\frac{300}{\pi}\) miles. Though, he was only displaced overall by \(\frac{100}{\pi}\) miles in that time because he forgot his wallet at home.

We now see that if we know a person’s or an object’s velocity, we can determine their position and therefore displacement and distance traveled over a period of time by integrating the velocity function. Calculating displacement is relatively simple, because you just need to integrate over the time period concerned. Finding the distance traveled requires a couple extra steps, though. First, you need to determine at what times the object’s velocity equals zero. These are the “turning points” where the domain must be separated. For each portion of the domain where the velocity is negative, the integral taken over that section must be negated, or subtracted, to turn the area positive overall.

You’ll have displacement and distance problems mastered in no time with a little practice.

Thanks for watching, and happy studying!