A line of symmetry refers to a line that is drawn through the center of a shape so that it creates two identical halves. Each half is a mirror image of the other. Some shapes have one line of symmetry, like an isosceles triangle, and other shapes have many lines of symmetry.
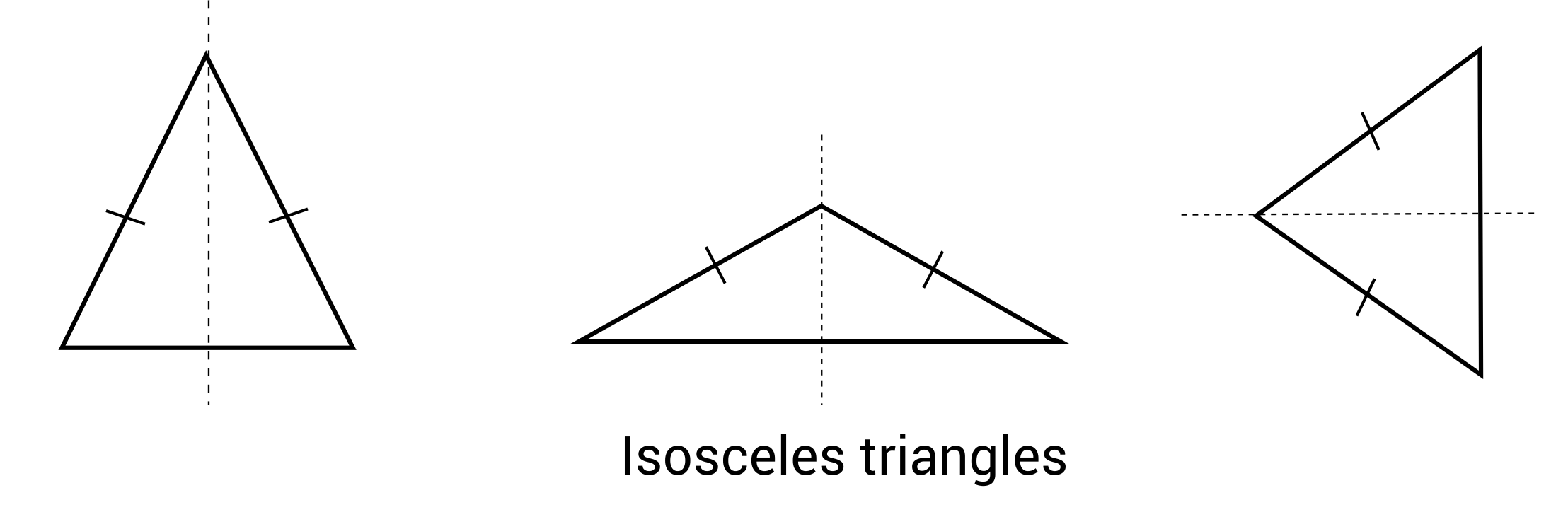
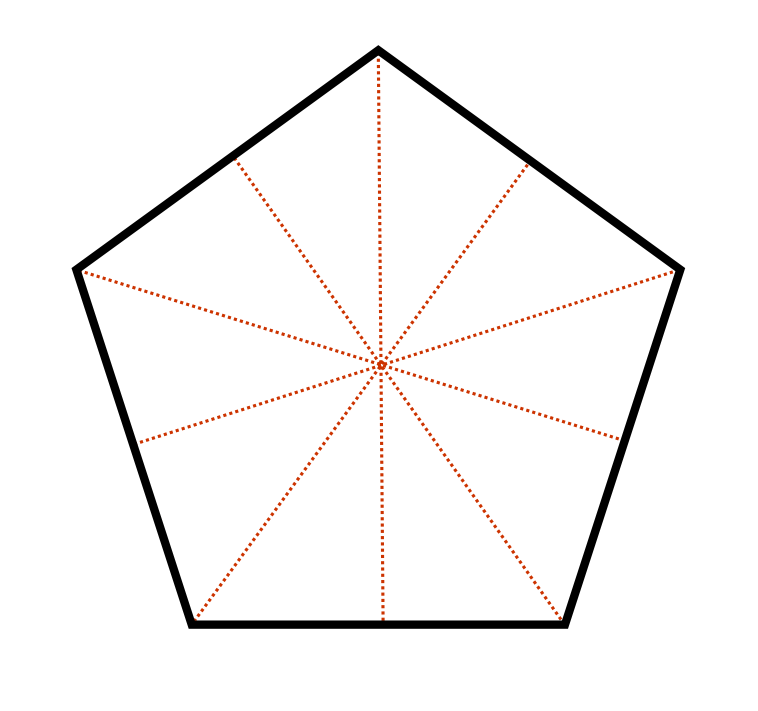
For example, a regular pentagon has 5 lines of symmetry. Not all shapes will have lines of symmetry however. Imagine the letter J. We cannot draw one line through the letter J with the result being two identical halves. Letters such as W, B, O, and Y do have lines of symmetry.

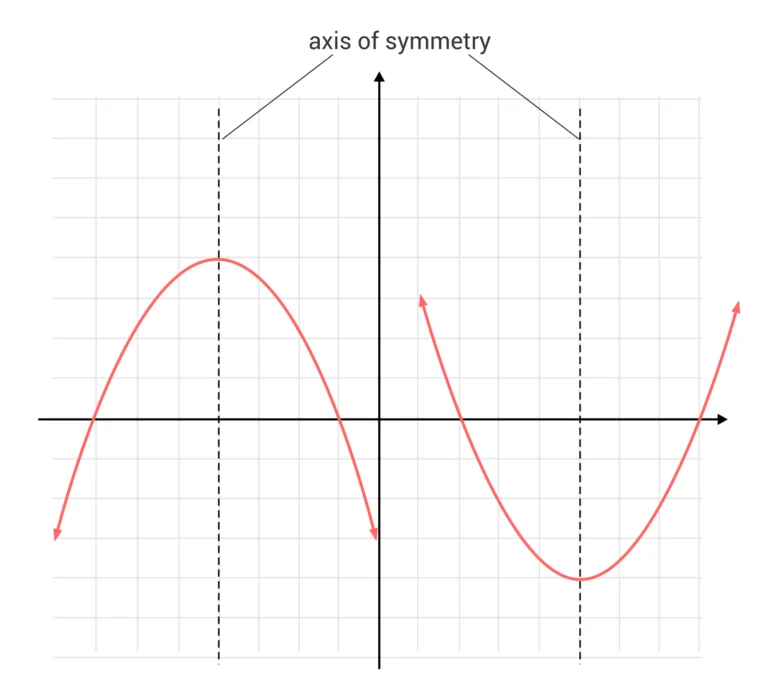
The equation of a parabola creates an arc when it is graphed. This U shape has one line of symmetry, right down the middle of the arc. This line is referred to as the axis of symmetry.
Axis of Symmetry Formula
When a parabola is graphed in standard form, we can use the formula \(x=\frac{-b}{2a}\) in order to locate the axis of symmetry. Remember that when an equation is in standard form it appears as \(y=ax^2+bx+c\). We can take the values of a and b and plug them into the formula \(x=\frac{-b}{2a}\) in order to solve for x.
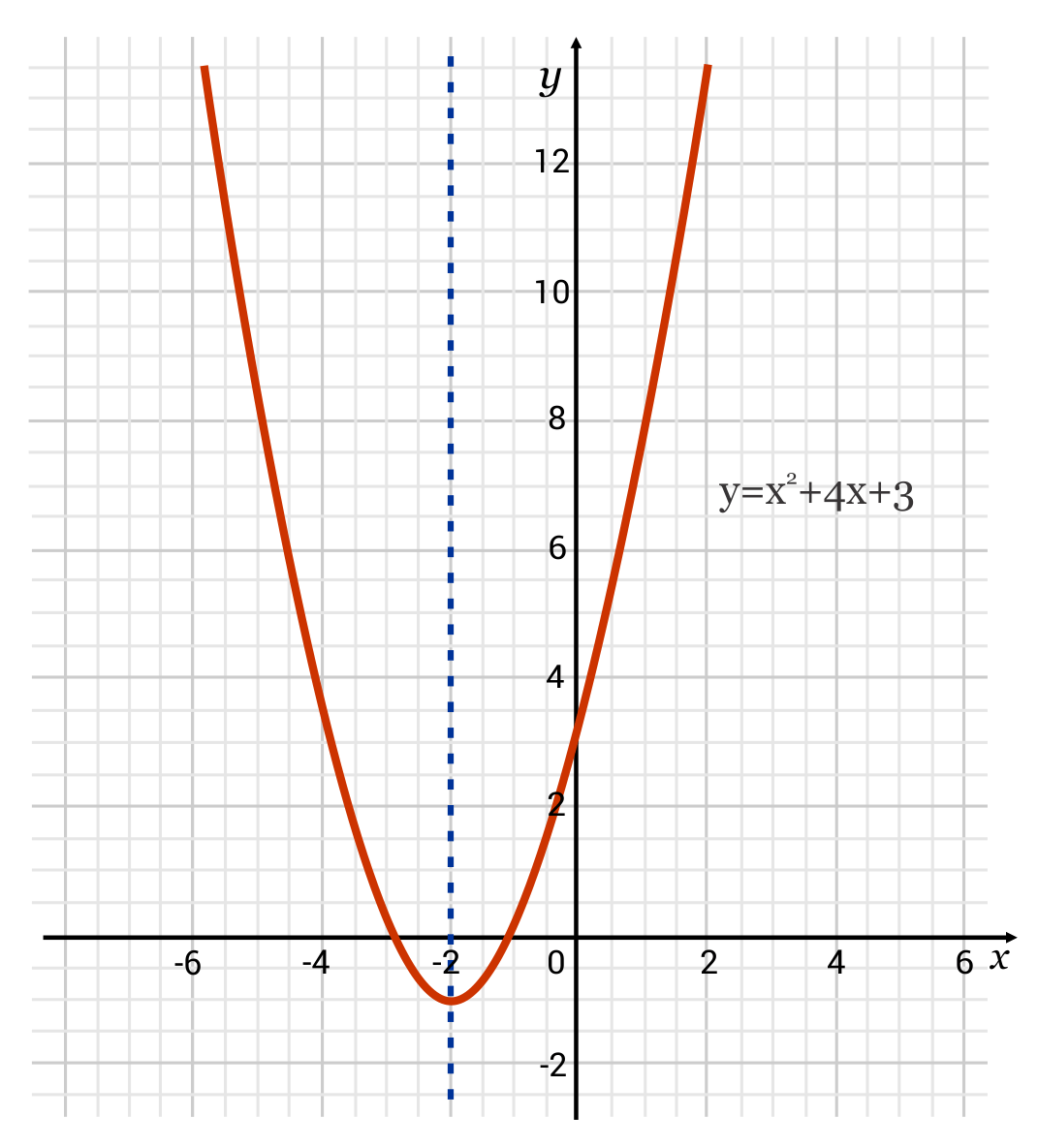
For example, if we are given the equation for a parabola in standard form such as \(y=x^2+4x+3\), we know that \(a=1\), \(b=4\), and \(c=3\). From this point we can plug in the value of a and b into the formula \(x=\frac{-b}{2a}\) in order to determine the axis of symmetry. The formula becomes \(x=\frac{-(4)}{2(1)}\) which simplifies to \(x=-2\). This means that the axis of symmetry is the vertical line passing through \(x=-2\). This line will split the parabola into two identical halves.
Parabolas that are in vertex form will also have an axis of symmetry. However, the formula is slightly different. When a parabola is given in vertex form, it appears as \(y=a(x-h)^2+k\), where h and k represent the ordered pair at the vertex of the graph. In other words, \((h,k)\) is the base point or the top point on the arc. This means that if a line is drawn vertically through this vertex, it will divide the parabola into two equal halves. Essentially, in order to determine the axis of symmetry, we simply need to identify the vertex. The formula for the axis of symmetry for a parabola in vertex form is \(x=h\).
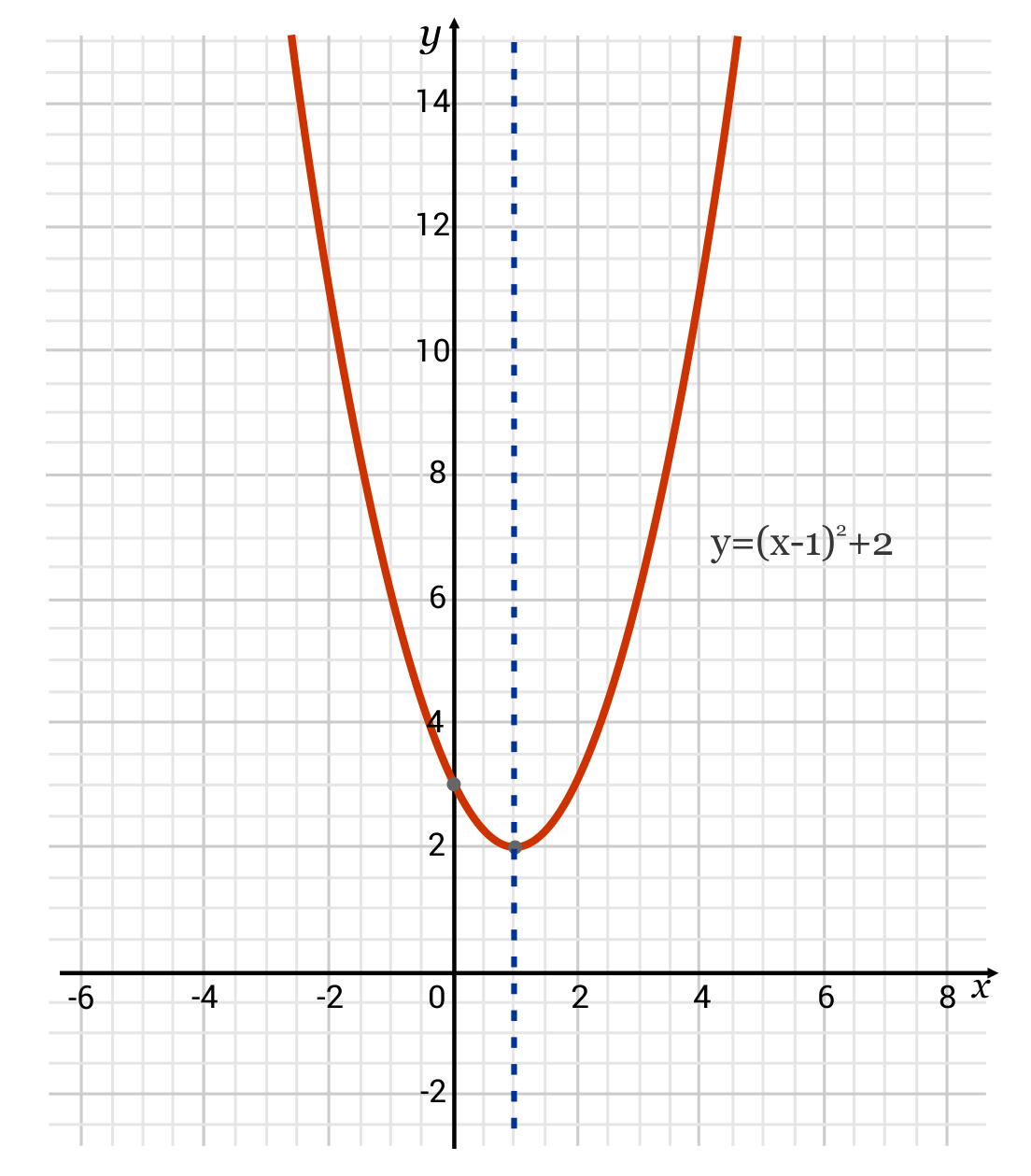
For example, if you are given \(y=(x-1)^2+2\) as the equation of a parabola in vertex form, and you need to determine the axis of symmetry, you first need to identify the vertex, and then the value of h. The vertex is \((h,k)\) when in vertex form \((y=a(x-h)^2+k)\). In the equation we can see that the value of h is represented by a 1, and the value of k is represented by a 2. This tells us that the vertex is at the point \((1,2)\). Now that we know the value of x is 1, we know that the axis of symmetry is also at 1. The vertical line drawn at \(x=1\) is the axis of symmetry.

Axis of Symmetry Sample Questions
Here are a few sample questions going over axis of symmetry.
How many lines of symmetry can be drawn on a regular pentagon?
A line of symmetry divides a figure into two equal mirror images, or halves. For a pentagon there are 5 different lines of symmetry.
What is the formula for the axis of symmetry for a parabola that is in standard form?
The axis of symmetry for a parabola is the line that will divide a parabola into two equal halves which are mirror images of each other. The formula \(x=\frac{-b}{2a}\) will locate the axis of symmetry for a parabola that is given in standard form \(y=ax^2+bx+c\).
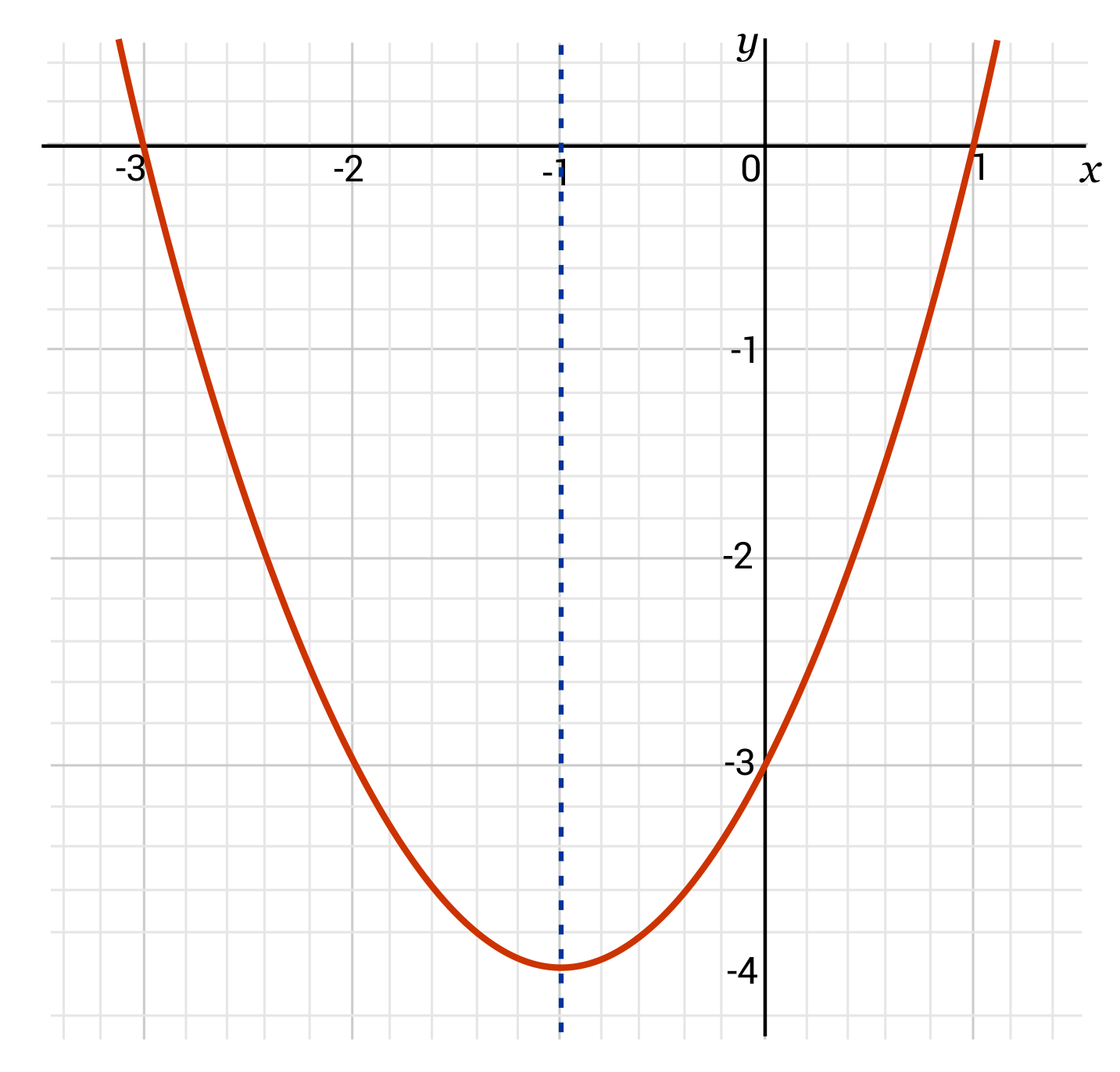
Identify the axis of symmetry for the following parabola given in standard form: \(y=x^2+2x-3\).
The equation for the parabola in standard form is \(y=x^2+2x-3\). This means that \(a=1\), \(b=2\), and \(c=-3\). We can plug these values into the formula \(x=\frac{-b}{2a}\) in order to identify the axis of symmetry. When a and b are plugged into the formula it becomes \(x=\frac{-(2)}{2(1)}\) which simplifies to \(x=-1\). The vertical line at \(x=-1\) divides the parabola into two symmetrical halves.
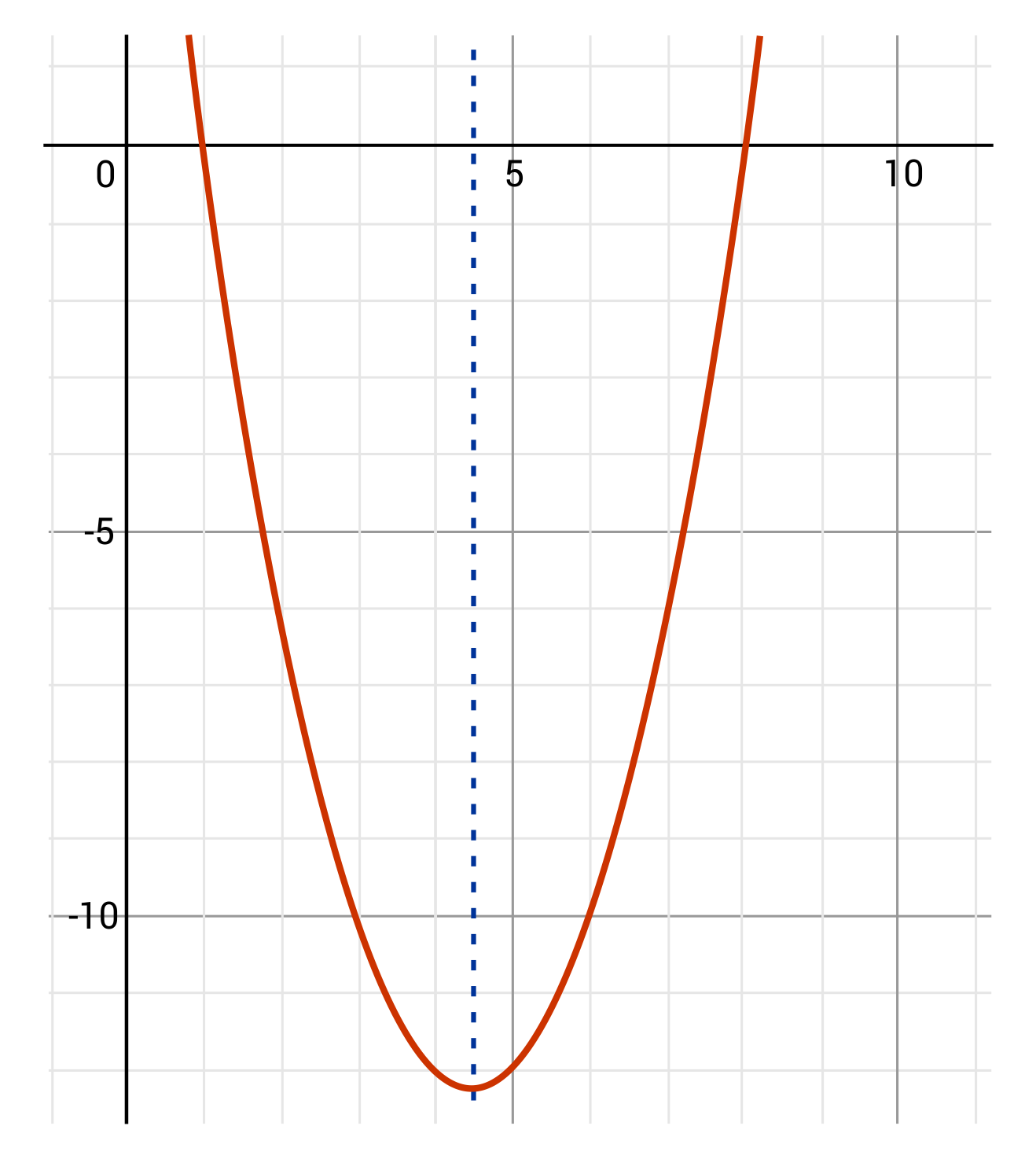
Mr. Matthews drops down into a snowboard halfpipe shaped like a parabola. The equation that matches the shape of the halfpipe is \(y=x^2-9x+8\) in standard form. Use the equation to determine the axis of symmetry.
In the equation \(y=x^2-9x+8\), \(a=1\), \(b=-9\), and \(c=8\). We can take these values and plug them into the formula \(x=\frac{-b}{2a}\) in order to find the axis of symmetry. The formula now becomes \(x=\frac{-(-9)}{2(1)}\) which simplifies to \(x=\frac{9}{2}\) or \(x=4\frac{1}{2}\).
The arc of a kicked soccer ball can be graphed using the equation \(y=-2(x-3)^2+5\) in vertex form. When graphed, this equation will form a parabola, similar to the image below. Use the equation to determine the axis of symmetry.
The equation \(y=-2(x-3)^2+5\) is in vertex form \((y=a(x-h)2+k)\). We can see that the number 3 represents h, and the number 5 represents k. This tells us that the vertex of the graph is at the point \((3,5)\). Now that we know that the value of x is 3, we know that the axis of symmetry is located at \(x=3\). The vertical line drawn at \(x=3\) will divide the graph into two identical halves.