
Hi, and welcome to this video lesson on Venn diagrams!
Venn diagrams are super helpful, because they help us understand the relationships between large groups or sets of different things. Venn diagrams were developed during the 1702 and have been used more and more ever since.
Here’s how they work. Imagine we have a set of things called “A”. Set A has a lot of different fonts for the letter A (go figure, right?). Some of those fonts can be used on the letter B. Imagine there is a set B, as well. Set B contains a bunch of fonts for the letter B.
As you can imagine, there are many fans that can be used both on the letters A and B. What do you do about them? Well, our Venn diagram provides an option. We can make set A and set B overlap, creating a third set within both of them. Let’s try a more practical example.
Imagine set A is set of numbers between 1 and 20 divisible by 2. That includes 2, 4, 6, etc. Now, imagine another set exists. All the numbers between 1 and 20 divisible by 3. That’s set B. What do we do about those numbers between 1 and 20 that are divisible by both 2 and 3?
Well, let’s diagram it. We can see that by overlapping sets A and B, we create a third set that is part of both. We can see that by overlapping sets A and B we create a whole new third subset. Venn diagrams are really helpful for helping us understand how sets interact with one another, and there’s no limit to how many sets can interact.
Take for example, this. This is a Venn diagram of four different sets. They all interact, and they create nine new subsets. Crazy, right?
I hope that helps. Thanks so much for watching this video lesson. Until next time, happy studying!
Venn Diagram Practice Questions
The following Venn diagram shows the number of students enrolled in Chemistry, Physics, or both. How many more students are exclusively enrolled in Chemistry, compared to exclusively enrolled in Physics?
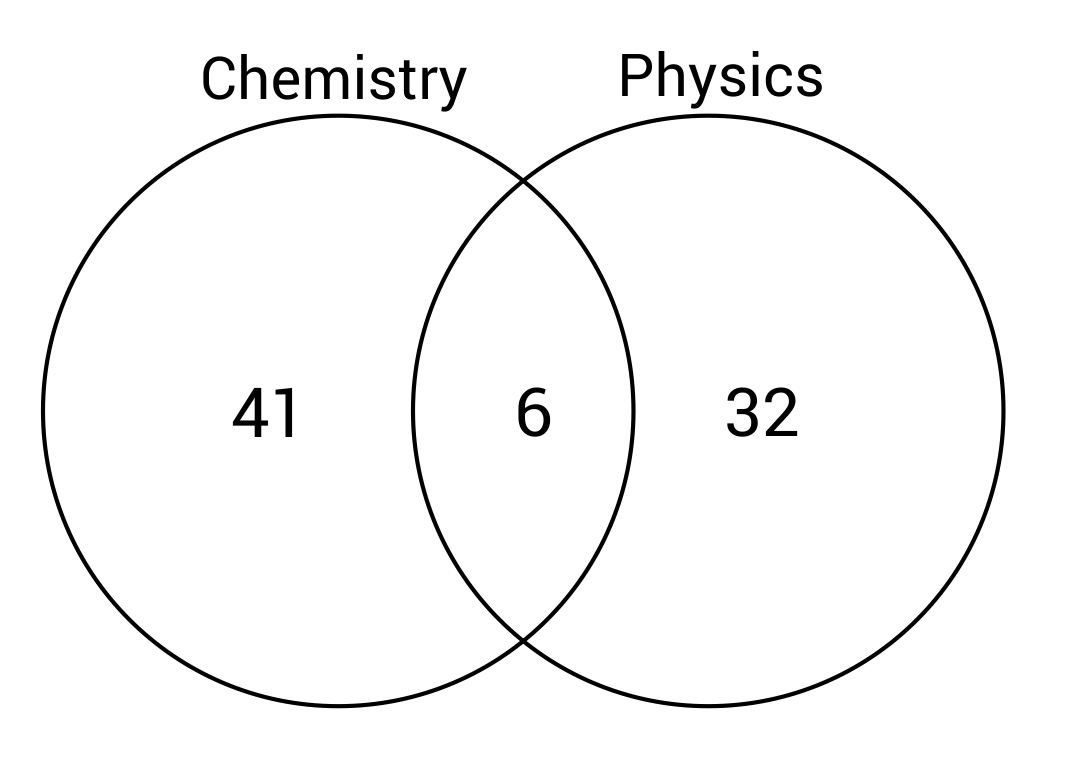
Forty-one students are enrolled in Chemistry exclusively, and thirty-two students are enrolled in Physics exclusively. The difference can be calculated by subtracting thirty-two from forty-one.
\(41-32=9\)
The following Venn diagram shows the number of students enrolled in Chemistry, Physics, or both. Based on the information provided, what is the total number of students?

41 students are exclusively enrolled in Chemistry, and 32 students are exclusively enrolled in Physics. \(41+32=73\text{ students}\). 6 students are enrolled in both classes, so 6 should be added to 73. \(6+73=79\text{ total students}\).
According to the Venn diagram, which pets would not be kept indoors?
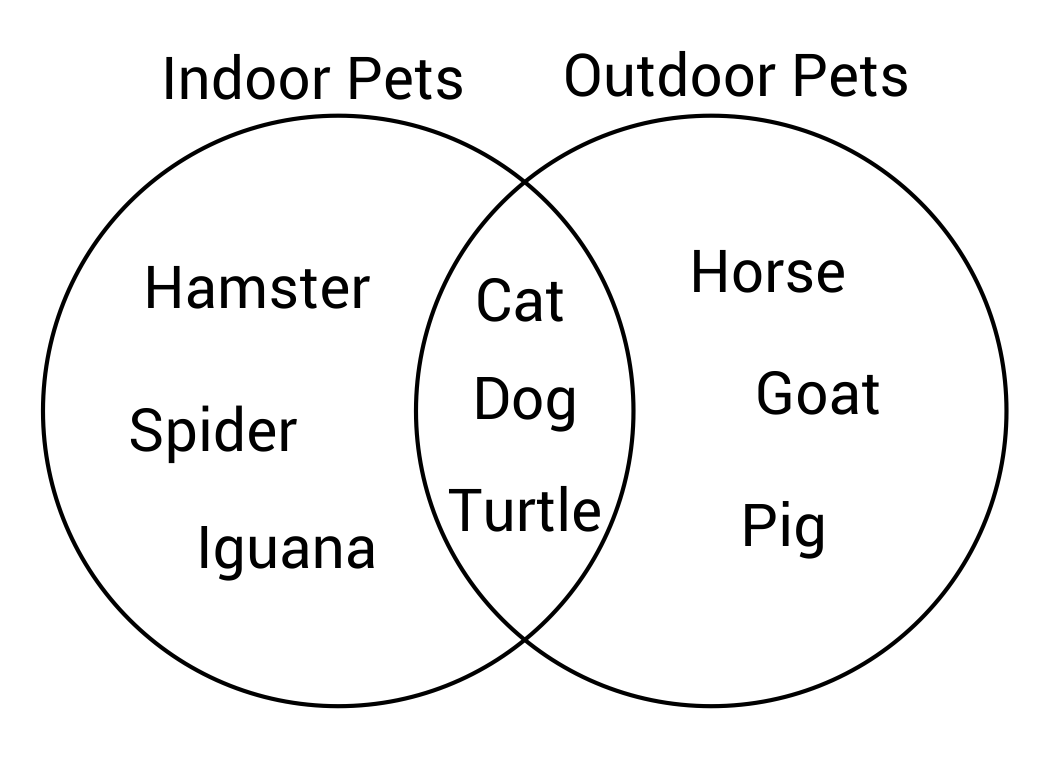
The pets that would not be kept indoors are listed on the far right portion of the Venn diagram. This portion lists horse, goat, and pig as being exclusively outdoor pets.
According to the Venn diagram, which pets are considered indoor and outdoor pets?

The overlapping middle portion of the Venn diagram shows animals that are considered both indoor and outdoor pets. The pets in this middle section are cats, dogs, and turtles.
Compare the number of factors of sixteen, to the number of factors of twenty-four. How many more factors does twenty-four have?
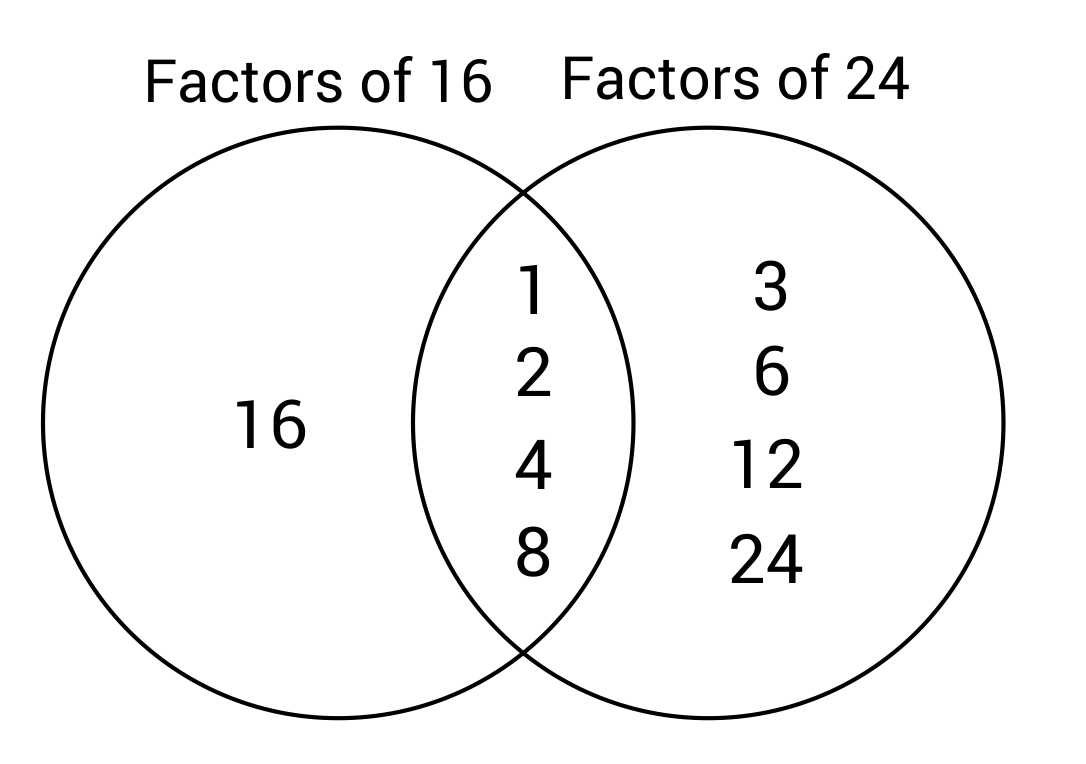
The number twenty-four has eight factors: 1, 2, 3, 4, 6, 8, 12, 24.
The number sixteen has five factors: 1, 2, 4, 8, 16.
Twenty-four has three more factors than sixteen.
According to the Venn diagram, how many factors are exclusive to twenty-four?

The factors that are exclusive to twenty-four are 3, 6, 12, and 24. The other factors of twenty-four (1, 2, 4, and 8) are shared with sixteen.
The Venn diagram below will display the factors of thirty, twenty, and twenty-six when filled out. Which factors will be listed in the section between 20 and 30, with no overlap with 26?
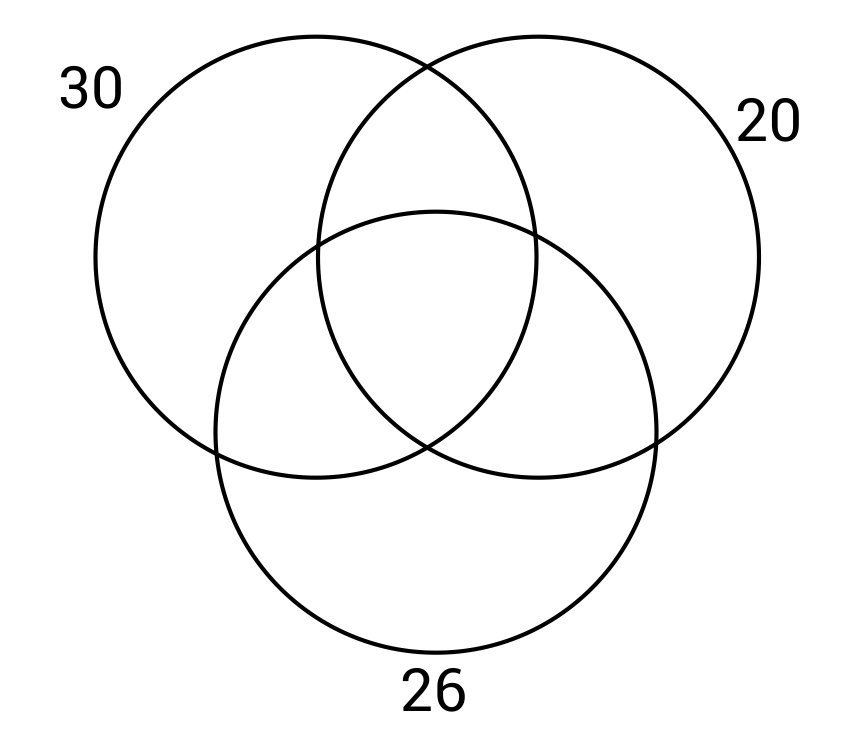
The factors of 20: 1, 2, 4, 5, 10, and 20.
The factors of 26: 1, 2, 13, and 26.
The factors of 30: 1, 2, 3, 5, 6, 10, 15, and 30.
The factors that 20 and 30 have in common are 1, 2, 5, and 10. However, 1 and 2 are also shared with 26, so these will not be in the section shared only by 20 and 30. The only factors shared by 20 and 30 but not 26 will be 5 and 10.
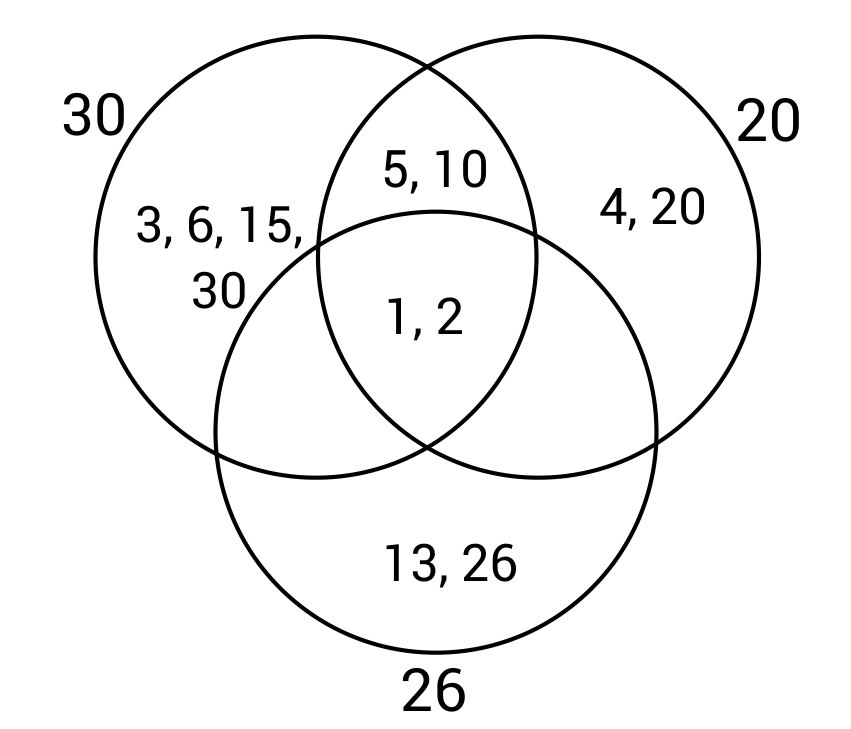
Which factors are exclusive to the number thirty? Which section of the Venn diagram will these factors be placed?
The top left section of the Venn diagram is for factors that are exclusive to thirty. The factors 3, 6, and 15 are not factors of twenty or twenty-six, so they will not be contained in any overlapping region.

If each sport requires a separate jersey, how many jerseys will need to be ordered so that the students can play all of the sports they are registered for?
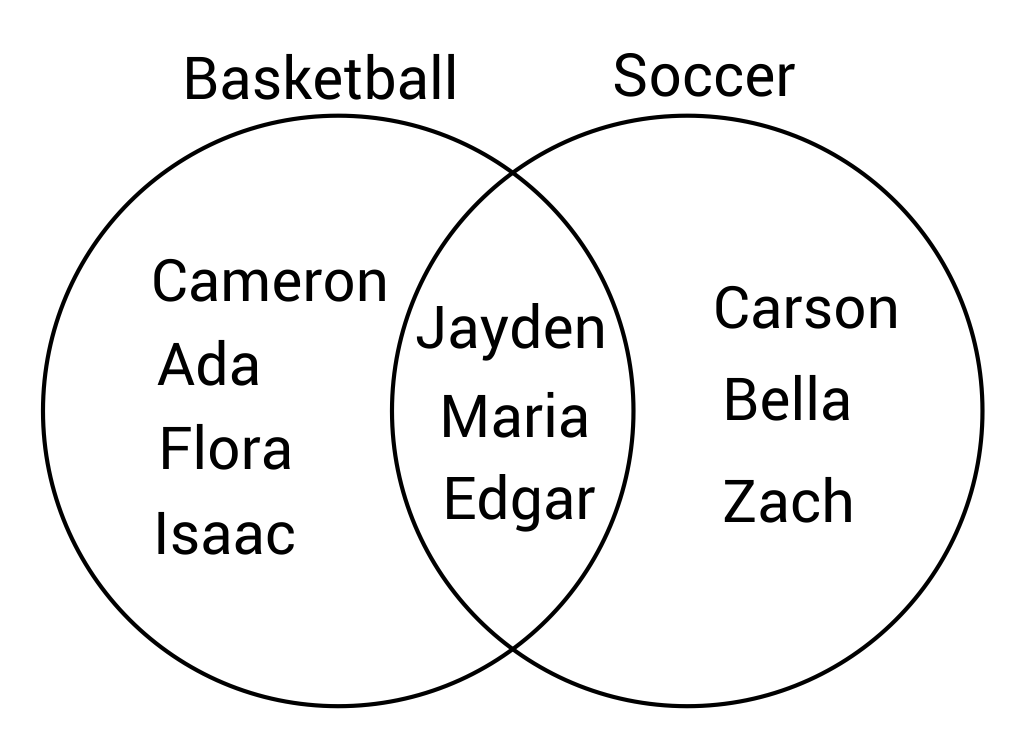
There 7 students registered for basketball, and 6 students registered for soccer. This means that a total of 13 jerseys need to be ordered for the students.
How many more students are registered for basketball than soccer?

There are 7 students registered for basketball, and 6 students registered for soccer. This means that basketball has one more student than soccer.
