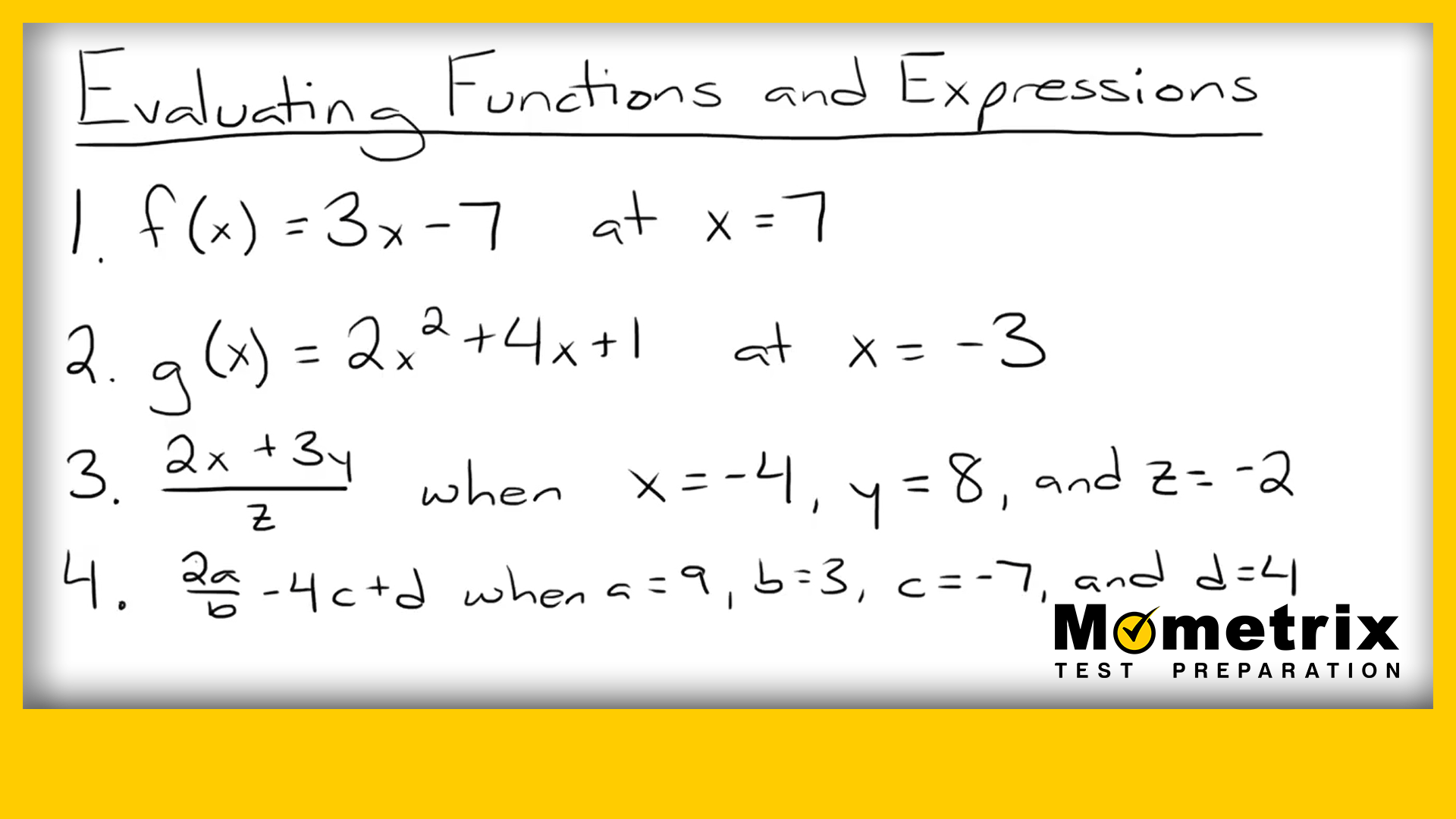Evaluating Functions
Hello! Today we are going to take a look at evaluating functions and expressions. All this requires is plugging in different values for variables and simplifying. Let’s start with a super simple example.
Evaluate the function \(f(x)=3x-7 \text{ at } x=6\).
To solve, start by plugging in 6 anywhere you see an \(x\).
\(f(6)=3(6)-7\)
Using parentheses helps you keep the operations straight; we know that we need to multiply 3 and 6.
Now, we were asked to evaluate the function at \(x=6\). When written in function notation like this, all we need to do is solve for \(f(6)\). So we just need to simplify the right side of the equation. Start by multiplying 3 and 6.
\(f(6)=18-7\)
Now, subtract.
\(f(6)=11\)
Let’s try another one.
Evaluate the function \(g(x)=2x^{2}+4x+1\) at \(x=-3\).
Don’t let the \(g(x)\) confuse you! Treat it just like you would if it were an \(f(x)\). Since we are evaluating at \(x=-3\), solve for \(g(-3)\).
Start by plugging in \(-3\) anywhere you see an \(x\).
\(g(-3)=2(-3)^{2}+4(-3)+1\)
Notice how important our parentheses are in our first term: \(2(-3)^{2}\). If we didn’t have them, it would look like this: \(2-3^{2}\). You would mistakenly subtract a positive number squared instead of multiplying by a negative number squared. So the parentheses are really important to keep our numbers straight.
Now that we’ve properly plugged in our value for \(x\), let’s simplify the expression by following the order of operations. First, simplify the exponents.
\(g(-3)=2(9)+4(-3)+1\)
Then, multiply.
\(g(-3)=18-12+1\)
And finally, add and subtract.
\(g(-3)=7\)
We’ve taken a look at evaluating functions. Now let’s take a look at evaluating expressions. In questions like these, we will follow the same steps we have been. The only difference is there will be more variables. Let’s try a problem.
Simplify the expression \(\frac{2x+3y}{z}\) when \(x=-4\), \(y=8\), and \(z=-2\).
First, plug in the given values for \(x\), \(y\), and \(z\). Make sure to use parentheses!
\(\frac{2(-4)+3(8)}{(-2)}\)
Now, simplify the expression. We will start by simplifying the numerator. First, multiply.
\(\frac{-8+24}{-2}\)
It’s okay that we dropped the parentheses in the denominator because -2 is the only term. Now, add -8 and 24.
\(\frac{16}{-2}\)
Remember, a fraction bar means division, so divide \(16\div (-2)=-8\).
Not too hard. Let’s try one last example together.
Simplify the expression \(\frac{2a}{b}-4c+d\) when \(a=9\), \(b=3\), \(c=-7\), and \(d=4\).
Start by substituting in the numbers.
\(\frac{2(9)}{3}-4(-7)+(4)\)
Now, simplify the expression. We’re going to start by multiplying.
\(\frac{18}{3}+28+4\)
Now we’re going to divide.
\(6+28+4\)
Finally, add these three numbers to get 38, which is your final answer.
I hope this video helped you better understand how to evaluate functions and expressions. Thanks for watching and happy studying!
Evaluating Function Practice Questions
Evaluate \(f\left(x\right)=4x^2-5x+6\) at \(x=3\).
27
15
3
10
Since we are evaluating the function at \(x=3\), we need to find \(f(3)\). Start by substituting 3 into the function anywhere you see an \(x\).
\(f\left(3\right)=4{(3)}^2-5(3)+6\)
Follow the order of operations to simplify the right side.
\(f\left(3\right)=4\left(9\right)-5\left(3\right)+6\)
\(=36-15+6\)
\(=21+6\)
\(=27\)
So, \(f\left(3\right)=27\).
Evaluate \(g\left(x\right)={-x}^2-5x+8\) at \(x=-4\).
44
20
12
4
Since we are evaluating the function at \(x=-4\), we need to find \(g(-4)\). Start by substituting –4 into the function anywhere you see an \(x\).
\(g\left(-4\right)={-(-4)}^2-5(-4)+8\)
Follow the order of operations to simplify the right side.
\(g\left(-4\right)={-\left(-4\right)}^2-5\left(-4\right)+8\)
\(=-\left(16\right)-\left(-20\right)+8\)
\(=-16+20+8\)
\(=4+8\)
\(=12\)
So, \(g\left(-4\right)=12\).
Evaluate the expression \(\frac{p+2q}{r}+3p-2q\) when \(p=-6\), \(q=-3\), and \(r=4\).
33
-27
15
-15
First, substitute \(p=-6\), \(q=-3\), and \(r=4\) into the expression.
\(\frac{-6+2(-3)}{4}+3\left(-6\right)-2(-3)\)
Now, simplify the expression.
\(\frac{-6+\left(-6\right)}{4}+\left(-18\right)-2\left(-3\right)\)
\(=\frac{-12}{4}-18+6\)
\(=-3-18+6\)
\(=-21+6\)
\(=-15\)
Let the length of a rectangle be represented by the expression \(2x+1\) meters, and the width by the expression \(x+3\) meters. The area, \(A\), of the rectangle can be represented by the function \(A\left(x\right)=2x^2+7x+3\) square meters. If the width of the rectangle is 8 meters, what is its area in square meters?
\(120\text{ m}^2\)
\(152\text{ m}^2\)
\(88\text{ m}^2\)
\(58\text{ m}^2\)
The width of the rectangle is represented by the expression \(x+3\) meters and it is given that the width is 8 meters. Set \(x+3\) equal to 8 to find the value of \(x\).
\(x+3=8\)
\(x+3-3=8-3\)
\(x=5\)
To find the area of the rectangle, we can evaluate the given function at \(x=5\). To find \(A(5)\), substitute 5 into the area function anywhere you see an \(x\).
\(A\left(5\right)=2{(5)}^2+7(5)+3\)
Follow the order of operations to simplify the right side.
\(A\left(5\right)=2{(5)}^2+7(5)+3\)
\(=2\left(25\right)+(35)+3\)
\(=50+35+3\)
\(=85+3\)
\(=88\)
So, \(A\left(5\right)=88\), meaning the area of the rectangle is 88 square units.
A high school’s booster club sells hamburgers and hot dogs at a school football game to raise money for the football team. Each hamburger sells for $3, and each hotdog sells for $2. The profit generated by selling \(m\) hamburgers and \(n\) hot dogs can be represented by the expression, \(3m+2n-\frac{m+3n}{2}\). If 30 hamburgers and 20 hot dogs were sold at the football game, what was the profit the booster club generated, in dollars?
85
100
45
65
Since 30 hamburgers were sold at the football game, \(m=30\). Twenty hot dogs were sold, so \(n=20\).
To find the profit, first substitute \(m=30\) and \(n=20\) into the expression for profit.
\(3(30)+2(20)-\frac{(30)+3(20)}{2}\)
Now, simplify the expression.
\(90+40-\frac{30+60}{2}\)
\(=90+40-\frac{90}{2}\)
\(=90+40-45\)
\(=130-45\)
\(=85\)
The booster club generated a profit of $85 from the sales of hamburgers and hot dogs at the football game.
