Work (According to Physics)

Hi, and welcome to this video on work! In this video, we will discuss the concept of work in terms of physics and look at some different examples. Let’s get started!

Before learning about work in a physics context, it may be useful to try and get rid of any preconceived notions about the term. In physics, work has a more precise definition than in everyday usage. It is defined as the energy transferred when a force displaces an object. For example, when you push an object and it moves some distance, your hand has applied a force and did work on that object. The equation for mechanical work, where the force is in the same direction as the displacement of the object is work equals F times d,

\(W=Fd\)
 
where F is the applied force and d is the distance the object has moved. Work is measured in units of joules, like energy. It is obvious from this equation that you can have a force acting on the object without doing any work if the object doesn’t actually move. In this case, d = 0, so W = 0.

In many cases, there is more than one force acting on an object. Let’s go back to the example where your hand is pushing an object. Let’s say that the object is a box sitting on a table. While you push the box forward, friction, another force, is pushing the box in the opposite direction. In this case, the force is negative since it points in the direction opposing the box’s motion. This means that friction is doing negative work on the box and the value for work of friction will be negative, while the work done by your hand is positive. Essentially, negative work makes it more difficult to keep an object moving in the positive direction.

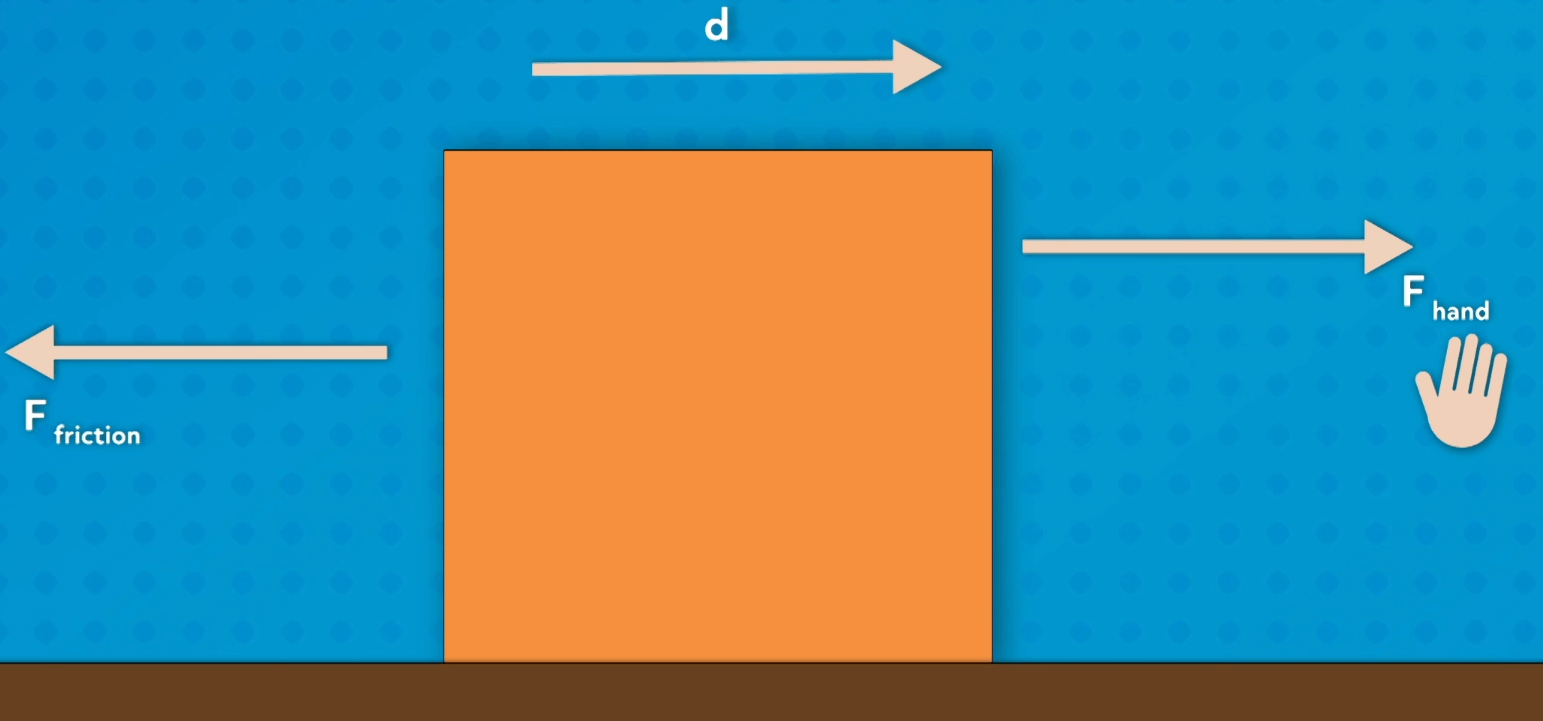
It’s also important to note that the total or net work done on an object is equal to the net force times the displacement. So, in our example, there are two forces and both must be accounted for to get the net work. The net work is the sum of the work done by your hand and the work done by friction. Remember, the work done by friction is negative because it is opposite of the direction of the object’s motion.

\(W_{net}=W_{hand}-W_{friction}=(F_{hand}\times d)-( F_{friction}\times d)\)
 
Since both forces act over the same distance, the d can be factored out. The sum of the forces is also called the net force. Thus, the net work equals the net force times the displacement.

\(W_{net}=(F_{hand}-F_{friction})\times d=F_{net}d\)
 
Sometimes the force applied to an object is not in a direction parallel to the motion of the object at all. While work is a scalar quantity, the force and displacement of an object are vectors, which means they always have a magnitude and a direction. Only the force component that’s in the direction of motion will contribute to the work. The equation W = F times d is actually a special case, and the more general form of the equation for work is: Work equals the magnitude of force times the magnitude of displacement times cosine of theta,

\(W=|F||d|cos θ\)
 
where theta is the angle between the force and displacement vectors. When the force and displacement are in the same direction, theta = 0° and cosine of theta = 1, leaving us with the familiar W = F times d. When the force and displacement are in opposite directions, as in the case of negative work, theta = 180°, and cosine of theta = – 1.

Let’s consider an example where the force and displacement are not at a 0° or 180° angle. Imagine someone dragging a heavy box along a frictionless surface by a rope. The person pulls the rope at an angle of 30° from the horizontal with a force of 52 Newtons and the box is moving along with the person. However, there is another rope attached to the other side of the box and a playful dog comes along and pulls in the opposite direction. The dog is about the same height as the spot the rope is attached to and pulls directly opposite the direction of motion with a force of 28 Newtons. The person pulls the box another 2 meters before they notice the dog and stop.

So, how do we go about finding the net work in this scenario?

First, let’s find the work that the person has done over the 2 meters. If we multiply the Newtons times the meters, then multiply that times the cosine of 30°, we get 90.1 joules.

\(W_{person}=(52N)(2m)cos(30°)=90.1\text{ J}\)
 
Now let’s figure out the negative work from the dog. We can use the full work equation with θ = 180°, or we can note that the force is in the opposite direction as the motion of the box and say that F = -28 Newtons. Either way, we will get the same answer. So, let’s stick with our work equation: 28 Newtons times 2 meters times the cosine of 180° equals -56 joules.

\(W_{dog}=(28N)(2m)cos(180°)=-56\text{ J}\)
 
Then, we just need to add these together to get the total work done in this system.

\(90.1\text{ J }+(-56\text{ J})=34.1\text{ J}\)
 
And that’s it! The net work here is 34.1 joules.

By now you should have a good idea of what mechanical work is and how to calculate it, so let’s test your knowledge with a couple of questions!

How much work do you need to put in to lift a 2kg ball 1 meter from the ground?

1. 2 joules
2. 0 joules
3. 19.6 joules
4. -19.6 joules

The correct answer is C, 19.6 joules. You will need to exert a force of 2kg times 9.8 meters per second squared, which is 19.6 Newtons to lift up the ball.

\(mg=(2kg)(9.8 m/s^2)=19.6\text{ N}\)
 
The work required to lift it by 1 meter is 19.6 Newtons times 1 meter, which equals 19.6 joules.

\((19.6 N)(1m)=19.6\text{ J}\)
 
The work is positive because you are exerting an upward force in the same direction of motion.

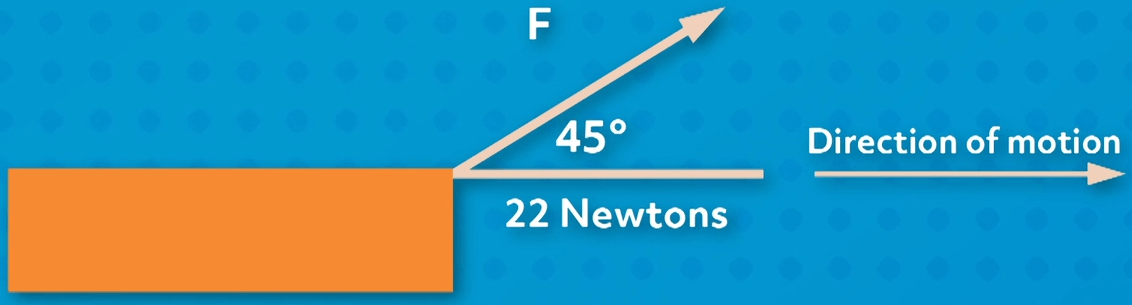
A child pulls a wagon with the handle at an angle of 45° with a force of 22 Newtons. How far can the child pull the wagon if they put in exactly 30 joules of work (assuming there is no friction)?

1. 1.9 meters
2. 15.6 meters
3. 4 meters
4. 1.4 meters

Plugging in these values into our equation, we get

\(30\text{ J}=(22N)\text{d cos}(45°)\)
 
Solving for d, we get d = 1.9 meters.

I hope this review was helpful! Thanks for watching, and happy studying!