Sum and Difference Trigonometric Identities
Hi, and welcome to this review of the sum and difference trigonometric identities! We have a lot of useful formulas to cover in this video, so let’s get started!
Before we dive in, let’s take a moment to review the unit circle. The unit circle gives you the sine and cosine values for some of the most common angle measures.
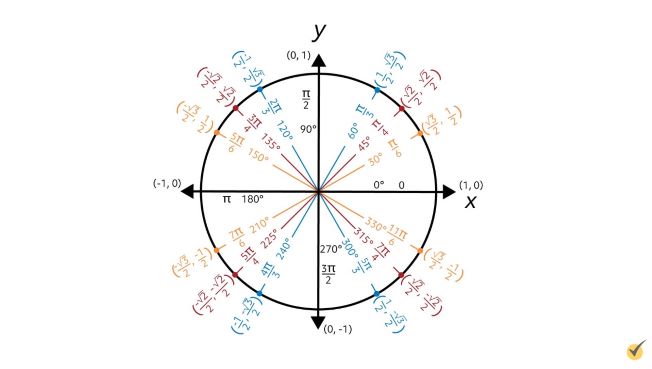
With this information, combined with some of the formulas we’re going to cover today, we can find the exact trigonometric values of even more angles on the unit circle, all without using a calculator.
Let’s start with the sum identities. The first one we’ll use is the formula for finding the sine of the sum of two angles. Let’s look at the formula:
\(sin(a+\beta )=sin\text{ }\alpha \text{ }cos\text{ }\beta + cos\text{ }\alpha \text{ }sin\text{ }\beta\)
So if we want to find the sine of 75 degrees, we can do this by finding two angles that add up to 75 and using them as \(\alpha\) and \(\beta\). Fortunately, that’s easy to find on our unit circle. Since \(30+45=75\), we can use 30 as \(\alpha\) and 45 as \(\beta\). We could also use 45 as \(\alpha\) and 30 as \(\beta\). It doesn’t really matter.
First, let’s write down the information we need for our two angles. We’re using 30 degrees as \(\alpha\), so we’re going to write down, \(\alpha\)=30°, and then we’ll look up our cosine and our sine values from our unit circle.
\(\alpha=30°\)
\(cos(30°)=\frac{\sqrt{3}}{2}\)
\(sin(30°)=\frac{1}{2}\)
Then we do the same thing for \(\beta\), which we’ve set as 45 degrees.
\(\beta=45°\)
\(cos(45°)=\frac{\sqrt{2}}{2}\)
\(sin(45°)=\frac{\sqrt{2}}{2}\)
Now, we’ll write down our formula for the sine sum identity.
\(sin(\alpha +\beta)=sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta)\)
Then we’ll substitute 30 degrees for \(\alpha\), 45 degrees for \(\beta\), and then substitute all of our sine and cosine values into the right side of our formula.
\(sin(30°+45°)=sin(30°)cos(45°)+cos(30°)sin(45°)\)
Then we’re going to substitute in our sine and cosine values.
\(sin(75°)=(\frac{1}{2})(\frac{\sqrt{2}}{2})+(\frac{\sqrt{3}}{2})(\frac{\sqrt{2}}{2})\)
Now we’re going to simplify with a little bit of multiplication.
\(sin(75°)=\frac{\sqrt{2}}{4}+\frac{\sqrt{6}}{4}\)
Finally, because both terms have the same denominator, we can write our answer as a single fraction.
\(sin(75°)=\frac{2+\sqrt{6}}{4}\)
As you can see, it’s important to be strong in handling radicals and fractions to do this kind of work. We can check our answer by using a calculator. If we add the \(\sqrt{2}\) to the \(\sqrt{6}\) and then divide by 4, we get approximately 0.966.
\(sin(75°)=\frac{\sqrt{2}+\sqrt{6}}{4}\approx 0.966\)
If we then use a calculator to find the sine of 75°, we get the same thing.
But that begs the question, “Why don’t we just use a calculator to find the sine instead of doing all this work?” The answer is that the calculator is giving us an approximate value of the sine of 75 degrees. If we want to know the exact value, we need to do it the long way. When taking a standardized test, if you see the word “exact” in reference to a problem like this, then you’ll know how to do this process.
What if we want to find the exact value of the cosine of 75 degrees? We have a sum identity formula for that too:
\(cos(\alpha+\beta)=cos(\alpha) cos(\beta)-sin (\alpha) sin (\beta)\)
It works in a similar way. We can plug in our values and find the cosine pretty quickly.
We start by writing down our cosine sum identity. It’s really easy to mix up the values if you don’t do this, so it’s always a good idea.
\(cos(\alpha+\beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)\)
Then, we’ll substitute 30 degrees for \(\alpha\), 45 degrees for \(\beta\), and then substitute all of our sine and cosine values into the right side of the formula just like we did with the last problem.
\(cos(30°+45°)=cos(30°)cos(45°)-sin(30°)sin(45°)\)
Then we’ll plug in our sine and cosine values. So, first we’ll simply this left side.
\(cos(75°)=(\frac{\sqrt{3}}{2})(\frac{\sqrt{2}}{2})-(\frac{1}{2})(\frac{\sqrt{2}}{2})\)
Once again we do some multiplication and write our answer as a single fraction.
\(cos(75°)=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4}\)
Just like the last problem, we can check our work by evaluating this radical expression on a calculator and then finding the approximate value of the cosine of 75° on the calculator.
\(\frac{\sqrt{6}-\sqrt{2}}{4}=0.25881904510252\)
\(cos(75°)=0.25881904510252\)
It matches up, so we did something right!
There’s also a sum identity for tangent:
\(tan(\alpha + \beta)=\frac{tan\text{ }\alpha + tan\text{ }\beta}{1-tan\text{ }\alpha\text{ }tan\text{ }\beta}\)
Let’s use this identity to answer this question:
What is the exact value of the tangent of 75 degrees?
In order to figure this out, we need to find the tangent of 30 degrees and the tangent of 45 degrees. But that information isn’t on our unit circle. Fortunately, we can find it easily enough because we know that:
\(tan(\alpha)=\frac{sin\text{ }\alpha}{cos\text{ }\beta}\)
We could do that twice for each of the two angles we need and then plug it into the sum identity for tangent, but since we just found the exact value for the sine and cosine of 75 degrees by using the sum identities for both sine and cosine, we can plug those answers directly into this simpler identity to find our answer:
\(sin(75°)=\frac{\sqrt{2}+\sqrt{6}}{4}\)
\(cos(75°)=\frac{\sqrt{6}-\sqrt{2}}{4}\)
Now we’re going to write out our tangent identity.
\(tan(\alpha)=\frac{sin(\alpha)}{cos(\alpha)}\)
So if we want to know the \(tan(75°)\), we simply plug in the \(sin(75°)\) and then divide it by the \(cos(75°)\).
\(tan(75°)=\frac{sin(75°)}{cos(75°)}=\frac{\frac{\sqrt{2}+\sqrt{6}}{4}}{\frac{\sqrt{6}-\sqrt{2}}{4}}\)
Now, to simplify this, we can rewrite this as division of fractions.
\(\frac{\frac{\sqrt{2}+\sqrt{6}}{4}}{\frac{\sqrt{6}-\sqrt{2}}{4}}=\frac{\sqrt{2}+\sqrt{6}}{4}\div \frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\sqrt{2}+\sqrt{6}}{4} \frac{4}{\sqrt{6}-\sqrt{2}}=\frac{\sqrt{2}+\sqrt{6}}{\sqrt{6}-\sqrt{2}}\)
Now remember, when we divide fractions, we flip the second fraction and multiply them.
\(\frac{\sqrt{2}+\sqrt{6}}{4}\div \frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\sqrt{2}+\sqrt{6}}{4}\cdot \frac{4}{\sqrt{6}-\sqrt{2}}\)
Now we can multiply these together.
\(\frac{\sqrt{2}+\sqrt{6}}{4} \cdot \frac{4}{\sqrt{6}-\sqrt{2}}=\frac{\sqrt{2}+\sqrt{6}}{\sqrt{6}-\sqrt{2}}\)
If we didn’t know the sine and cosine of 75 degrees, it would make sense to use our sum identity for tangent. So let’s walk through what that would look like.
As usual, we start by writing down all the information we’re going to need. In this case, we have to use the fact that \(tan=\frac{sin}{cos}\) to find our values for the tangent of 30 and 45 degrees.
\(tan(30°)=\frac{sin(30°)}{cos (30°)}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\)
This comes from rationalizing the denominator which is something we’ll cover a little bit more later on in this video.
\(tan(45°)=\frac{sin(45°)}{cos(45°)}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=1\)
Next, we write out our tangent sum identity.
\(tan(\alpha+\beta)=\frac{tan(tan(\alpha)+tan(\beta)}{1-tan(\alpha)tan(\beta)}\)
Then, we’ll substitute 30 degrees for \(\alpha\), 45 degrees for \(\beta\), and then substitute all of our tangent values into our formula.
\(tan(30°+45°)=\frac{tan(30°)+tan(45°)}{1-tan(30°)tan(45°)}\)
Now, let’s plug in our tangent values.
\(tan(30+45)=\frac{\frac{\sqrt{3}}{3}+1}{1-(\frac{\sqrt{3}}{3})(1)}=\frac{\frac{\sqrt{3}}{3}+\frac{3}{3}}{1-\frac{\sqrt{3}}{3}}=\frac{\frac{\sqrt{3}+3}{3}}{\frac{3-\sqrt{3}}{3}}= \frac{\sqrt{3}+3}{3}\div \frac{3-\sqrt{3}}{3}=\frac{\sqrt{3}+3}{3}\cdot \frac{3}{3-\sqrt{3}}=\frac{\sqrt{3}+3}{3-\sqrt{3}}\)
Notice that the two answers for our two different methods don’t appear to be the same. But if we enter them into a calculator, we’ll get the same value:
\(\frac{\sqrt{3}+3}{3-\sqrt{3}}=3.7320508075\)
\(\frac{\sqrt{2}+\sqrt{6}}{\sqrt{6}-\sqrt{2}}=3.7320508075\)
This is the same value we get when we ask the calculator for the tan of 75 degrees too!
\(tan(75°)=3.7320508075\)
The reason the answers look different from each other is that they haven’t been fully simplified. If you’ll notice, there’s a radical in the denominator. To fix both answers, we need to multiply the top and bottom of our answers by the conjugate of the denominator, which looks just like the denominator but has the opposite sign between the two terms. Then we can simplify even further and see if we can make the answers look the same.
Let’s start with the first one. First, we need to make a conjugate version of the denominator and multiply the answer. The conjugate means that the sign in between the two terms is going to change.
\(\frac{\sqrt{2}+\sqrt{6}}{\sqrt{6}-\sqrt{2}}\cdot \frac{\sqrt{6}+\sqrt{2}}{\sqrt{6}+\sqrt{2}}\)
This fraction simplifies to 1, so we’re not changing the value of our fraction at all. Now we can use FOIL to multiply our numerators and denominators together.
\(\frac{\sqrt{12}+\sqrt{4}+\sqrt{36}+\sqrt{12}}{\sqrt{36}+\sqrt{12}+(-\sqrt{12})+(-\sqrt{4})}\)
Now we’ll simplify our radicals a little bit.
\(\frac{2\sqrt{3}+2+6+2\sqrt{3}}{6+2\sqrt{3}-2\sqrt{3}-2}\)
Now we can combine like terms in our numerator.
\(\frac{4\sqrt{3}+8}{4}\)
From here we can factor 4 out of our numerator.
\(\frac{4(\sqrt{3}+2)}4\)
Our 4s will cancel each other out and we’ll be left with \(\sqrt{3}+2\).
Okay, now I’ll do the same thing to the other one. Again, we’re going to multiply by fraction that has the conjugate in both the numerator and denominator. So the conjugate of \(3-\sqrt{3}\) is \(3+\sqrt{3}\).
\(\frac{\sqrt{3}+3}{3-\sqrt{3}}\cdot \frac{3+\sqrt{3}}{3+\sqrt{3}}\)
Then we’re going to FOIL our numerators and denominators, and simplify our roots.
\(\frac{3\sqrt{3}+\sqrt{9}+9+3\sqrt{3}}{9+3\sqrt{3}+(-3\sqrt{3})+(-\sqrt{9})}=\frac{3\sqrt{3}+3+9+3\sqrt{3}}{9-3}\)
Now we can combine like terms in our numerator and denominator, and factor a 6 out of the numerator to simplify.
\(\frac{6\sqrt{3}+12}{6}=\frac{6(\sqrt{3}+2)}{6}=2+\sqrt{3}\)
So we can see that both of our values are equal to the same thing, even though originally they looked a little bit different. And this is a much nicer number. So rationalizing the denominator can sometimes be really useful.
We also have identities to find the difference of two angles rather than the sum. These are the difference identities for sine, cosine, and tangent:
\(sin(\alpha-\beta)=sin (\alpha) cos (\beta)-cos (\alpha) sin (\beta)\)
\(cos(\alpha-\beta)=cos (\alpha) cos (\beta)+sin (\alpha) sin (\beta)\)
\(tan(\alpha-\beta)=\frac{tan (\alpha) – tan (\beta)}{1 + tan (\alpha) tan (\beta)}\)
We use these the same way we use the sum identities, but they enable us to find some smaller angles. For instance, we could use the sine difference identity to find the sine of 15 degrees, using 45 degrees as \(\alpha\) and 30 degrees as \(\beta\).
Once again, we start by gathering the information we need and defining our \(\alpha\) and \(\beta\) angles to keep things organized and minimize the risk of a mistake. So for this problem, we’re saying that \(\alpha=45°\). Since we’re looking for a smaller angle, our alpha has to be bigger than our beta. So \(\beta=30°\).
\(\alpha=45°~~~~~~~~\beta=30°\)
\(sin(45°)=\frac{\sqrt{2}}{2}~~~~~~~~sin(30°)=\frac{1}{2}\)
\(cos(45°)=\frac{\sqrt{2}}{2}~~~~~~~~cos(30°)=\frac{\sqrt{3}}{2}\)
Now we’re going to write out our sum difference identity.
\(sin(\alpha-\beta)=sin(\alpha)cos(\beta)-cos(\alpha)sin(\beta)\)
Then we simply substitute all of the appropriate values into the formula.
\(sin(45°-30°)=sin(45°)cos(30°)-cos(45°)sin(30°)\)
\(sin(75°)=(\frac{\sqrt{2}}{2})(\frac{\sqrt{3}}{2})-(\frac{\sqrt{2}}{2})(\frac{1}{2})\)
Now we can multiply and simplify a little bit.
\(sin(15°)=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4}\)
This time there is no radical in our denominator so we don’t have to rationalize it.
We can check this value on a calculator by finding \(sin(15°)\). This gives us an approximate value of 0.259.
Remember, our answer with radicals is the exact value for \(sin(15°)\).
The cosine and tangent difference identities work the same way. We simply plug in our values and enjoy working with radicals until we have our answer.
I hope that this video helped you better understand the sum and difference identities of trig functions. Thanks for watching, and happy studying!