
Hi, and welcome to this video about the resistance of electric currents!
You plug in your cellphone to charge. You hear the roar of the car engine as it starts. You turn on a flashlight when the power goes out. These are a few examples of electric circuits: they bring electricity from a power source to an item that converts that power into something else. These circuits are made up of a power source, wires, and other components like switches and resistors.
Think about the plumbing in a house: the pipes deliver water to places where you use the water, like your sink and shower. Similarly, electric circuits deliver electricity to items and places that can use that electricity, like a light bulb, refrigerator, or TV.
The Flow of Electrons
Circuits deliver electricity using the flow of electrons through wires, and this flow is called an electrical current. Just like the water pipes create a flow of water molecules making up the water current, the circuit creates a flow of electrons making up the electric current. Current is measured in amperes, which is a unit of measure that tells us how many electrons are flowing through a point in one second.
In order to cause the electric current to flow, a voltage is applied to the circuit. A voltage difference causes the electrons to flow, just like a change in water pressure causes the water to flow. We can also think of voltage like the pulsing of your heart to push blood through your body. Your heart pushes on your blood to create blood flow, just like voltage pushes on electrons to create current. Voltage is measured in volts, a unit of measure that tells us how good our power source is at pushing an electron.
Resistance
Just like water pipes have ways for the water flow to be slowed, electric circuits also have ways for electric current to be slowed. This is called resistance. Resistance is like the diameter of the water pipe: a larger diameter water pipe has less resistance than a small diameter water pipe. Every material has an electrical resistance, and it is measured in ohms.
We use the Greek letter omega (Ω) to represent an ohm. This unit of measure tells us how easy is it for our electric current to move through the material. The wires in an electrical circuit have resistance R. It is determined by the length of the wire L, the resistivity of the wire rho (⍴), and the diameter of the wire D through the equation R equals ⍴ times L divided by D. In most circuits, we want the wires delivering the current to have as small a resistance as possible so the current can flow easily.
The Role of Resistance in Incandescent Bulbs
However, high resistance can be useful in some situations! An incandescent bulb has a twisted piece of wire in it. When you flip the switch to turn on the light, the voltage pushes the current through the wire, which has a very high resistance, so it is difficult for the current to move through. The wire begins to heat up. Eventually, the wire is so hot, light is created! Lightbulbs show us one way electricity can be used to change one form of energy to another. We are changing electrical energy into light and heat energy.
Voltage V, current I, and resistance R are related through Ohm’s Law: \(V=IR\).
From this relationship, we see that increasing resistance while keeping the current the same means the voltage must increase. It’s like using your thumb to spray water from a hose: you have increased the resistance for the water to flow through the hose, so more pressure is needed to keep the same water current flowing.
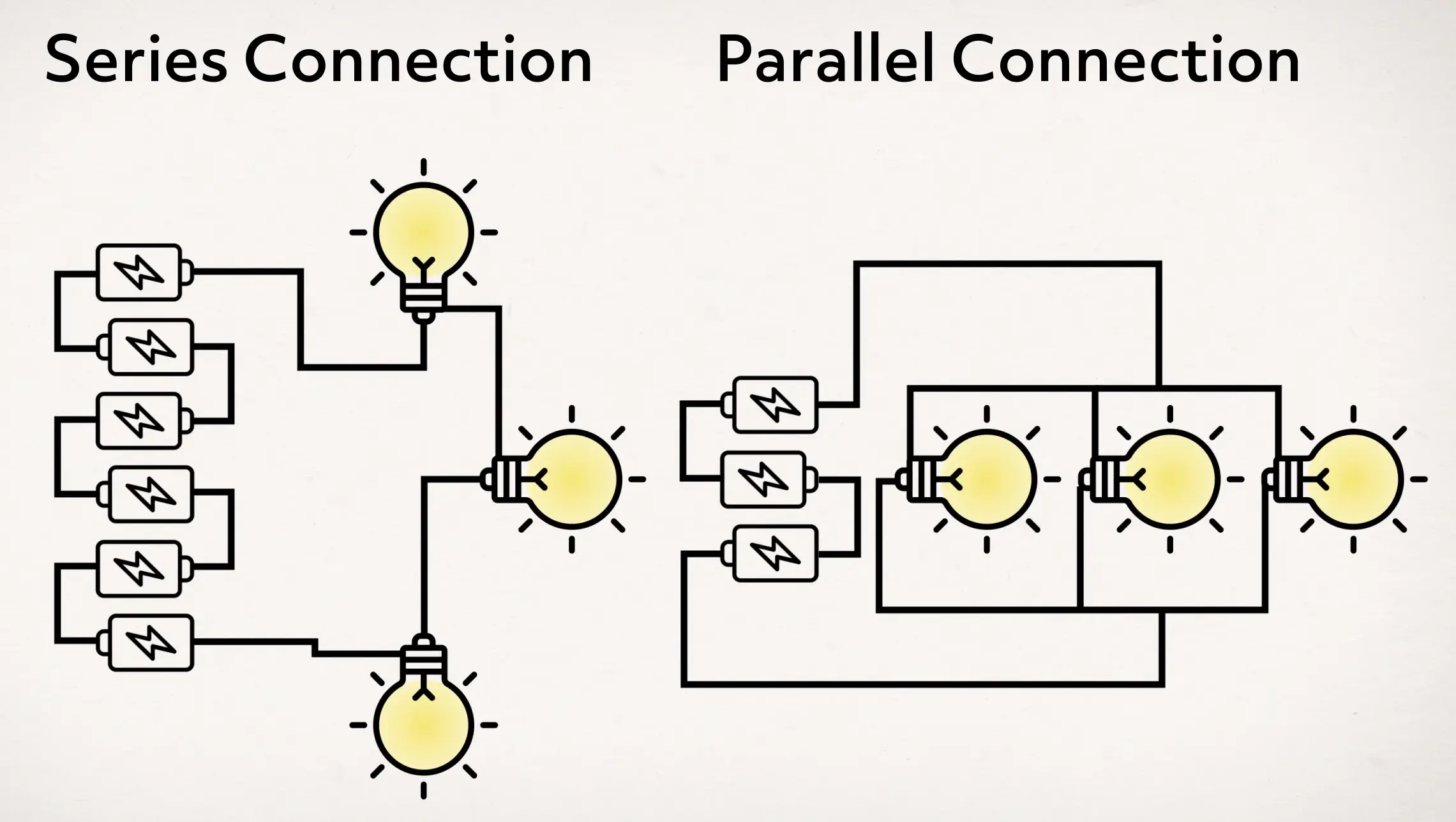
Resistors in Series
Resistors can be linked together in a long chain; this is called a series circuit. Linking resistors in this way means each resistor receives the exact same current. However, the voltage drops across each resistor are dependent on its resistance R. Suppose we have three resistors in a row: R1, R2, and R3. We would like to replace these three resistors with only one resistor that has the same resistance as the original series. This is called an equivalent resistance.
Since the current is the same in each resistor, the relationship is additive: R1 plus R2 plus R3 equals R equivalent. It’s like connecting two garden hoses together: the hoses are in series and it takes more water pressure to push the water through the hoses. Similarly, it takes more voltage to push the current through many resistors in series.
An example of resistors in series is a string of old Christmas lights. The light bulbs form a series of resistors: each bulb has a resistance. If one bulb burns out, the entire string of lights does not light up. This is because the current has been cut off. To make the lights work again, you need to find the broken bulb and replace it… which can take a while.
Resistors in Parallel
Newer strings of lights don’t have this problem because the resistors are in parallel. This means they each have the same voltage across them but different currents. If one bulb burns out, the rest of the bulbs still work because they still have current. The equivalent resistance of resistors in parallel is 1 divided by R equivalent equals 1 divided by R1 plus 1 divided by R2 plus 1 divided by R3. This relationship follows from Ohm’s law, which shows us how the current branches into the different resistors.
Review Question
Let’s wrap up with a review question!
I want to string together fifteen strings of Christmas lights. As I add more and more Christmas lights to my string, the lights get dimmer and dimmer! Why?
- I do not have enough Christmas spirit.
- Adding more lights adds more resistance.
- Adding more lights adds more voltage.
Thanks for watching, and happy studying!