The term quadrilateral stems from the word quad, meaning “four,” and lateral, meaning “side.” A quadrilateral is defined as a closed two-dimensional figure, with exactly four sides and four angles. As you would expect, there are many shapes that can be created using four sides and four angles. The six most common polygons that fall under the umbrella of “quadrilateral” are: parallelograms, trapezoids, rectangles, squares, kites, and rhombuses (rhombi). Let’s take a closer look at the similarities and differences between each category of quadrilateral.
Some quadrilaterals can be classified in more than one group. A flow chart can be a helpful visual aid when learning which shapes fall into more than one category.
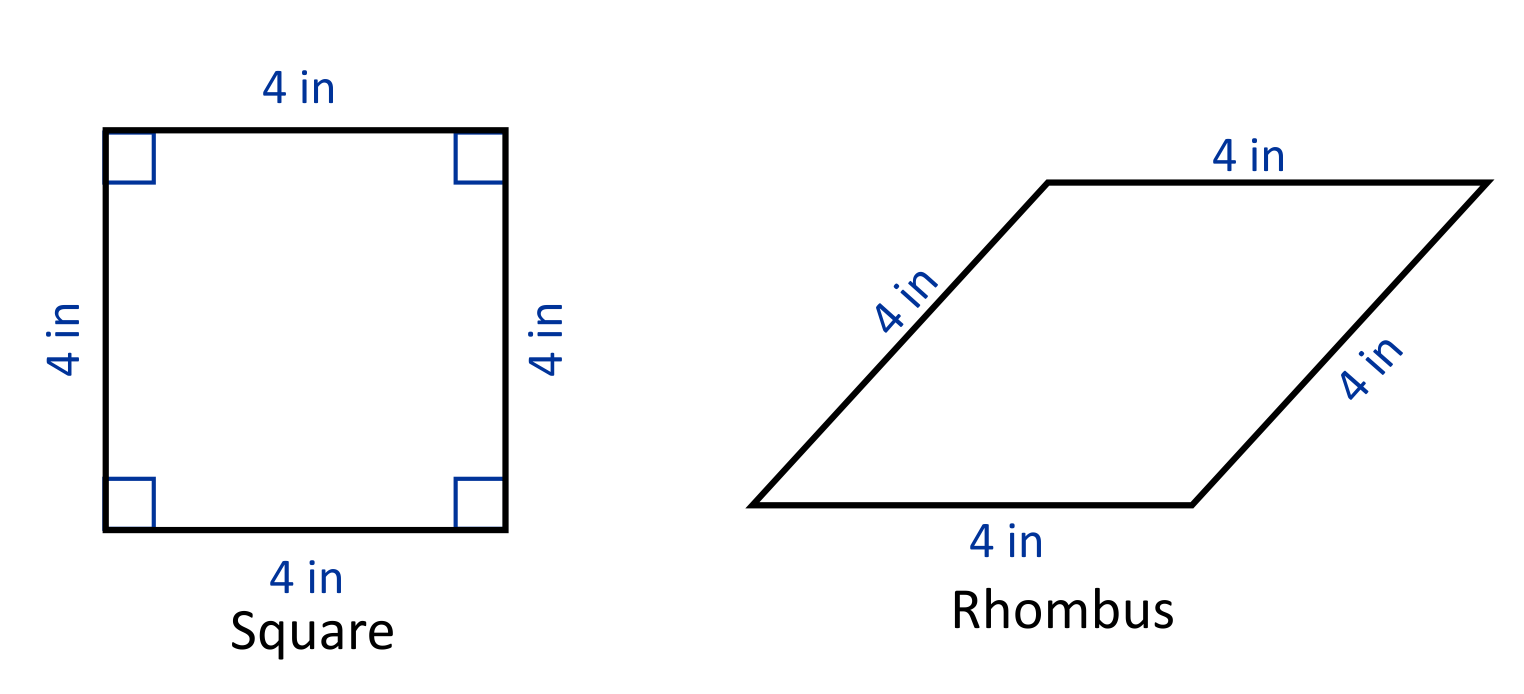
Let’s start in the category of “parallelogram”, with a shape that you are probably very familiar with: the square.
A square is a quadrilateral with four congruent side lengths, and four congruent angles. Similarly, a rectangle is a quadrilateral with four congruent angles, and opposite side lengths that are equal. This means that a rectangle can never be classified as a square, but technically a square can be classified as a rectangle. Similarly, a square can also be classified as a rhombus, but not all rhombuses will be classified as squares. This is because a rhombus has four congruent side lengths. However, the angle measures do not have to be congruent. Rectangles, rhombuses, and squares, all fall within the category of parallelograms because they all have two pairs of parallel sides.
A shape that is not considered a parallelogram is a trapezoid. A trapezoid has exactly one set of parallel sides. Within the trapezoid family, there are isosceles trapezoids. Isosceles trapezoids have congruent non-parallel sides.
The last shape that falls under the quadrilateral umbrella is the kite. A kite is a quadrilateral with no parallel sides.
As you can see, the term quadrilateral describes a wide range of polygons. These shapes are studied in great detail within the subject of geometry. Geometry is essentially the “study of shapes,” which has many useful real-world applications. For example, engineers use geometry to analyze the strengths and weaknesses of shapes when designing massive bridges. Bridges often utilize triangles because of their proven strength against weight and pressure. Geometry is also used in the field of astronomy. Shapes such as elliptical orbits are studied in order to determine the correct angle to enter a planet’s atmosphere safely. Geometry calculations were even used in the most recent Mars rover landing! As you can see, the field of geometry, and specifically the study of shapes, has many useful applications in the field of science, engineering, and math.
Quadrilateral Sample Questions
Here are a few sample questions going over quadrilaterals.
A quadrilateral is a ___ sided two-dimensional shape.
A quadrilateral is a two-dimensional shape, with four straight sides. Examples of quadrilaterals include parallelograms, trapezoids, rectangles, kites, squares, and rhombuses.
True or False: All squares are rhombuses, but not all rhombuses are squares.
A rhombus is a quadrilateral with four equal side lengths. This can take the form of a square, where all side lengths are equal, and all angles are 90°. However, shapes other than squares can be formed using four equal side lengths. Any shape with four equal side lengths is considered a rhombus. This is why a square is always a rhombus, but a rhombus is not always a square.
Aimee and Sam are building a bookshelf with a trapezoid as the base shape. They both draw a sketch of what they think the trapezoid should look like, but Aimee says that the shape Sam drew is not considered a trapezoid? Is she correct?
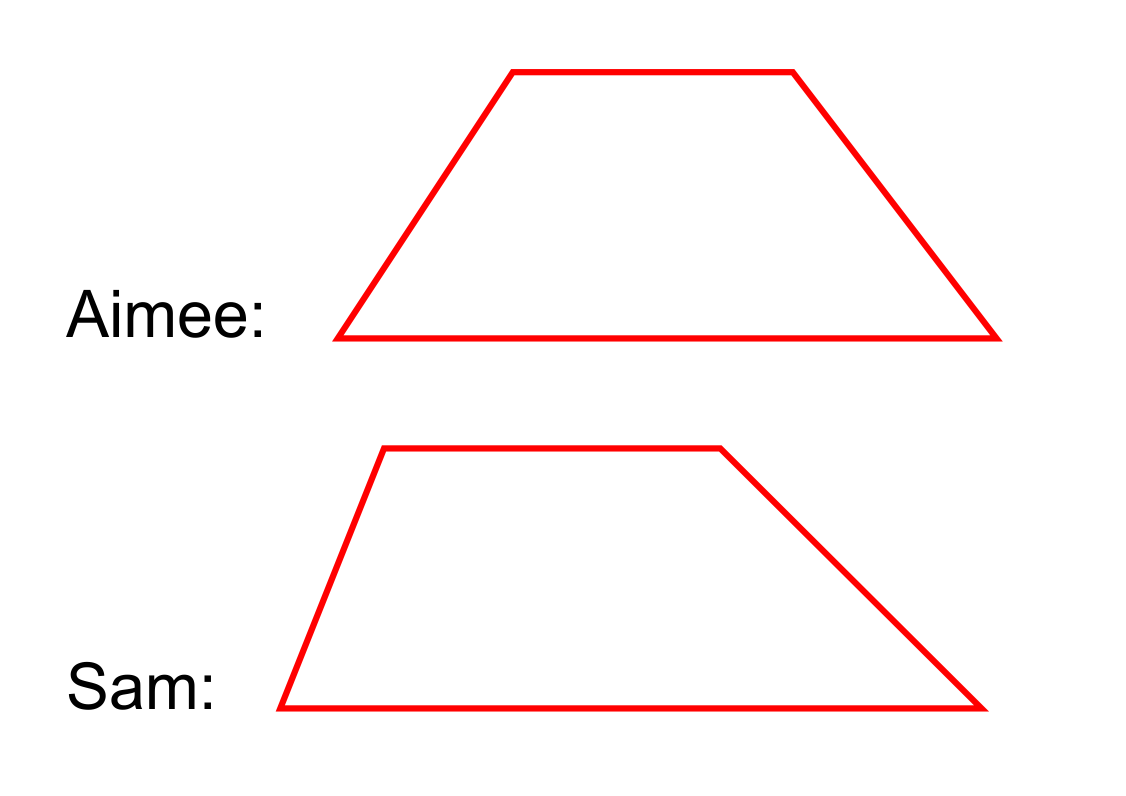
Aimee says that the shape Sam drew is not considered a trapezoid, which is incorrect. A trapezoid is defined as a quadrilateral with exactly one set of parallel sides. Aimee and Sam both drew quadrilaterals with exactly one set of parallel sides, so both shapes qualify as trapezoids.
How can the figure below be defined?
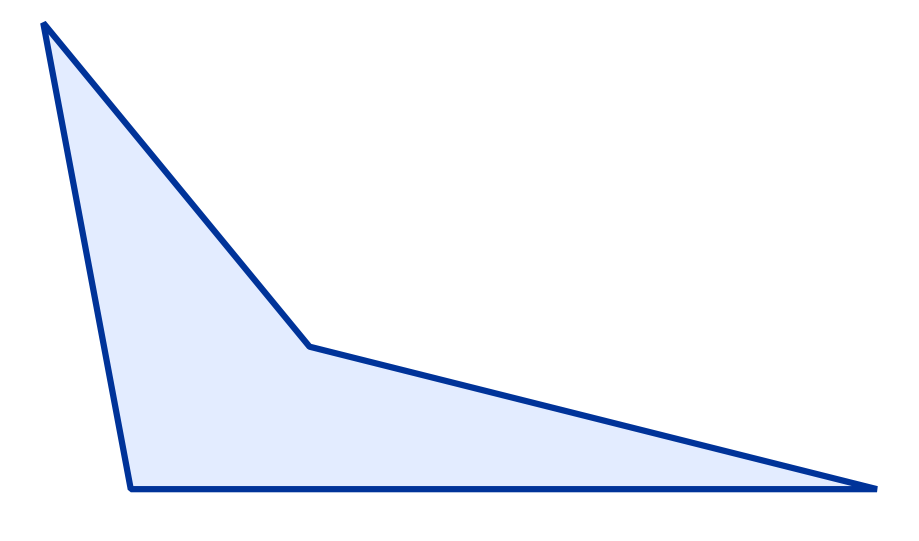
The figure is not a parallelogram because it does not have two sets of parallel sides. It is not a trapezoid because it does not have exactly one set of parallel sides. It is not a rhombus because it does not have four congruent side lengths. However, it is considered a quadrilateral because it is a closed shape with four sides and four angles.
Jenny is creating necklaces to sell at the farmers market. She creates the necklaces using small pieces of colorful stones. How should Jenny describe the flat face of the stones to her customers?

The flat face of the stones are four-sided, with exactly one set of parallel sides. This means that they can be classified as trapezoids.

