
Hi, and welcome to this video on calculating the percent yield of a chemical reaction!
It’s an important concept, particularly in the laboratory, and is often used as a method for measuring the success of a reaction. As this is a concept best learned through practice, we’ll start with a quick definition but then jump right into some examples.
Percent Yield: Actual vs. Theoretical
The simple definition of percent yield is the actual yield divided by the theoretical yield times 100 (to convert to a percentage).
The theoretical yield is the maximum amount of product a reaction could produce. The key word here is theoretical. In theory, if everything went perfectly and 100% of the reactants were converted to product, we would achieve our theoretical yield. However, mistakes happen or the reaction doesn’t finish or a competing reaction produces something else; in any case, we rarely obtain our theoretical yield. What we produce in the lab is the actual yield.
So, now that we have these basic definitions, let’s walk through an actual synthesis.
Example: Isopentyl Acetate
Say you’re going to make isopentyl acetate, commonly known as banana oil, in your organic chemistry lab.
You add together the two reactants, 7 mL of glacial acetic acid and 5 mL of isopentyl alcohol, along with a little sulfuric acid to catalyze the reaction. You mix it all up and heat the mixture. After a while, you decide it’s time to stop. You wash your banana oil with water to remove excess reactant, separate your product, and take its weight. And ta-da! 4.6 grams of product. This is your actual yield – the literal amount of product you made in the lab.
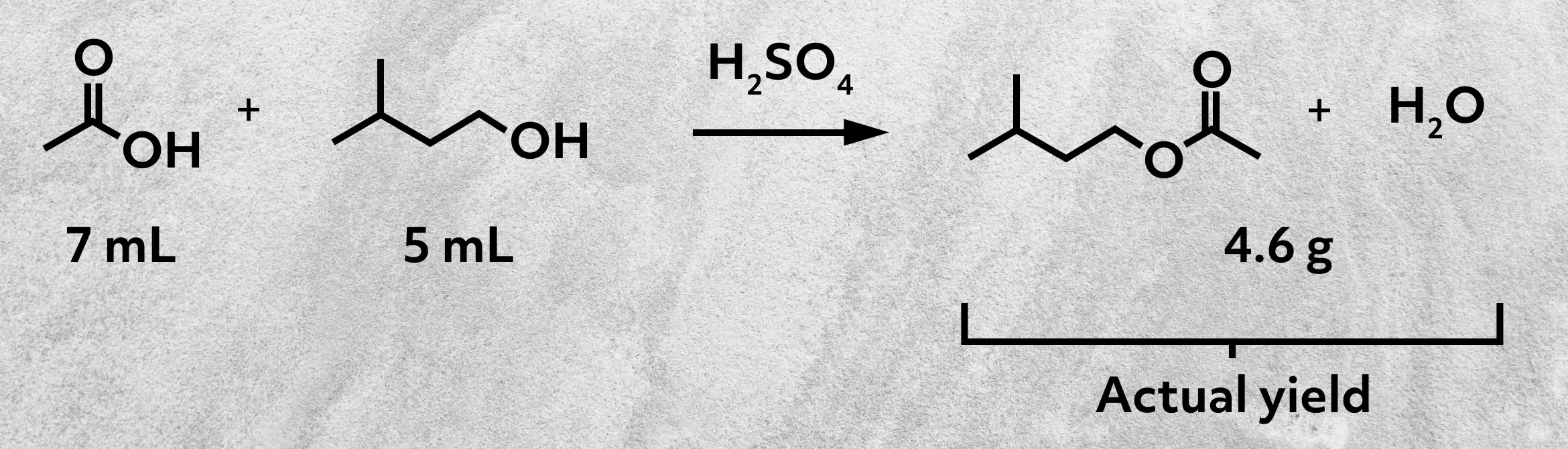
So to calculate the percent yield for this reaction, we first need to know the theoretical yield. To do that, we’ll need to examine the chemical equation.
Notice that (very importantly) this reaction is already balanced. To make one molecule of banana oil, we need one molecule of acetic acid and one molecule of isopentyl alcohol. In other words, the mole ratio is 1:1 for both reactants.
This will be necessary later when we convert from moles of reactants to moles of product.
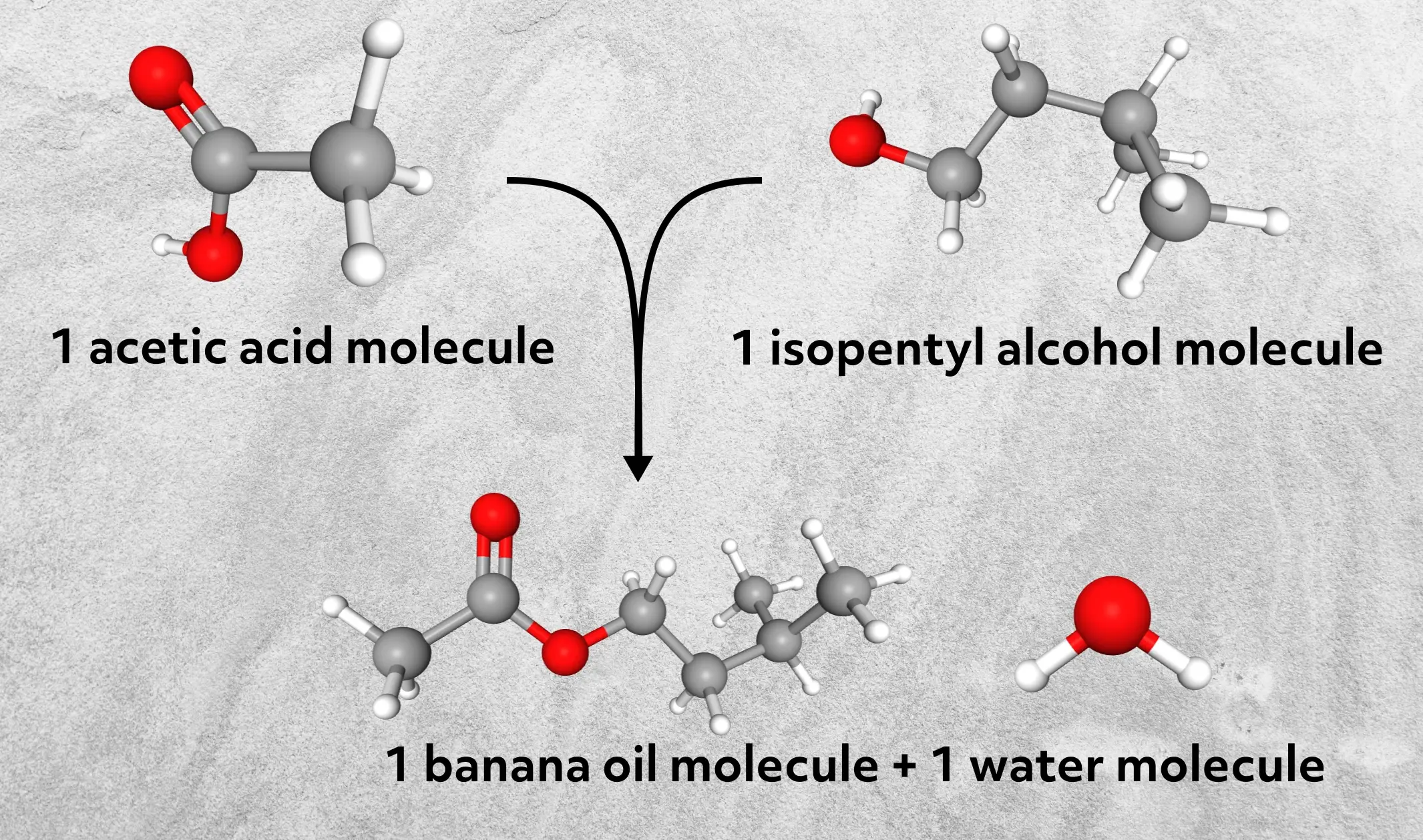
Next, we need to know how much banana oil we can make from 7 mL of acetic acid and 5 mL of isopentyl alcohol – our theoretical yield. Your initial instinct might be, well, 7 plus 5 is 12, so we’ll make 12 mL of banana oil. While that addition checks out, the chemistry doesn’t. We need to know exactly how many moles of product are made in the reaction to give a chemically accurate answer. To do that, we need to know the mole amounts of both reactants.
To calculate the number of moles for each reactant, we just need to do some conversion work. First, we convert from volume to mass using their densities, then from mass to moles using their molar masses.
So here’s our conversion for acetic acid: We have 7 mL of acetic acid, and we need to first multiply by our conversion factor 1.05 grams per mL to convert to grams of acetic acid. Then, we need to convert to moles, so we will multiply by the conversion factor 1 mole is 60.052 grams.
When we multiply all this out, it gives us 0.12 moles of acetic acid.
Here’s the conversion for isopentyl alcohol: We have 5 mL of isopentyl alcohol and we are going to multiply this by the conversion factor of grams per mL of isopentyl alcohol, or 0.8104 grams per mL. Then we are going to convert to moles. 1 mole of isopentyl alcohol is equal to 88.148 grams of isopentyl alcohol, so we will multiply by 1 mol over 88.148 grams. This results in 0.046 moles of isopentyl alcohol.
Remember, always double-check to make sure your units are cancelling appropriately!
For both acetic acid and isopentyl alcohol, given that we know their molecular formulas, we could have calculated their molar masses. However, without the chemicals, graduated glassware, and a scale, we can’t calculate their densities. But fortunately, density is a well-reported physical characteristic that’s easy enough to find online – just make sure that you have the correct units.
All right, so now we compare the moles of acetic acid and isopentyl alcohol. Note that the moles of each reactant directly correspond to how much banana oil each could make. This is because their mole ratios are 1:1. We can rigorously show this by converting the moles of reactant to moles of product using the mole ratio. This isn’t very exciting because the ratio is 1 to 1, but this step is vital in more complex reactions.
0.12 moles of acetic acid times 1 mole of banana oil over 1 mole of acetic acid equals 0.12 moles of banana oil.
0.46 moles of isopentyl alcohol times 1 mole of banana oil over 1 mole of isopentyl alcohol equals 0.046 moles of banana oil.
\(0.046\text{ moles isopentyl alcohol}\frac{1\text{ mole banana oil}}{1\text{ mole isopentyl alcohol}}=0.046\text{ moles banana oil}\)
Identifying the Limiting Reagent
From these calculations, we find that we can make a lot more banana oil with the acetic acid than the isopentyl alcohol, which means that our reaction is ultimately limited by the isopentyl alcohol.
We’ve just identified isopentyl alcohol as our limiting reagent – the reactant that will determine the theoretical yield of our product. So even though we have 0.12 moles of acetic acid, at most, we can only make 0.046 moles of banana oil because that’s how much isopentyl alcohol we have.
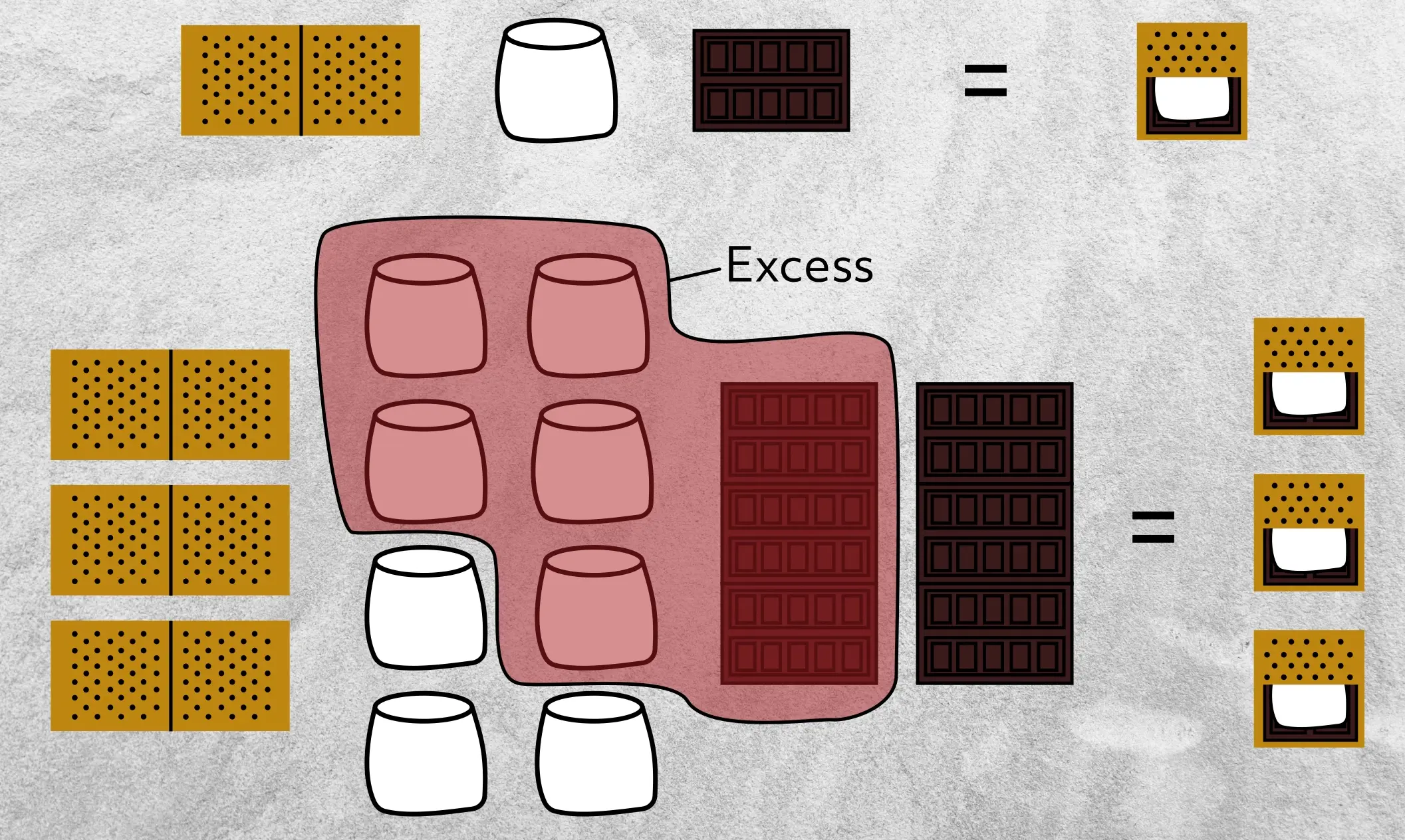
Let’s stop and take a second to think about limiting reagents because it’s a really important concept. An easy and relatable way to understand limiting reagents is to consider s’mores. For each s’more, we need 1 graham cracker, 1 marshmallow, and 1/3 of a chocolate bar.
Say we have three graham crackers, eight marshmallows, and two chocolate bars. How many s’mores can we make? The answer is 3 because we only have three graham crackers and we need one graham cracker for each s’more. So even though we have more marshmallows and chocolate, we still can only make three s’mores with three graham crackers.
This means that graham crackers are the limiting reagent and that we’ll be left with excess marshmallows and chocolate, which, to be honest, I’m not complaining about.
Catalysts and Limiting Reagents
One last note about limiting reagents before we return to calculating the percent yield. You might remember that we added sulfuric acid to our banana oil reaction but didn’t check to see if it was the limiting reagent. Well, sulfuric acid was added as a catalyst, which means that it’s regenerated after each use—so it could never be the limiting reagent.
That is why it is listed above the reaction arrow and not with the reactants. This is true for all catalysts, so for future problems, you never need to consider the catalyst as a potential limiting reagent.
Final Percent Yield Calculation
Alright, so back to our reaction in the lab. We now know that, if everything goes perfectly, we at most can make 0.046 moles of banana oil. But wait! We didn’t measure the moles of our banana oil in the lab, we took its mass, so we’d better convert those moles to grams using the molar mass of isopentyl acetate. 0.046 moles of isopentyl acetate times 130.19 grams per 1 mole of isopentyl acetate is equal to 5.98 grams of isopentyl acetate.
\(0.046\text{ moles isopentyl acetate }(\frac{130.19\text{ grams}}{moles}= 5.98\text{ grams isopentyl acetate}\)
Okay, we now know that the theoretical yield for our reaction is 5.98 grams of banana oil, which means we can finally calculate our percent yield!
Remember, percent yield equals the actual yield divided by the theoretical yield times 100%, which gives us 77%. Which isn’t too bad, but it’s not great. Ideally, we want the percent yield of a reaction to be higher to avoid wasting resources and energy.
Whenever you find yourself with a low percent yield, it’s always good to reflect on why that happened. Maybe you lost a lot of product during extraction or purifying steps. Or maybe there’s a competing side reaction that produces a different product. Maybe we didn’t allow the reaction enough time or provide enough energy or maybe the chemical equilibrium lies close to the reactants. The reasons will vary from reaction to reaction, so some critical analysis will be necessary.
Also, note that we did make an assumption about the mass of our product. We assumed that it was 100% banana oil. But what if there was some leftover acetic acid in our product (after all, we added it in excess)? Or maybe some water since that was a product too.
Basically, without further testing, we don’t know the purity of our product; we’re just assuming that it’s 100% banana oil. So if anything, we may be overestimating our actual yield. In fact, you could find yourself with a percent yield greater than 100%, which should be impossible, and often indicates that either your calculations are incorrect or your product is heavily contaminated.
Review and Practice
Alright, before you try an example on your own, let’s review the steps we took to calculate the percent yield for our banana oil reaction.
- First, we went to the lab, ran the reaction, and found our actual yield.
- Second, we calculated the theoretical yield. To do this, we converted our reactants to moles, and then using the mole ratio from the balanced chemical equation, converted to theoretical moles of product. Using those values, we identified the limiting reagent, and converted from moles of product to mass of product – this is our theoretical yield.
- Third, knowing both the actual and theoretical yield, we then calculated the percent yield.
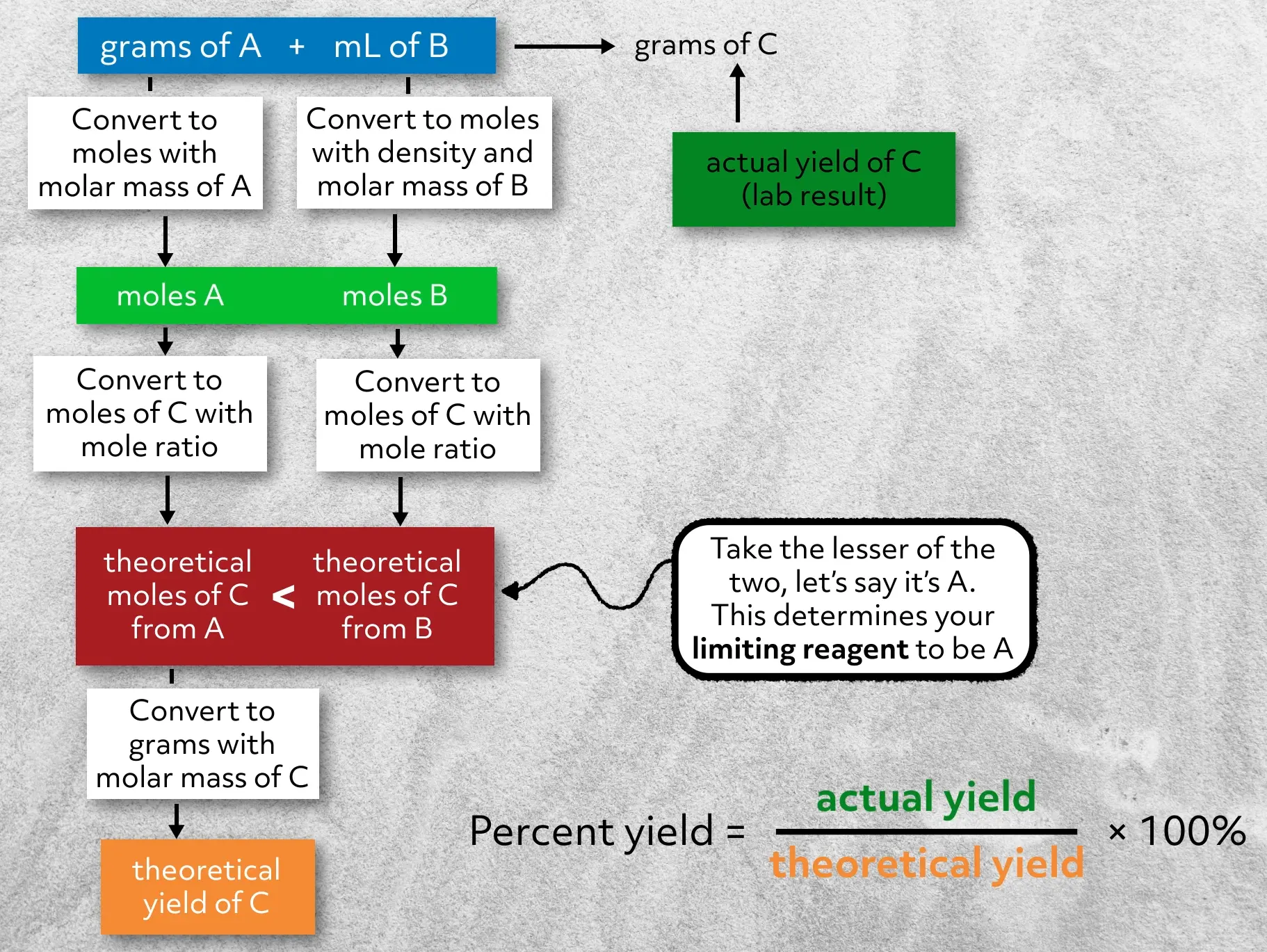
This is the general flow that you’ll use to calculate the percent yield for any reaction. Always make sure that your chemical equation is balanced and that the units cancel during your conversion steps. And lastly, when you’re actually in the lab, you should always think critically about your yield. First, is it between 0 and 100% (if it’s not, you have a problem)? And second, if your yield is low, what might have contributed to that and how could you improve it?
So now it’s time for you to give it a try. Here is the reaction for the formation of silicon carbide from silicon dioxide and powdered carbon with the necessary information to calculate the percent yield: SiO2(s) + 3C(s) -> SiC(s) + 2CO(g).
200.0 kg of sand (silicon dioxide – SiO2) is reacted with 150.0 kg of powdered carbon to form 112.4 kg of silicon carbide (SiC), a ceramic material, along with carbon monoxide. What is the percent yield of silicon carbide?
SiO2 – 60.08 g/mol
C – 12.01 g/mol
SiC – 40.10 g/mol
CO – 28.01 g/mol
Pause the video and take a second to solve it. Make sure to determine which reactant is the limiting reagent!
First, to calculate the theoretical yield, we must determine which reactant is the limiting reagent. To do that, we convert the kilograms of each reactant to moles of product using unit conversion, the molar masses, and the mole ratios.
\(150.0\text{ kg C}(\frac{1000\text{ g}}{1\text{ kg}})(\frac{mol\text{ C }}{12.01\text{ g C}})(\frac{1\text{ mol }SiC}{3\text{ mol }C}=4163\text{ mol }SiC\)
From this calculation, we see that silicon dioxide is the limiting reagent. Now to convert moles of silicon carbide to kg. 3,328 moles of silicon carbide, times 40.10 grams of silicon carbide per mole of silicon carbide, times 1 kilogram over 1,000 kilograms is equal to 133.5 kilograms of silicon carbide.
So, our theoretical yield is 133.5 kg of SiC. Now to calculate the percent yield, we simply divide our actual yield, 112.4 kg, by the theoretical yield and multiply by 100%.
So the percent yield is 84.19%. Hopefully, that’s what you got too!
I hope this overview was helpful! Thanks for watching, and happy studying!