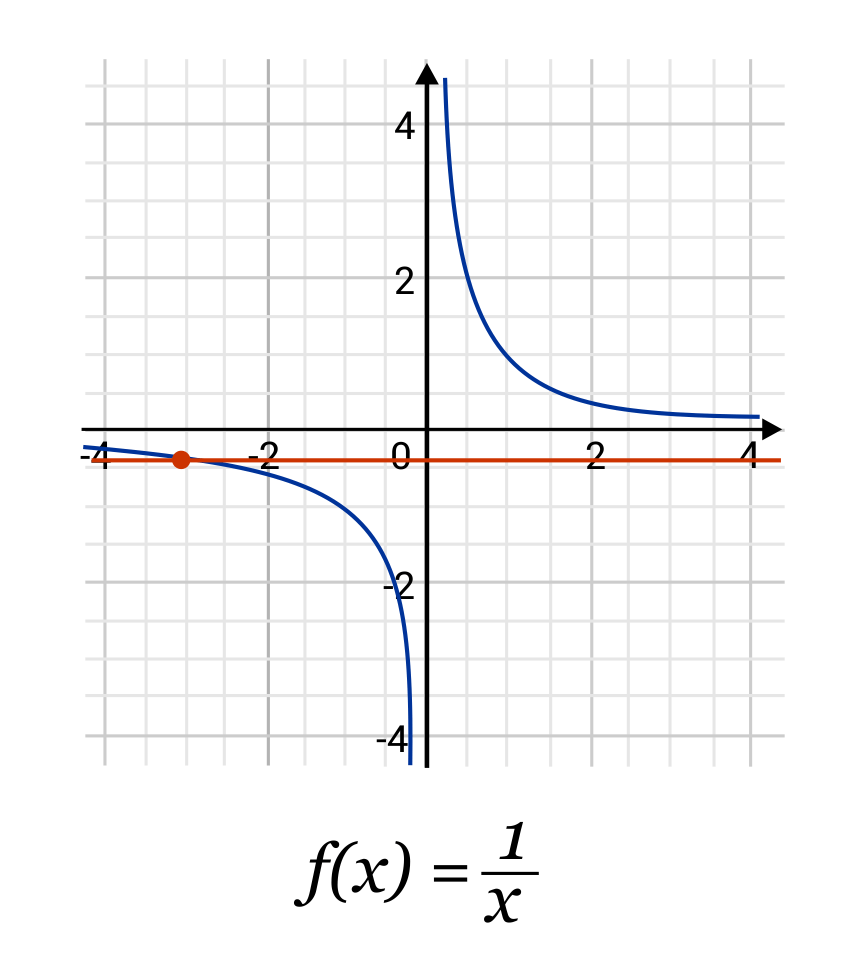What is a One-to-One Function?
We say that a function \(f(x)\) is one-to-one if for all \(x\)-values, there are unique y-values, or equivalently, there are unique \(f(x)\)-values. An easy way to visualize this concept is in the case of continuous functions, where they must be strictly increasing or strictly decreasing to be considered one-to-one.
How to Determine if a Function is One-to-One
The formal method we use to show that a function is one-to-one is as follows:
Select two values, \(a\) and \(b\), on the \(x\)-axis, and determine the \(y\)-values \(f(a)\) and \(f(b)\) that the function gives us at those two points. If the two outputs \(f(a)\), \(f(b)\) are different from each other (that is, not equal to each other) for all pairs \(a\) and \(b\), then the function is one-to-one.
Sometimes we use illustrations to describe how one set maps to another in order to see if it is one-to-one. Consider the following sets of numbers: A={1,2,3}, B={1, 2, 3, 4, 5, 6}. Suppose we have a function that maps from Set A into Set B in the following way:
This function essentially gives us the ordered pairs \((1,2)\), \((2,4)\), and \((3,6)\). Clearly, all of these have unique y-values, and in the illustration, we see that no two arrows point to the same number in B. For those reasons, we know that the function described is one-to-one.
Another method for determining if a function is one-to-one is the horizontal line test, which you may recognize as very similar to the vertical line test we used in Algebra to validate functions. When viewing the graph of a function, draw or imagine a straight horizontal line passing over the coordinate plane. If at any point, that line intersects the function in more than one place, the function fails the test and it is not one-to-one.
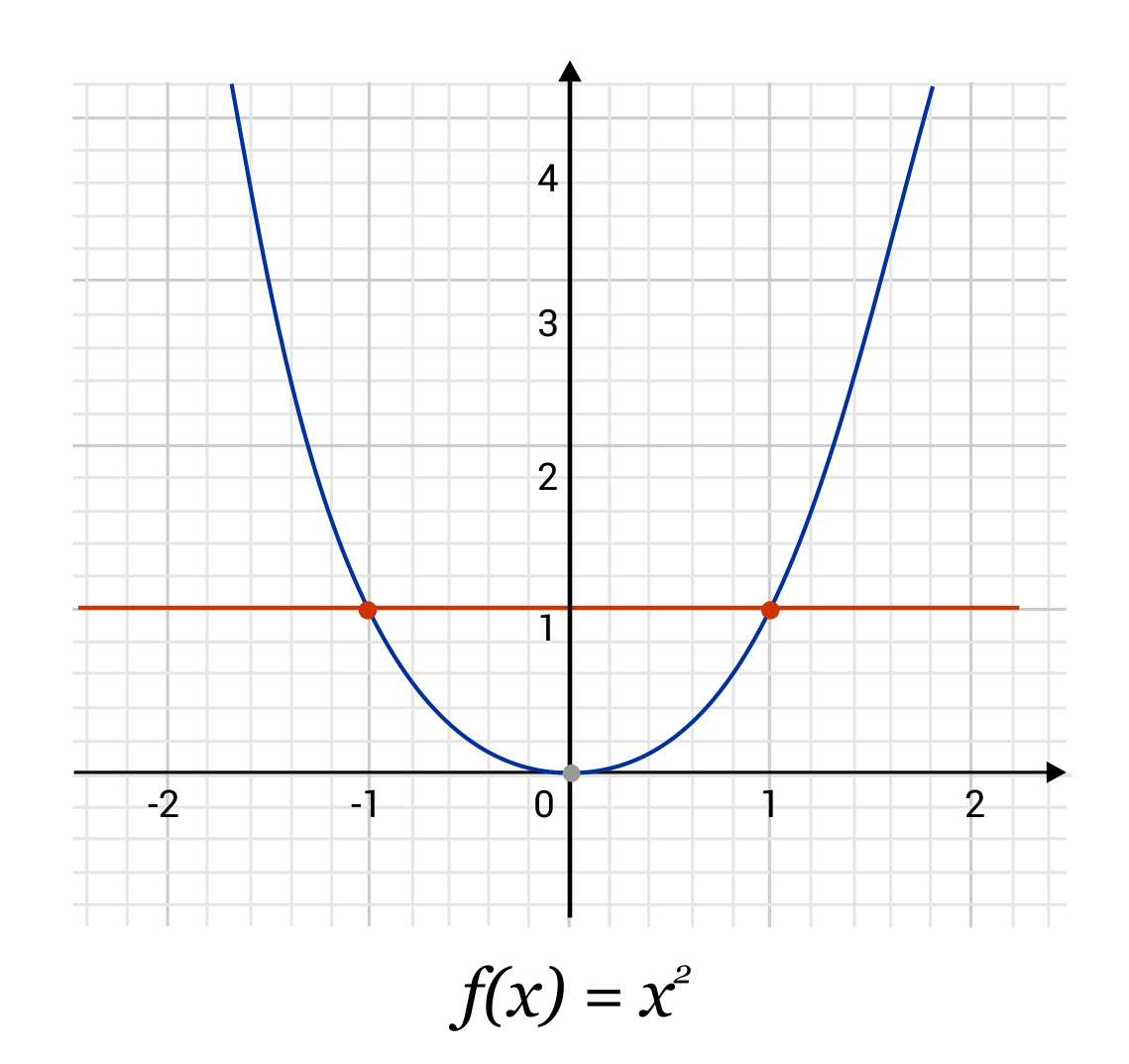
For example, it is easy to see that the functions \(f(x)=x^2\) and \(f(x)=x^3+x^2\) are not one-to-one by using the horizontal line test. For both functions, we can find at least one place where a horizontal line intersects the function more than once.
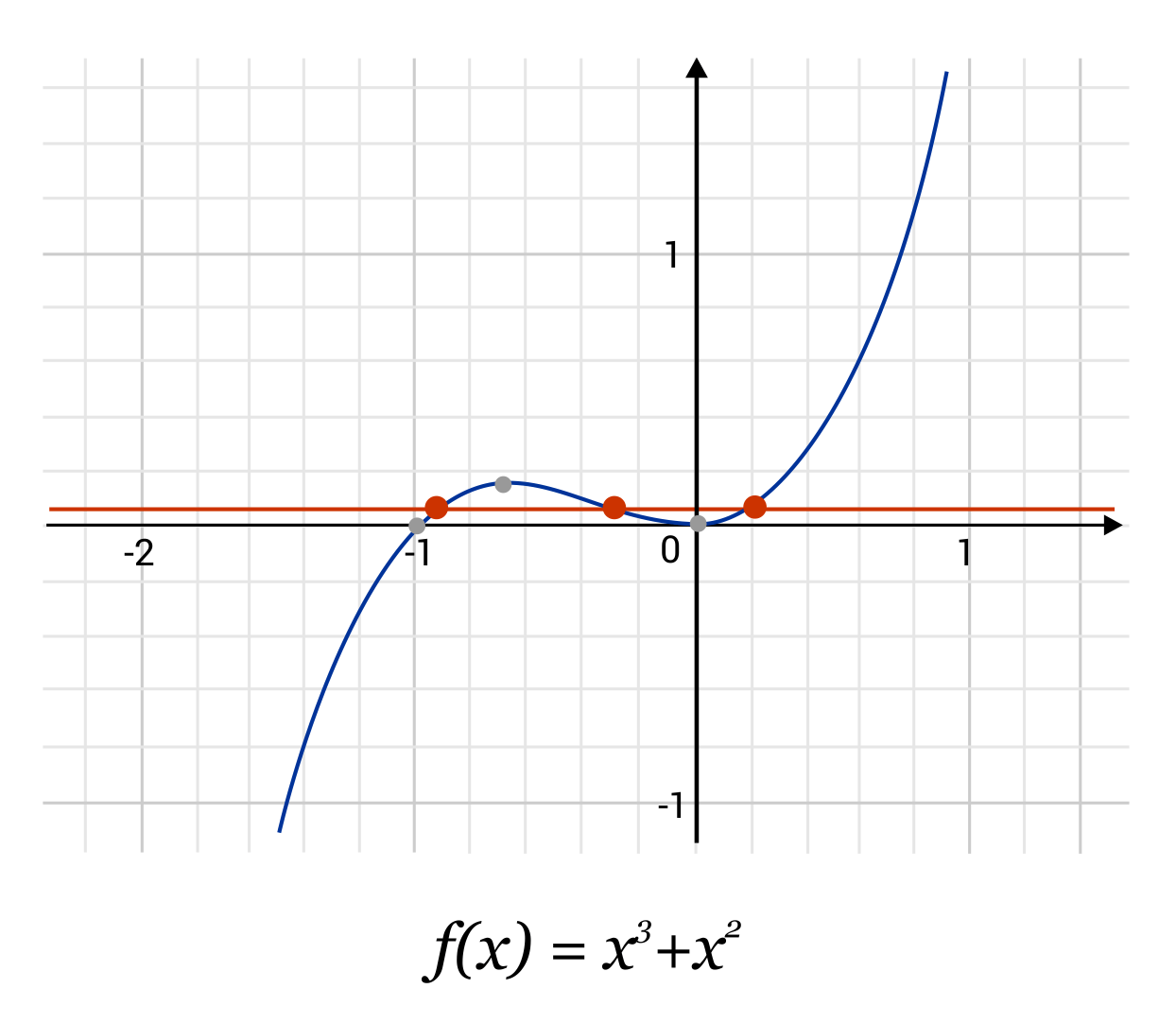
Some functions that do pass the horizontal line test include \(f(x)=x\) and \(f(x)=frac{1}{x}\). It may seem pretty obvious by looking that \(f(x)=x\) is one-to-one. But what about \(f(x)=frac{1}{x}\)? Even though this function has asymptotes that get closer and closer to \(y=0\), each x still gives a unique y-value, and the horizontal line never intersects the function more than once, no matter where we put it.
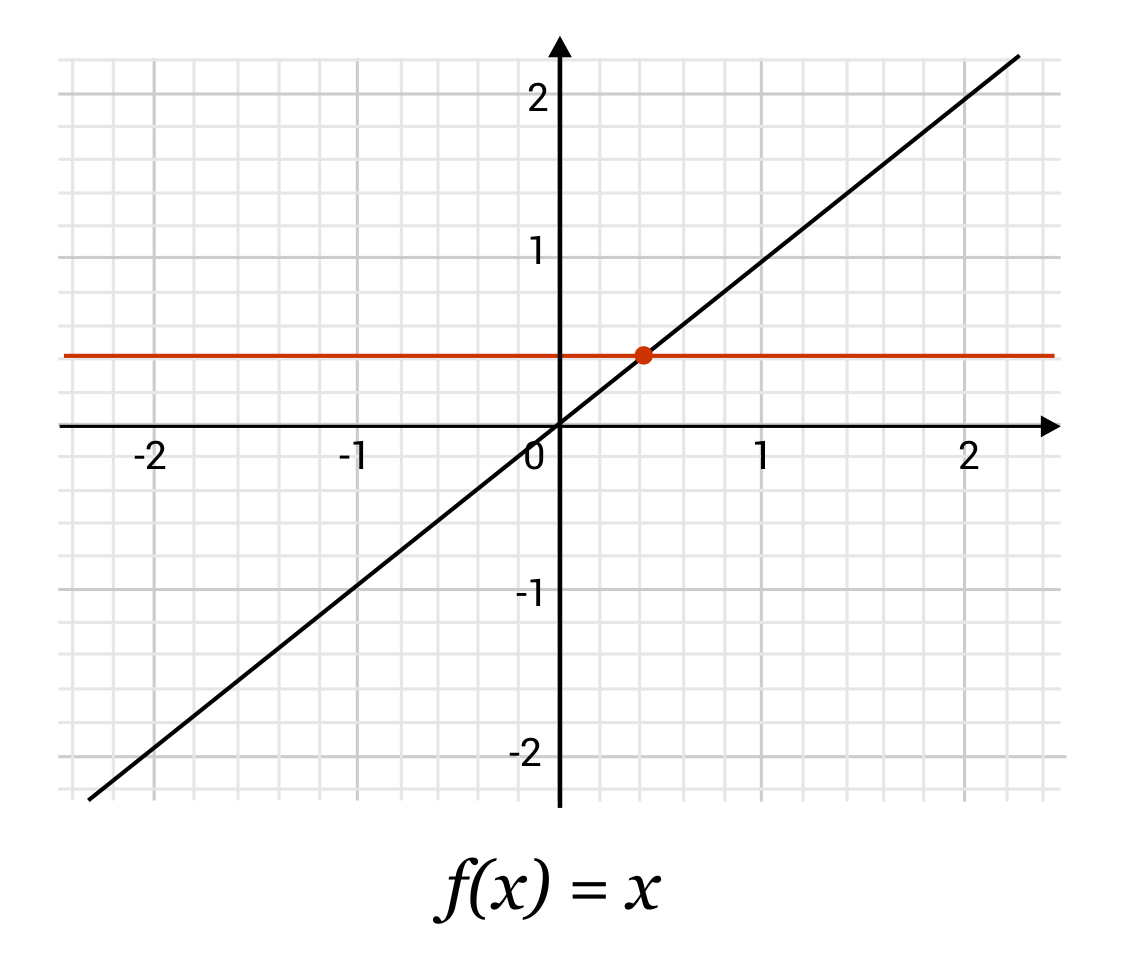
One-to-one Function Sample Questions
Here are a few sample questions going over one-to-one functions.
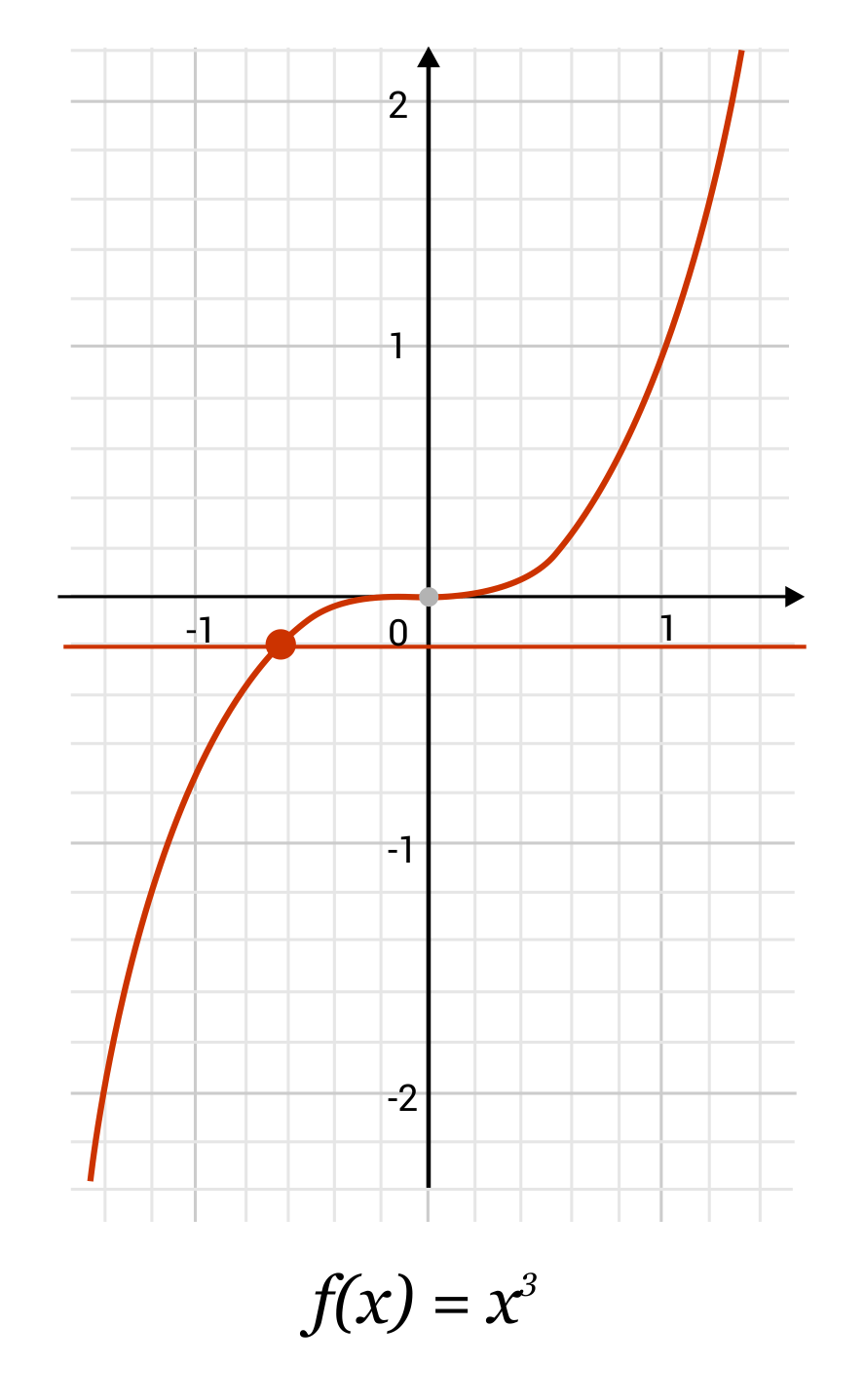
Using the horizontal line test, determine whether the function \(f(x)=x^3\) is one-to-one.
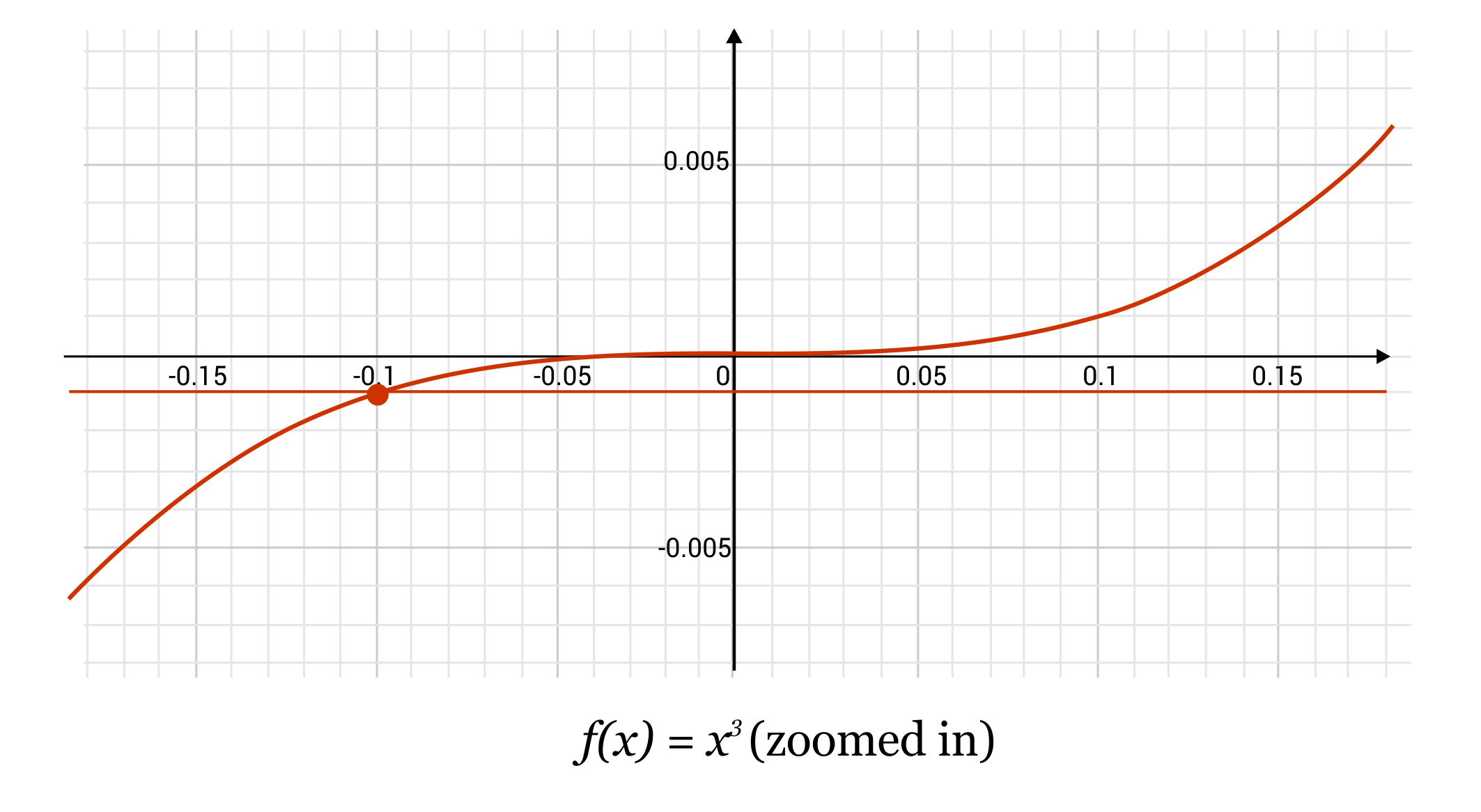
When we look at this function on the coordinate plane, we see the function as it appears below. On the left, it may be harder to tell that the function passes the horizontal line test because of how closely it hugs \(y=0\) near the origin. However, when we zoom in (see last image), it becomes more clear that the function will only ever touch 0 at the origin. The function \(f(x)=x^3\) passes the horizontal line test.
Determine whether the following function is one-to-one:
The function is not one-to-one. Because there is a number in Set Y which has two arrows pointing to it, two separate values from Set X map to the same value in Y, and we see that that value is not unique.
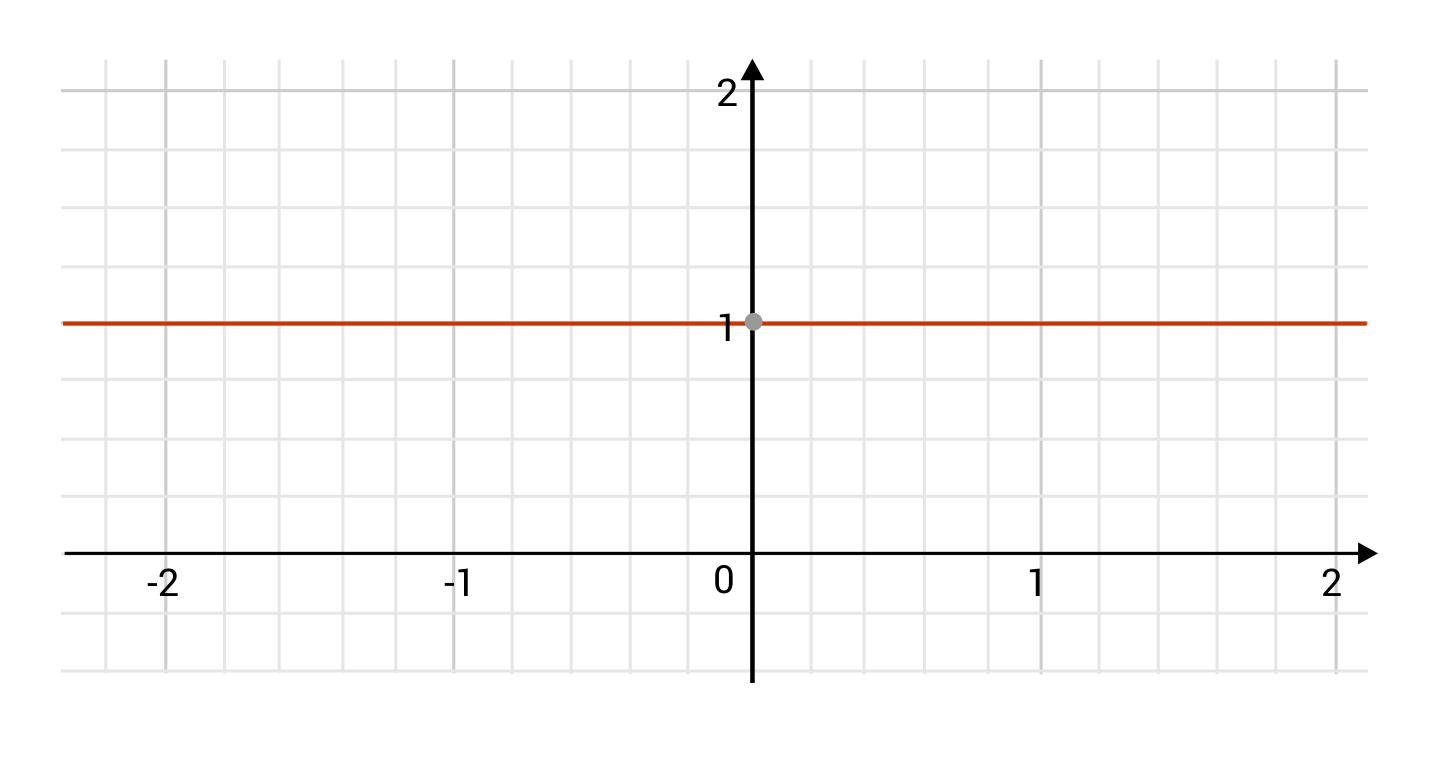
Use the horizontal line test to determine whether the function \(f(x)=1\) is one-to-one.
The function is not one-to-one. Look at the graph for \(f(x)=1\). The function itself is a horizontal line. If we were to draw another horizontal line on top of the function, it would intersect the function at all points! That’s certainly more than a single point. This function fails the horizontal line test, and therefore the function is not one-to-one.
Determine whether the following function is one-to-one:
The function is one-to-one. Because each element of Set X maps to a unique element of Set Y, no two arrows point to the same number, and the function is therefore one-to-one.
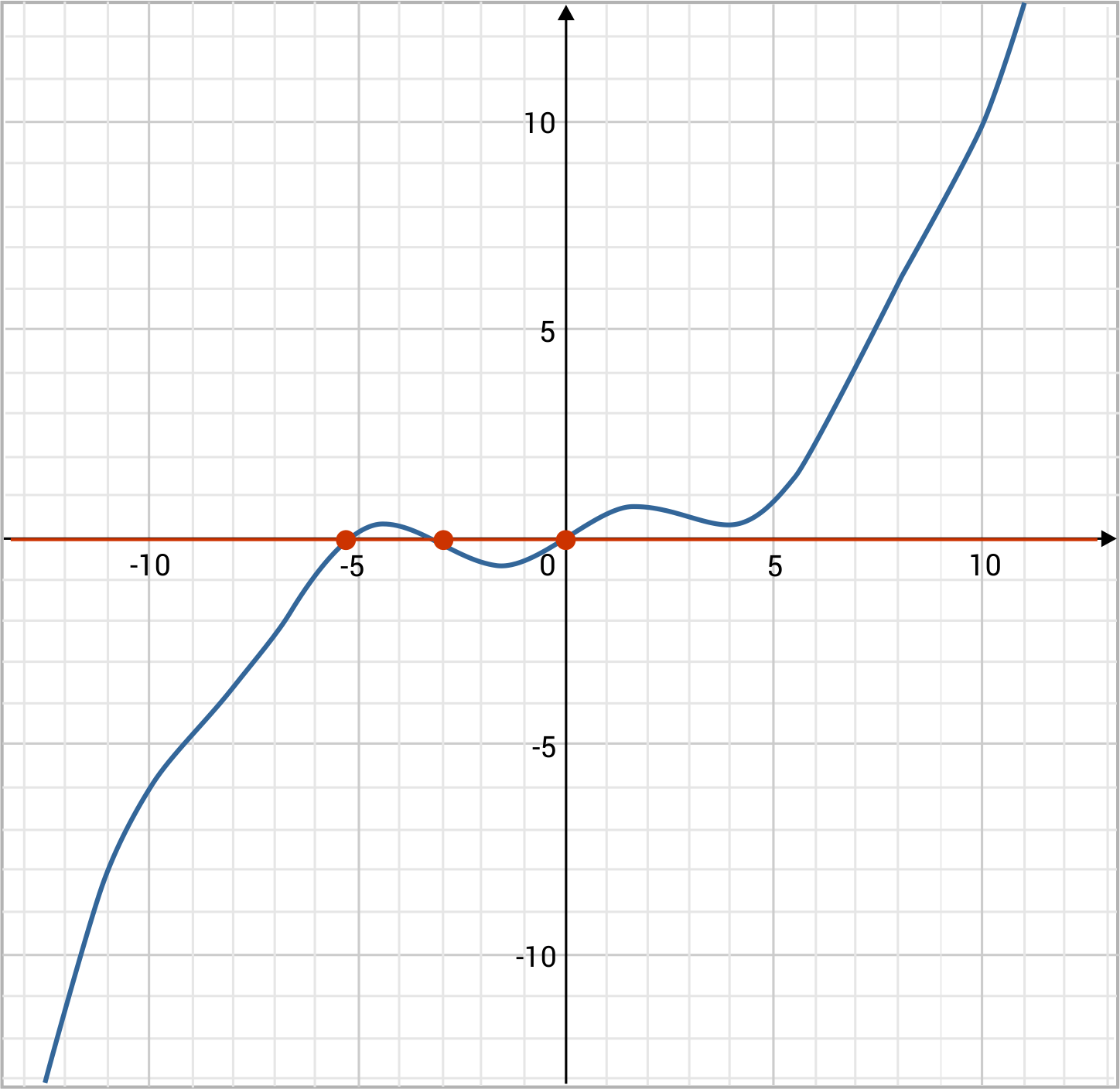
Observe the following plot of function \(f(x)\) and use the horizontal line test to determine whether or not it is one-to-one.
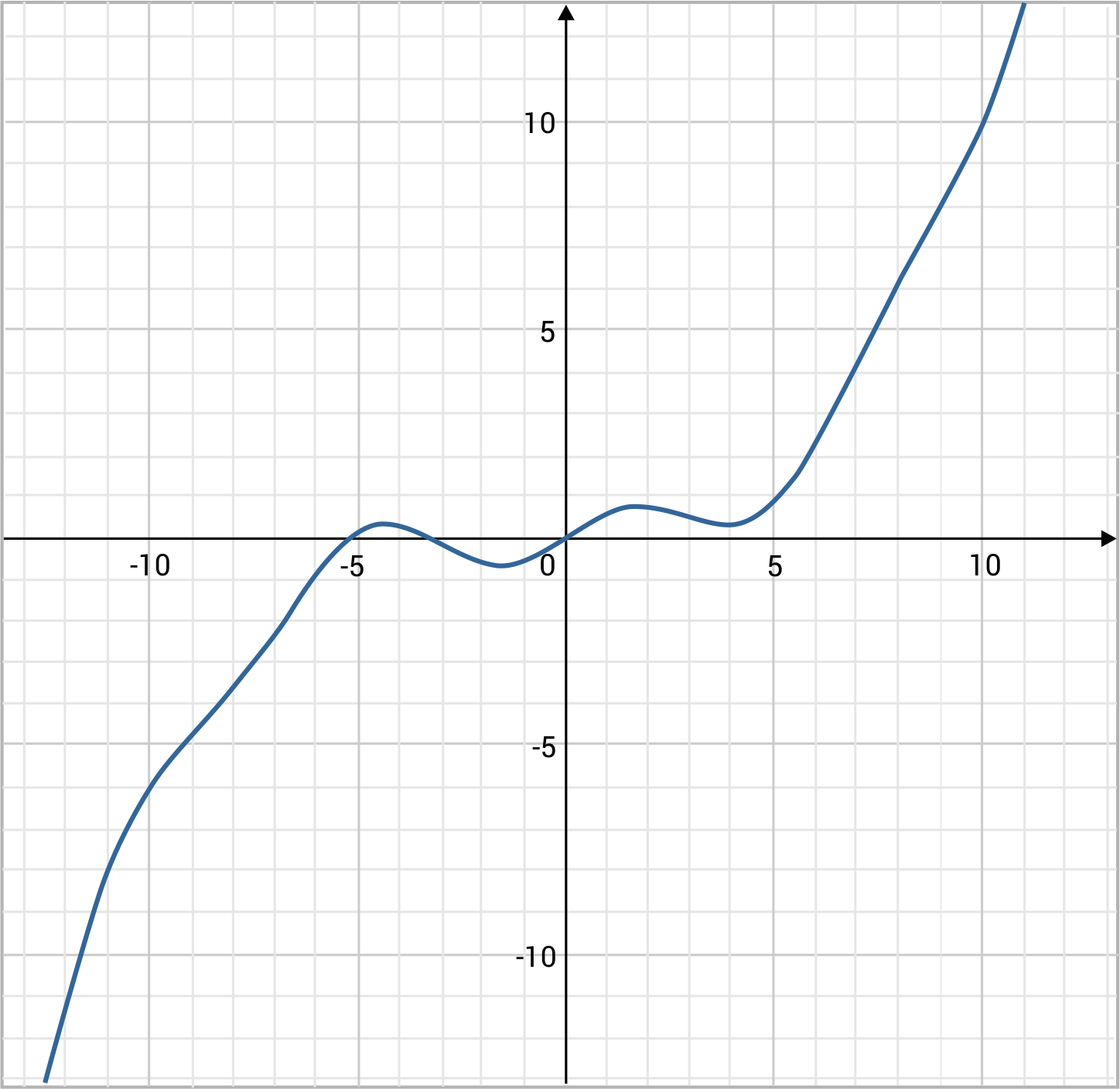
The function is not one-to-one. Even though on the left and right sides of the plot, the function appears to be strictly increasing, we see near the origin that there is some wavering. When we draw a horizontal line near the origin, we see that the function passes through it more than once. Therefore, the function fails the horizontal line test and is not one-to-one.