
Hi, and welcome to this video on Newton’s second law of motion! In this video, we will look at Newton’s second law, compare it with his first law, and look at a couple of simple, common applications. Let’s get started!
What is Newton’s Second Law of Motion?
Newton’s second law states the acceleration of an object is directly proportional to the net external force applied, and it is indirectly proportional to its mass. In other words, more force generates more acceleration for a given mass, but more mass means less acceleration from a given force.
Newton’s second law is generally written in the form \(F=ma\), where \(F\) is the net external force causing a mass, \(m\), to undergo an acceleration, \(a\). Since \(m\) is a positive quantity, the acceleration vector points in the same direction as the net external force vector.
Newton’s second law can be considered an extension of the first law for the situation where the sum of the net external forces is non-zero. As with Newton’s first law, the internal forces are not included, and it can only be applied in an inertial frame of reference.
Application in Multiple Dimensions
Let’s take a look at both a one-dimensional and a two-dimensional example to illustrate some applications of Newton’s second law.
1D Example
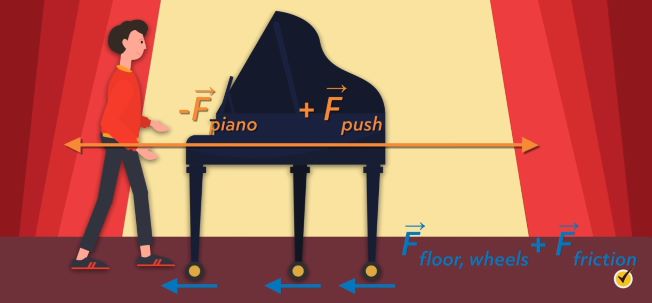
Let’s say you have someone pushing a piano across a stage. In this example, we are interested in the moment when the person pushes the piano with just enough force to get it moving.
Let’s set up the situation in which the first law holds; that is, the situation of translational equilibrium.
The forces in the \(y\)-direction, as we have seen, are the force of gravity downward and the force of the floor pushing up. In the \(x\)-direction, we have the push force of the person in the positive \(x\)-direction and the force of the piano pushing back in the negative \(x\)-direction.
When the person pushes with enough force to overcome the frictional forces resisting motion, the piano goes from a zero velocity to a non-zero velocity, and any change in velocity constitutes an acceleration.
Thus, during the time when the velocity is changing, the net external force causes an acceleration, and Newton’s second law comes into play.
For the sake of completion, let’s toss some numbers into our equation to get an idea of the numerical value of the acceleration.
Let’s say the frictional force between the wheels and the floor is 10 Newtons and the total friction in the bearings of the wheels is 10 Newtons. Using Newton’s first law for the x-direction, we can calculate the net frictional force to determine the minimal force the person must push with.
Newton’s first law tells us that any pushing force greater than 20 Newtons will get the piano moving. While the person may not have made the numerical calculation we did, they intuitively knew they had to push with a force greater than the number we calculated.
So let’s say they push with a force of 30 Newtons and calculate the acceleration using Newton’s second law, assuming the piano has a mass of 200 kg. Restating Newton’s second law as the sum of the external forces in the \(x\)-direction is equal to the push force minus the force of the piano pushing back, substituting in the values we discussed, and solving for the acceleration yields a value of \(0.05\text{ m/s}^{2}\) for the acceleration.
\(\frac{10\text{ }N}{200\text{ }kg}=\text{ }a\)
\(0.05 \text{ }\frac{m}{s^{2}}=\text{ }a\)
We just used Newton’s second law to calculate the acceleration of the piano, in one direction, given the external forces. Now that we know the acceleration, assuming it is constant based on the constant external forces applied, we could use the equations of motion with constant acceleration to calculate the time of travel, and final velocity, given the initial velocity and initial and final positions.
In fact, given those three equations of motion for constant acceleration, you can find any three unknowns given the other parameters.
2D Example
Let’s take a look at a 2D example using Newton’s second law. In this example, we will also use a static inertial frame of reference fixed on the origin of our mass.
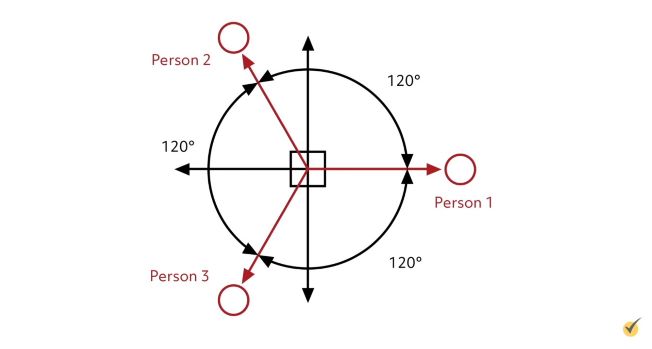
Imagine you’re involved in a three-way tug-of-war. Each person is 120 degrees from the other, and the \(x\)-axis is lined up with one of the “warriors.”
Imagine, initially, each person pulled with equal force, and there is no motion, so Newton’s first law applies. We can use vector math to show the force components from each person in the \(x\) and \(y\)-directions, starting with the person on the right. We can see all of their force is directed in the \(x\)-direction, so the force in the \(y\)-direction is zero.
The force from person 2 has components in the \(x\)– and \(y\)-directions, as shown. Similarly, the force from person 3 must be broken down into its \(x\)– and \(y\)-components, as shown.
If we state Newton’s laws for the three forces, we can see that Newton’s first law holds.
| Person | Forces in x-direction | Forces in y-direction |
|---|---|---|
| 1 | F | 0 |
| 2 | \(F\text{ }cose(120^{\circ})=F(-\frac{1}{2})\) | \(F\text{ }sin(120^{\circ})=F(\frac{\sqrt{3}}{2})\) |
| 3 | \(F\text{ }cose(240^{\circ})=F(-\frac{1}{2})\) | \(F\text{ }sin(240^{\circ})=F(\frac{\sqrt{3}}{2})\) |
\(F_{(net_y\ )}=F_{(P1_y\ )}+F_{(P2_y\ )}+F_{(P3_y\ )}\)
\(F_{net_x}=F+F(-\frac{1}{2})+F(-\frac{1}{2})=0\)
\(F_{net_y}=0+F(\frac{\sqrt{3}}{2})+F(-\frac{\sqrt{3}}{2})=0\)
Let’s say that the person aligned with the \(x\)-axis impulsively pulls with a force 1.3 times the force of the others. Using Newton’s second law, we can calculate the acceleration of the center and the two people on the left.
Let’s assume that each person has the same mass of 50 kg and the rope has negligible mass. The mass of the system is then 150 kg. Now, let’s say that \(F\) is equal to 100 Newtons. Substituting those values into the force equation in the \(x\)-direction, and simplifying, we can calculate the acceleration.
\(F_{net_y}=0+F(\frac{\sqrt{3}}{2})+F(-\frac{\sqrt{3}}{2})=0\)
\(0.3(100 \text{ }N)=150\text{ }kg\times a\)
\(\frac{30}{150}\text{ }m/s^{2}=a\)
\(0.2 \text{ }m/s^{2}=a\)
Intuitively, we know the direction of the acceleration is along the positive \(x\)-axis, and Newton’s Second Law gives the quantitative value for the acceleration, which we calculated to be zero point two meters per second squared.
We just saw simple one- and two-dimensional applications of Newton’s second law. When applying these principles to more complex examples, keep in mind that the concepts are the same, but the algebra may be a little more involved. Nonetheless, Newton’s laws can be used to calculate the motion of all bodies in space, as long as they are moving in an inertial frame of reference.
To wrap things up, let’s go over a few review questions!
Review Questions
1. True or False: Unlike Newton’s first law, Newton’s second law is valid for bodies in motion in both inertial and non-inertial frames of reference.
2. True or False: Newton’s second law is only valid for bodies with constant acceleration.
3. Calculate the acceleration of the body in the diagram given the parameters indicated, assuming the mass is not lifted from the ground. Also calculate the force from the floor.
And here is the correct calculation of the force from the floor:
That’s all for this review. Thanks for watching, and happy studying!