What is Newton’s First Law of Motion?

Hi, and welcome to this review of Newton’s first law of motion! In this video, we’ll see how it forever changed people’s perceptions of how and why things move. Let’s get started!

Understanding how and why things move has been the goal of scientists for thousands of years. Over time, calculations and experiments helped pave the way for a deeper understanding of motion, with Galileo Galilei defining the laws of gravity in the 1580s and Johannes Kepler penning his laws of planetary motion in 1618. The basis of our current understanding of motion comes from Sir Isaac Newton’s three laws of motion, which he established in 1687. In this video, we’ll be discussing his first law of motion, also known as the law of inertia.

Newton’s first law of motion states that an object at rest will stay at rest, and an object in motion will stay in motion unless acted on by a net external force.

This statement is much more intuitive than it sounds. One of the key things to remember, though, is that this law is only valid for objects in an inertial reference frame. An inertial reference frame is a frame of reference that is moving at a constant velocity.

Let’s think of it this way. When you kick a soccer ball, and it soars through the air, the soccer ball isn’t the only thing that’s moving. Remember, we’re on a planet that’s rotating at about 1,000 miles per hour, our solar system is moving at about 140 miles per second, and our galaxy is rotating at 130 miles per second. So objects that we consider to be “stationary” on Earth are technically moving at a speed of almost 1 million miles per hour!

However, it’s generally pointless to include the motion of things like the solar system and Earth when we talk about the motion of things on Earth, like cars or people. What we do instead is use Earth as a point of reference, or an inertial reference frame; that is, we discuss the motion of objects in reference to Earth.

Let’s take a look at an object in an inertial reference frame that has a velocity of zero.

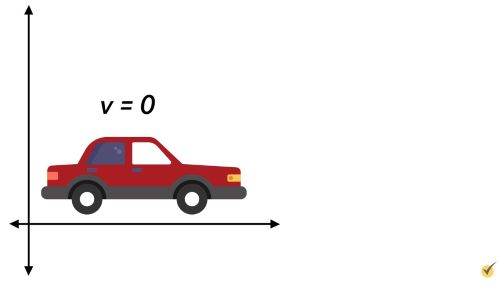
It would seem that there are no net external forces acting on the car since the car isn’t moving. But what about gravity? Isn’t that an external force? While it’s true that gravity is pulling the car downward toward Earth, the car is on the ground and the ground is providing a force in opposition to gravity. This force is called the normal force.

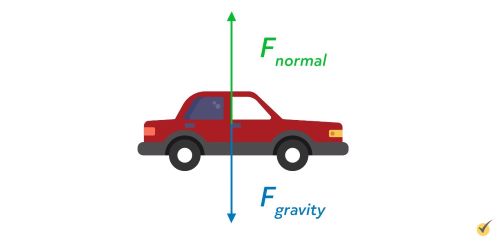
Since you have two equal forces acting in opposite directions, the forces cancel out, meaning that the car does not move in the vertical direction.

We define force by the symbol \(F\), noting the force is a vector, which means it has both magnitude and direction. By doing this, we can state Newton’s first law, mathematically, as the sum of the external forces is equal to the upward force of the ground on the car minus the downward force of gravity on the car, which is equal to zero.

\(\sum F_{ext}=F_{normal}-F_{gravity}=0\)

Note that the negative sign in front of the force of gravity indicates the downward direction of the force of gravity. This implies that the upward force is equal to the downward force.

Now, let’s imagine that someone comes along and pushes the car for a moment, providing an external force, and giving it a small velocity.

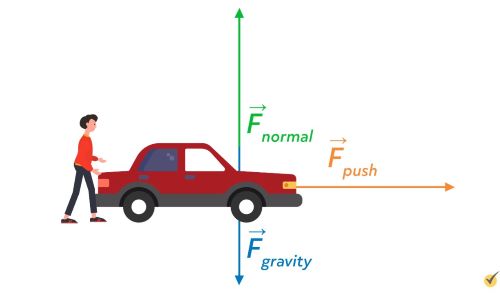
According to Newton’s first law, once the external force is removed, the car should continue to move in a straight line with a constant speed for the rest of eternity unless some other external forces come along and change its speed or direction.

Mathematically, we could state that the change in velocity with respect to time is zero.

\(\frac{\Delta v}{\Delta t}=0\)

What we’ve just described is the constant motion of an object that is in a frame of reference with zero velocity. However, what if we made the car the inertial frame of reference and discussed the motion of the passengers inside it?

Imagine if you and I were sitting in that car and there were no other objects around. In that frame of reference, you and I are not moving with respect to each other; we are both moving in the same inertial frame.

If the car changed speed or direction, you would feel it because your body wants to keep moving in the straight line with constant speed.

If we look at the head as an object moving in the inertial frame of reference of the car, if the car sped up, your head would feel like it’s being thrown backward. This is because the part of your body that is attached to the car would speed up too, but your head wants to obey the law of inertia and continue moving at a constant velocity, that is, with the same speed and direction.

Similarly, if the car were to turn to the left or the right, your head, due to inertia, would feel like it was being moved to the right or left.

Let’s look at another simple example, in which you are trying to push a piano across the stage for your performance at your high school graduation.

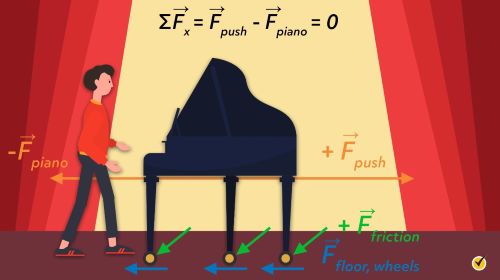
We have already discussed what the forces should be in the vertical direction, where gravity is pulling the piano down and the stage is pushing back up, so there is no net force in the vertical direction.

In the horizontal direction, along the \(x\)-axis, we can add the pushing force and note that if the piano is not moving there must be some other force pushing back against you.

We can see that the resisting force of the piano is really the frictional force between the floor and the wheels of the piano and the friction in the wheel bearings.

Since the piano has a constant speed of zero and no direction, we can state Newton’s first law as the sum of the forces is equal to the push force minus the force of the piano.

\(\sum F_{x}=F_{push}-F_{piano}=0\)

This implies that the positive push force is equal to the negative pull force from the piano.

\(F_{push}=F_{piano}\)

Review

Okay, let’s wrap things up with a few review questions.

1. Which of the following is the most accurate version of Newton’s first law?

1. An object at rest will remain at rest unless acted on by a net external force.
2. An object at rest in an inertial frame will remain at rest unless the inertial frame accelerates.
3. An object at rest in an inertial frame will remain at rest unless acted on by a net external force.
4. An object at rest or in constant motion will maintain that motion unless it is a non-inertial frame.

2. When you throw an object straight up, the object will slow down on its way up, stop for an instant, and then come back down with increasing speed and the opposite direction from its initial trajectory. Which of the following statements most accurately describes why this is the case?

1. Gravity acts upward to slow the object down on its way up and speed it up on the way down.
2. Gravity acts downward to slow the object down on its way up and speed it up on the way down.
3. Gravity only affects the object on the way down, and air resistance slows it on the way up.
4. Gravity changes direction on the object, which is the reason it slows on the way up and speeds up on the way down.

3. Which of the following reasons describes why an object would not move when you push it.

1. The law of inertia states that objects do not want to move.
2. The object is being held in place by a magnetic force that is pushing back at you.
3. Newton’s law states that the sum of all forces on a body must be equal to zero.
4. Some force is preventing the object from moving in the direction it is being pushed.

That’s all for this review! Thanks for watching, and happy studying!