Mixed Numbers and Improper Fractions
In this video, I want to discuss improper fractions and mixed numbers.
Just to review real briefly, a fraction has a numerator and a denominator. The denominator represents how many parts we’re breaking up the whole into, and the numerator (the top number) represents how many of those parts we’re counting.
If we say “three-fourths,” it means we’ve broken up this whole, whatever it may be, into four equal parts and we’re considering three of them. For instance, I’ve shaded three-fourths of this rectangle here.
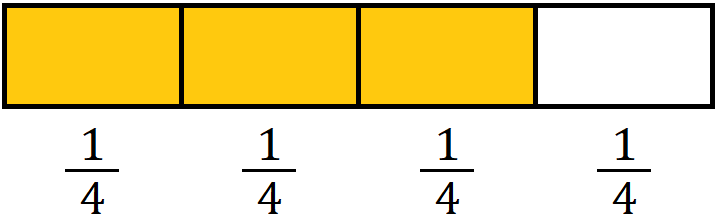
When a numerator is smaller than a denominator, or less than a denominator, we have what’s called a “proper fraction,” because the value of the fraction is between 0 and 1.
Three-fourths is a good example of a proper fraction. If the numerator is larger than the denominator, for instance, if we have \(\frac{5}{4}\), this is what’s called an improper fraction, because its value is greater than 1. For instance, if we were to try to draw this, and we had the same rectangle divided up into four parts, we could shade 1, 2, 3, 4, and then we’d run out.
We’d have to draw another rectangle to shade that fifth part.

This is considered an improper fraction. It just represents a number that’s greater than 1. It’s not really an ideal way to write this quantity. Oftentimes, what you’ll see when you have a quantity like this where it’s greater than one, you’ll see what’s called a mixed number.
The first rectangle is a whole, so we can call that 1, and the second rectangle is another \(\frac{1}{4}\). The way you’ll see it is written commonly is \(1 \frac{1}{4}\). It’s called a mixed number because you have an integer part mixed with a fractional part. Essentially, what you’re saying is 1 plus \(\frac{1}{4}\), or \(1 \frac{1}{4}\) when you have this sort of number.
Now, you can convert between improper fractions and mixed numbers pretty easily. I’ll demonstrate now how to do this. Let’s take, for instance, \(2 \frac{4}{5}\). This is a mixed number and we want to convert it now to an improper fraction. To do that, we take the denominator (5), we multiply that by the integer here (the whole number 2).
We have 5 times 2, which is 10. Then, we take that product and add to it the numerator. 10 plus 4 is 14. Then, we write 14 as our new numerator and we keep 5 as the denominator. \(2 \frac{4}{5}\) is the same as \(\frac{14}{5}\). If we want to go in reverse, we just have to do this process backward a little bit.
Let’s say we have \(\frac{12}{9}\). What we’ve got to do is divide 12 by 9. 9 only goes into 12 one time, so we take out 1 as the whole number. Subtract 9 from 12 and we’re left with 3. 12 minus 9 is equal to 3.
We’ve taken out the whole and we’ve got the 1 here, so what we’re left with is 3 of our original 12. We can write that as the remaining fraction here. We have \(1 \frac{3}{9}\).
That is how you convert an improper fraction to a mixed number.
Frequently Asked Questions
Q
What is an improper fraction?
A
An improper fraction is a fraction that represents more than one whole, where the numerator (the number on top) is greater than the denominator (the number on bottom).
Q
What is a mixed number?
A
A mixed number is a number that contains both an integer and a fraction. It represents some wholes and some parts.
Ex. \(4 \frac{1}{3}\) or \(29 \frac{3}{11}\)
Q
How do you turn an improper fraction into a mixed number?
A
Turn an improper fraction into a mixed number by dividing the numerator by the denominator. The number of full divisions becomes the whole number and the remainder becomes the numerator of the fractional part over the original denominator.
Ex. What is \(\frac{37}{11}\) as a mixed number?
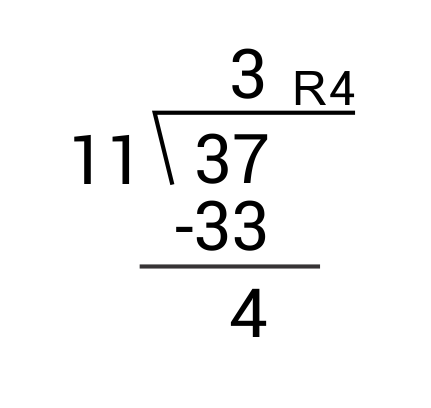
\(\frac{37}{11}=3 \frac{4}{11}\)
Q
How do you change a mixed number into an improper fraction?
A
Change a mixed number into an improper fraction by multiplying the whole number by the denominator and adding the numerator to get your new numerator and leaving the denominator the same.
Ex. \(2 \frac{7}{12}=\frac{2×12+7}{12}=\frac{24+7}{12}=\frac{31}{12}\)
Q
How do you simplify improper fractions?
A
Simplify improper fractions by dividing common factors from the numerator and denominator until there aren’t any left.
Ex. \(\frac{165}{110}÷\frac{5}{5}=\frac{33}{22}÷\frac{11}{11}=\frac{3}{2}\)
Q
How do you simplify mixed numbers?
A
To simplify mixed numbers, simplify the fractional part as necessary by dividing the numerator and denominator by a common factor. The whole number will stay the same.
Ex. \(7 \frac{2}{4}=7 \frac{2}{4} ÷(\frac{2}{2})=7 \frac{1}{2}\)