Push and Pull Forces

Hi, and welcome to this video on push and pull forces! In this video, we’ll discuss what forces are, how they work, and how to describe the pushing and pulling associated with them by using vectors. Let’s get started!

Force Equation and Vector Components

So, what exactly is a force?

Well, there are several different types of forces, but put simply, a force is a push or a pull on an object. So, when you use your energy to push or pull on an object, you are exerting a force on it. And this is just one example of force; there are different forces all around us. There are magnetic, electric, friction, and gravitational forces, with gravity being the most universally recognized example in our everyday lives. We know that the Earth’s gravity makes objects fall to the ground; however, any two objects that have a mass also have a gravitational force between them, causing an attractive pull between the objects. Outside of the influence of Earth’s gravity, these objects would move toward each other, but because Earth’s mass is very large, the force of gravity is also much larger than, say, the force between a chair and table.

This leads us to the equation used to describe force:

\(F=ma\)

Here, m is the mass of the object and a is the acceleration of the object the force is acting on.

As you can see in this simple equation, the bigger the mass, the bigger the force will need to be in order to produce the same acceleration. This equation is meant to describe the force acting in a particular direction since force is a vector quantity. This means it has both magnitude and direction. One object may have multiple forces acting on it and these forces can be added together. We can determine the overall impact of the forces (also called the net force) acting on an object by adding up all of the vectors. . This can be confusing, so let’s take a look at an example.

Here, we have a box with mass M with two forces acting on it in opposite directions. For now, we’ll assume that the box is initially at rest, and we’ll also ignore gravity and assume something is simply pulling on either side. To determine which direction the box will accelerate, we’ll need to find the total force acting on the box. Since these two forces are along the same axis, we can add them together without worrying about components of the vectors. We will denote F1 as the negative direction and F2 as the positive direction.

\(F_1+F_2=-2.0 N+3.5 N=1.5 N\)

The net or total force is 1.5 N in the positive direction (to the right), so the box will accelerate in that direction as if only a 1.5 N force in the positive direction were acting on it.

Let’s consider a slightly more difficult (and more realistic) problem.

In this problem, a man is pulling a wagon at a 45° angle from the ground. We have the force of gravity acting downward with a force of 40 N and the force of 50 N from the pull. If we want to determine the net force here in the direction of acceleration, we should set up the problem on an x–y coordinate system with the mass (the wagon) at the center. We would then need to break up F₂ into its x and y components. As you can see, F₁ only has a y component and won’t require the same treatment.

In order to break up vector components, we use trigonometry based on the concept of trigonometric ratios of triangles.

This is how we find the x and y components of the F₂.

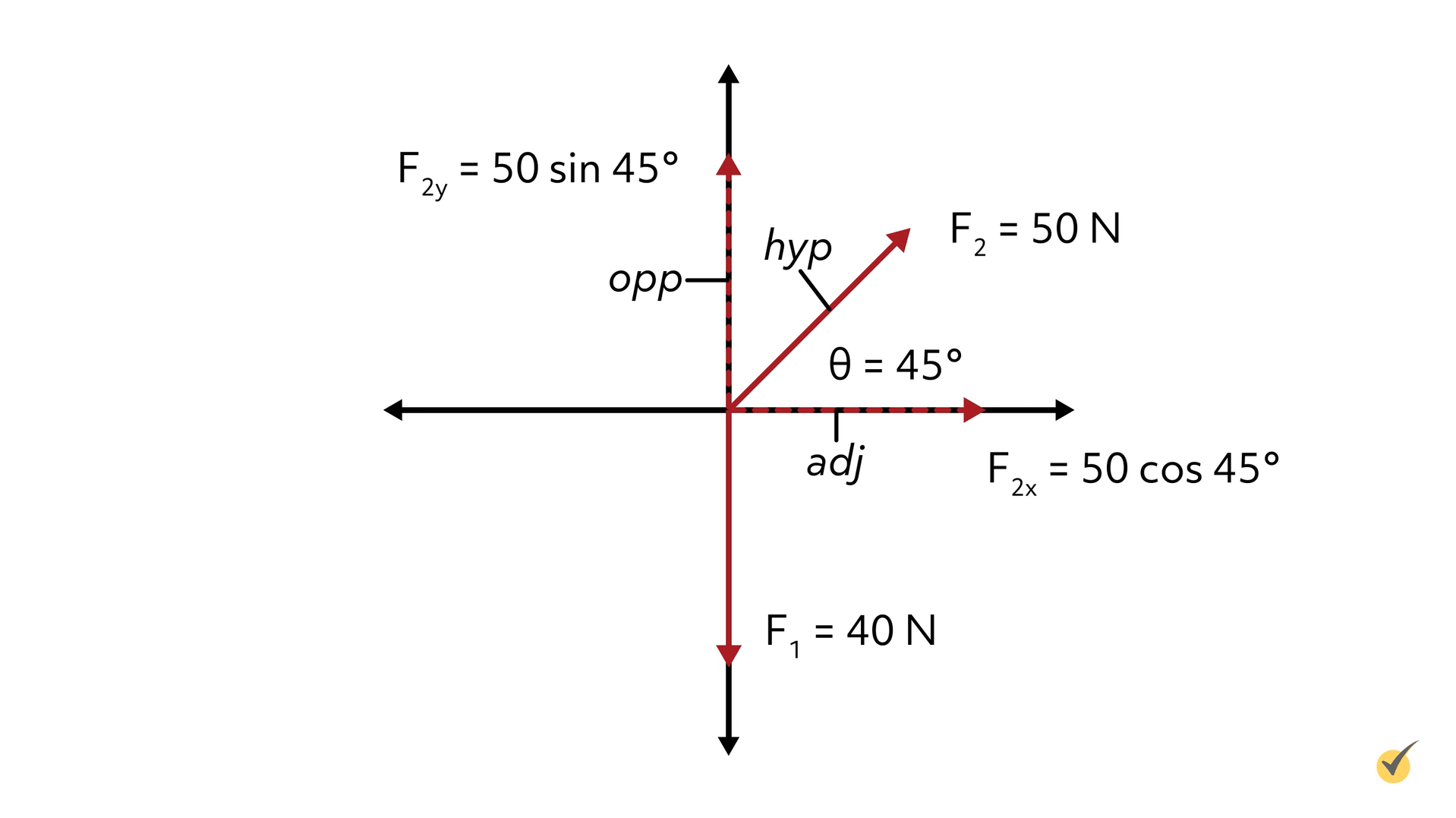
We are given that 50 is the value of the hypotenuse, so we can find the components using cos and sin and multiplying by the hypotenuse. We do not need to use the Pythagorean theorem here at all, we only use the ratios and then multiply both sides by the hypotenuse. “Opposite” is the y component (F_2y) and “adjacent” is the x component (F_2x). We say opposite because that side is opposite the known angle and the adjacent side is touching it. Using the values given in our problem, we get about 35 N for both components:

\(F_{2x}=50(cos 45°)≈35 N\)
\(F_{2y}=50 (sin 45°)≈35 N\)

In this case, the magnitude of the components is the same because of the 45° angle. The wagon is on the ground and whenever an object is on the ground, that means there is a normal force. In other words, there is an upward force that the ground exerts on the wagon. This is why the wagon does not move in the y direction.

Putting everything together, we get:

• Forces in the x direction: 35 N
• Forces in the y direction: \(F_N-40 N+35 N=0\)

This shows us that the wagon is moving in the positive x direction from the pull of the man. The main thing to remember about forces is that you have to take all forces acting on an object into account, remembering that forces or components in opposite directions will fully or at least partially cancel each other out, while forces or components in the same direction add together. Just think about a game of tug-of-war. If you add more people on your side, your side is able to pull harder, while the opposite is true if the other side adds more people.

Now that we have learned about how to deal with forces, let’s check our knowledge with a couple of questions.

Review Question

1. You pick up a ball with a mass of 2.0 kg. How much force must you exert upward in order to overcome the pull of gravity?

1. 19.6 N
2. 4.9 N
3. 2.0 N
4. Need more information

2. Assuming all the forces in this diagram have equal magnitudes, which direction will the net force be in (this will be the direction the object moves)?

1. Up
2. Left
3. Down
4. Right

That’s all for this review! Thanks for watching, and happy studying!