Displacement in Physics

Transcript

Today, we’re going to look at what displacement is and how it relates to “total distance”.

Displacement Formula

Displacement happens when an object moves from one location to another. The general equation for displacement is:

\(\text{displacement} = \text{final position} – \text{initial position}\)

The most important part of displacement is noting that the path we take to get from one location to another does not matter. We only need to know where we started and where we ended up. Sometimes we call displacement an “as the crow flies” measurement, meaning a crow flies directly from one place to another using the shortest path possible. Similarly, displacement tells us the shortest distance from an initial location to a final location.

Displacement Example 1

Let’s look at skiing for example. A group of skiers will start at the top of the mountain. One skier really likes adventure, so she zigs and zags all around the mountain as she skis down the hill. This skier loves going as fast as possible, so he zips straight down from the ski lift to the bottom. This last skier sees that the slope is a lot steeper than she thought, so she takes the lift back down. We consider the top of the mountain the initial position and the bottom of the mountain the final position. All the skiers took different paths to get from the top of the mountain to the bottom of the mountain, but their displacement is exactly the same.

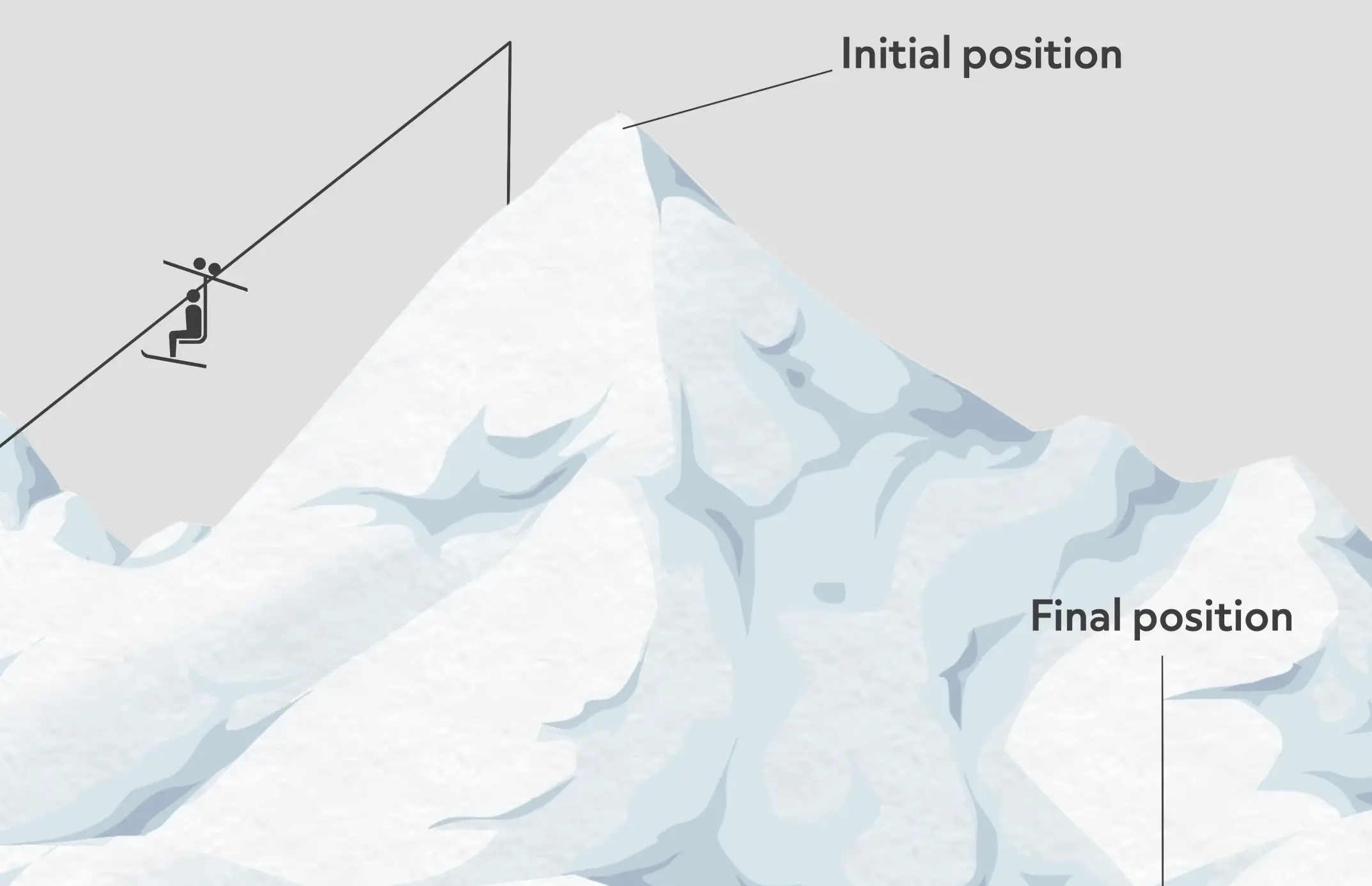
Displacement Example 2

Another example is Jackie Joyner-Kersee’s world record long jump. Her initial position is a line she runs to and begins her jump from. Her final position was 7.40 meters away. The jump was a straight line across the ground, but she jumped over the ground in an arc. The world record doesn’t care about how high off the ground she was; it only considers her starting and final positions.

Determining Total Distance

But what if you want total distance? A car’s odometer tells us how far the car has traveled in total. It is a measure of displacement that takes the path into account by breaking the path into tiny pieces. For example, it’s two miles to grandma’s house if we went directly through the forest on a straight path. But our car’s odometer says we traveled three miles. We have to go over a bridge and along a winding road, so the distance we’ve traveled is three miles, even though our displacement is less.

Direction of Displacement

Sometimes we want to specify not just the total displacement, but also the direction of the displacement. These two pieces of information, when used together, form what is called a vector. A vector gives us the magnitude and a direction. The magnitude is the total displacement and the direction is an arrow pointing from the initial location to the final location.

A common example is giving a friend directions from their house to yours. Consider these directions: “Go left, then go right, then you will be at my house.” We can’t use these directions, because they don’t include a total displacement! But what if your friend said, “Go three blocks, then go four blocks, then go seven blocks.”? That’s not enough information either! There are no directions to turn! We need vectors; a direction to turn and how long to travel in that direction.

Review

Before we go, let’s wrap up with a review question:

In flyball, dogs take turns running down a track, grabbing a ball, then running back to the start, like a relay race. If the track is 100 meters long, what is the total displacement of the four-dog team?

400 meters
800 meters
0 meters
It depends on the breed of the dogs

Thanks for watching, and happy studying!

Return to Physics Videos