What are Angles?
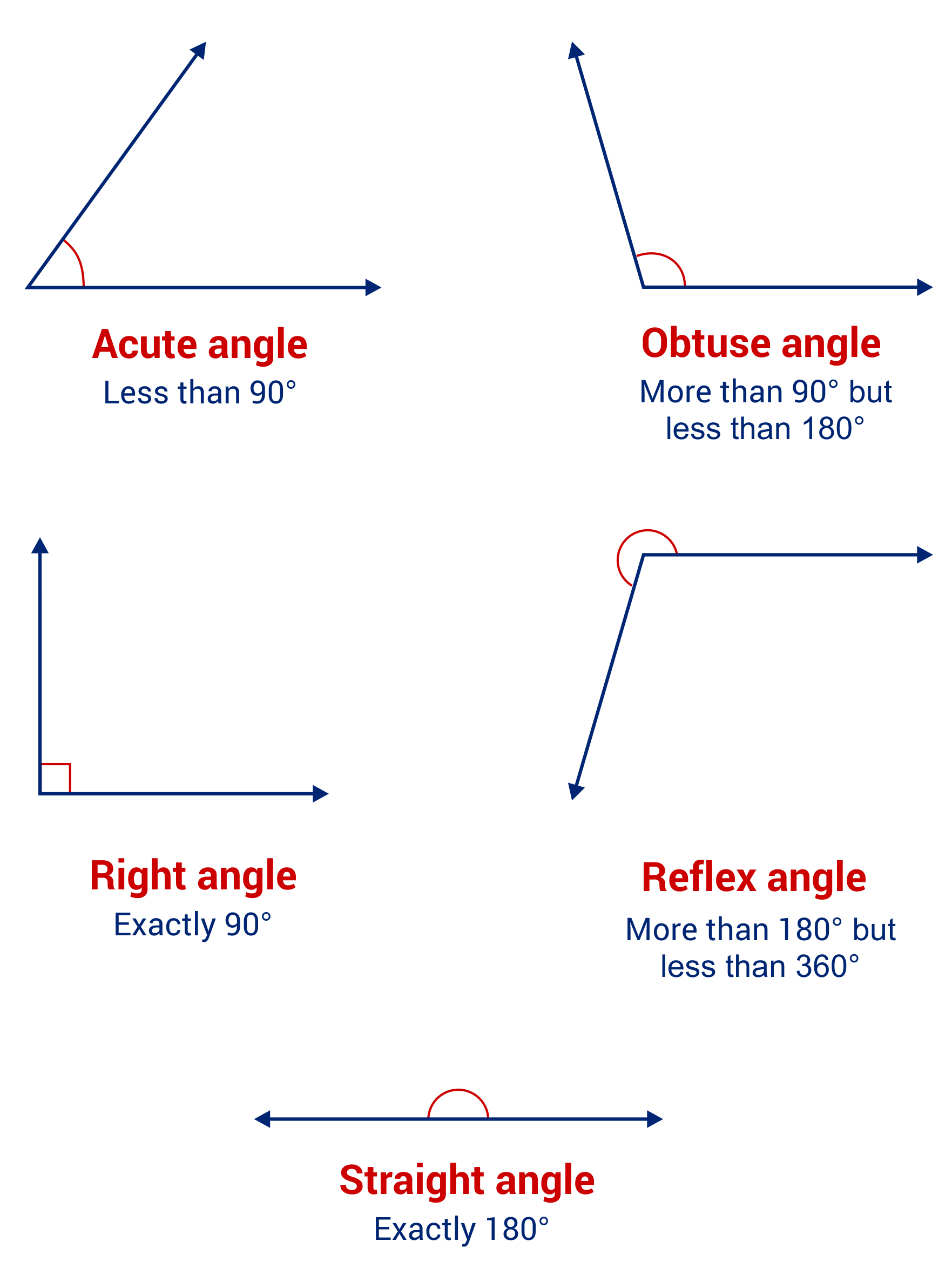
We use degrees as units of measurement for angles, and precisely determining how wide or narrow they are. The small circle symbol “°” is used following a number to denote that degrees are being represented. Note the following classifications:
- An acute angle is between 0-90°
- A right angle is 90°
- An obtuse angle is between 90-180°
- A straight angle is 180°
- A reflex angle is between 180-360°
- A full circle contains 360°, and a 360° angle is called a complete angle
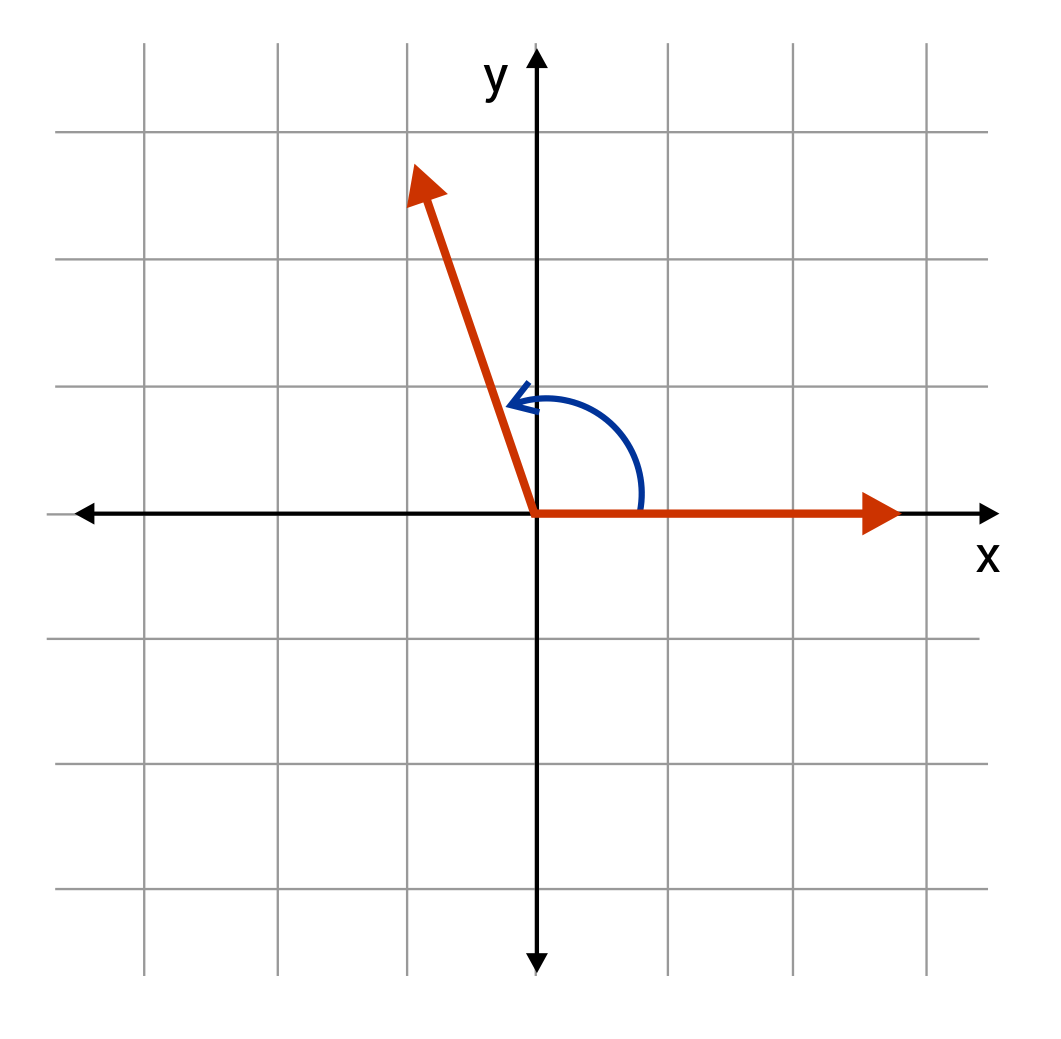
Note that when we use angles on the Cartesian plane, the angles always begin on the positive \(x\)-axis and open in the counterclockwise direction. For this reason, the positive \(x\)-axis is referred to as 0° in polar coordinates, which we will address later.
Radians are simply another way of measuring angles. Rather than divide a circle into 360 tiny “slices,” radians offer a clever and intuitive way to measure angles. One radian is the angle at which the radius of the circle equals the length of the arc of the curve drawn with that angle.
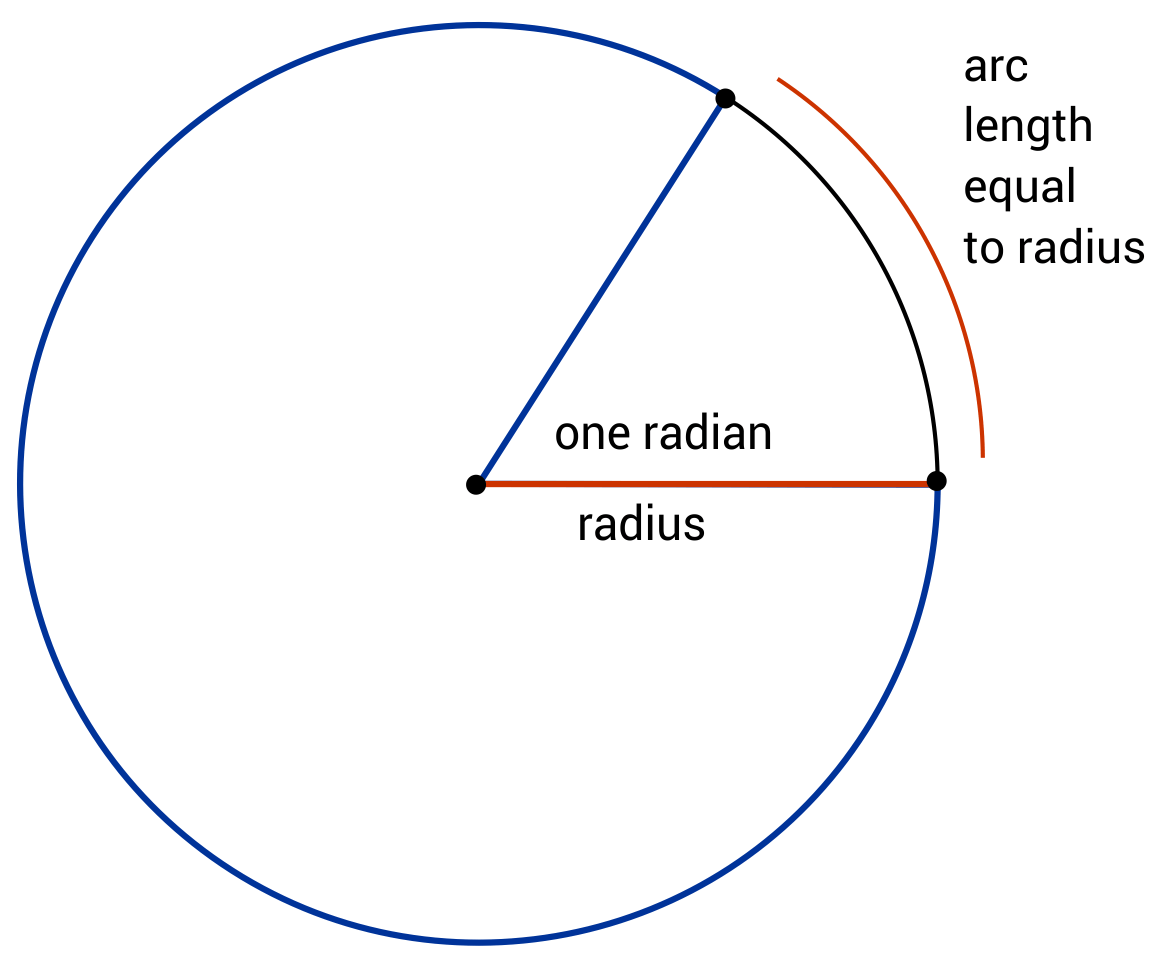
Notice from the illustration above that the angle of one radian is almost one sixth of the circle. So how many radians are in a full revolution then? Recall the relationship between the radius of a circle and its circumference.
\(C = 2r\)
The circumference of a circle is equal to \(pi\) times its diameter, or equivalently, times twice its radius. And since the length of the circle’s radius is equal to one radian, the circumference is equal to \(2pi\) radians. In other words, one full revolution contains \(2pi\) radians.
We most commonly use radians when dealing with the trigonometric functions (sin, cos, tan, csc, sec, and cot).
Degrees to Radians
How do we convert from degrees to radians? We need a way to convert our number of degrees into some number of radians, so we will derive a conversion factor with which to do so. Remember that there are 360° in a circle, and that there are \(2pi\) radians in a circle. This means that \(360text{ degrees}=2pitext{ radians}\).
We can divide both sides by 2 to simplify this equation to \(180text{ degrees}=pitext{ radians}\).
Finally, we are going to divide both sides by 180 degrees.
\(frac{180text{ degrees}}{180text{ degrees}}=frac{πtext{ radians}}{180text{ degrees}}\)
\(1=frac{πtext{ radians}}{180text{ degrees}}\)
What exactly have we ended up with here? Because \(frac{πtext{ radians}}{180text{ degrees}}\) is equal to 1, we can multiply our number of degrees by this conversion factor without changing their value. The “degrees” units will cancel with each other, leaving us with radians once we simplify the numerical values!
Our constant for converting degrees to radians is\(mathbf{frac{πtext{ radians}}{180text{ degrees}}}\)
Conversion Example
Let’s work an example by converting 120° to radians. To begin, we multiply 120 degrees by our conversion factor, \(frac{πtext{ radians}}{180text{ degrees}}\).
\(120text{ degrees}×frac{πtext{ radians}}{180text{ degrees}}=frac{120pi}{180}text{ radians}=frac{2}{3}pitext{ radians}\)
How do we convert from radians to degrees? It is very straightforward to derive the conversion factor for radians to degrees.
\(360text{ degrees}=2pi text{ radians}\)
\(180text{ degrees}=pitext{ radians}\)
This time, we want the radians unit to end up in the denominator so that when we multiply our number of radians by the conversion factor, the “radians” units cancel each other and leave us with only degrees.
\(frac{180 degrees}{π radians}=frac{πtext{ radians}}{πtext{ radians}}\)
\(frac{180text{ degrees}}{πtext{ radians}}=1\)
Just like before, we can now use this conversion factor to take a number of radians and change them into degrees.
Our constant for converting radians to degrees is \(mathbf{frac{180text{ degrees}}{πtext{ radians}}}\).
As an example, let’s now convert \(frac{5π}{4}\) radians to degrees. We multiply our \(frac{5π}{4}\) radians by the conversion factor \(frac{180text{ degrees}}{πtext{ radians}}\) to eliminate the unit “radians”. From there, the π’s in the numerator and denominator cancel each other, and a little arithmetic leaves us with our solution, 225°.
\(frac{5π}{4}text{ radians}× frac{180text{ degrees}}{πtext{ radians}}=frac{5πtimes180}{4timesπ}text{ degrees}=225text{ degrees}\)
What are polar coordinates?
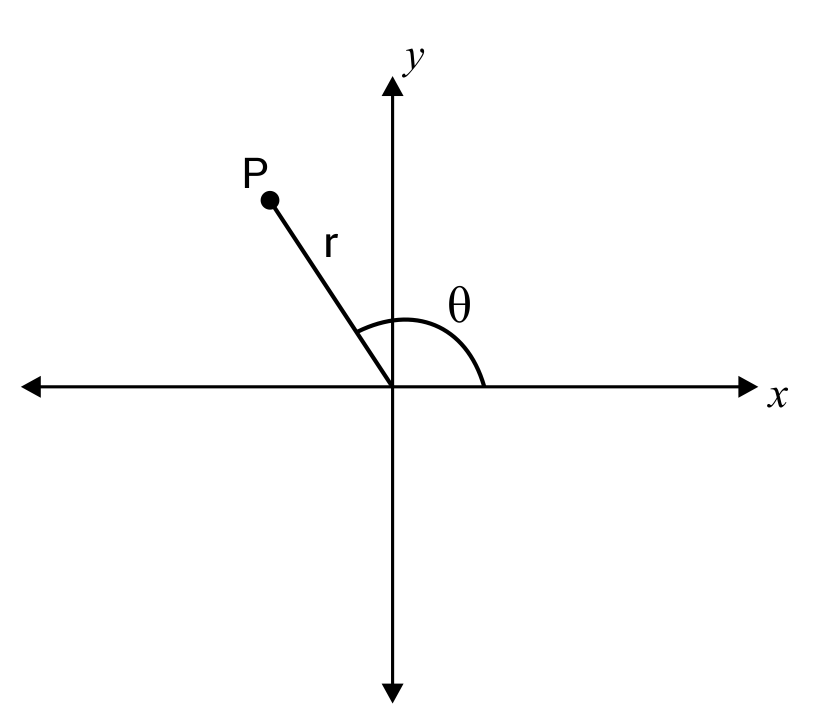
In the same way that we usually use ordered pairs \((x,y)\) to describe points on the Cartesian plane, we can also describe points using the polar coordinates \((r,θ)\). The lowercase r is a parameter specifying how far away the point is from the origin, and the Greek letter (pronounced “they-ta”) specifies at which angle the point is from the positive x-axis. Usually, we don’t need to use polar coordinates until we get into content from Calculus II, but it can be helpful to see that this is one application for which we use radians in mathematics.
Using the Correct Mode in Your Calculator
Scientific calculators are programmed to perform many different functions, including working with both degrees and radians. However, they can only process in terms of one or the other at a single time. If you are dealing with degrees, it is important to make sure that your calculator is in “degrees” mode first.
- For Texas Instruments calculators, press the [MODE] button, then use the arrow keys to highlight DEGREE, and press [ENTER].
- For Casio calculators, press [SHIFT] and then [MODE] to access Setup, then press 3 to begin working in degrees.
To put your calculator in “radians” mode, follow these similar steps.
- For Texas Instruments, press the [MODE] button, then use the arrow keys to highlight RAD, and press [ENTER].
- For Casio, press [SHIFT] then [MODE], and finally press 4 to begin working in radians.
Degrees and Radians Sample Questions
Here are a few sample questions going over degrees and radians.
Convert \(\pi\) radians to degrees.
\(\pi\text{ radians}\times\frac{180\text{ degrees}}{\pi\text{ radians}}=\frac{180\pi}{\pi}\text{ degrees}=180°\)
Convert 30° to radians.
\(30\text{ degrees}=\frac{\pi\text{ radians}}{180\text{ degrees}}=\frac{30 \pi}{180}\text{ radians}=\frac{1}{6} \pi\text{ radians}\)
Convert \(\frac{3 \pi}{2}\) radians to degrees.
\(\frac{3 \pi}{2}\text{ radians}\times\frac{180\text{ degrees}}{\pi\text{ radians}}=\frac{3 \pi\times180}{2 \pi}\text{ degrees}=270\text{ degrees}\)
Convert 45° to radians.
\(45\text{ degrees}\times\frac{\pi\text{ radians}}{180\text{ degrees}}=\frac{45\pi}{180}\text{ radians}=\frac{1}{4}\pi\text{ radians}\)
Determine how the angle \(\frac{7}{8}\pi\) radians is classified.
We can determine this in two ways. First, we can convert \(\frac{7}{8}\pi\) radians to degrees and then refer to the angle guide presented earlier. This is equivalent to 157.5°, and since that value is between 90-180°, we see that it is obtuse.
\(\frac{7}{8}π\text{ radians}\times\frac{180\text{ degrees}}{π\text{ radians}}=\frac{7π×180}{8\pi}\text{ degrees}=157.5°\)
We can also determine that the angle is obtuse without converting to degrees. Remember that since \(2\pi= 360\text{ degrees}\), then we can easily determine by division that \(\pi=180\text{ degrees}\), and \(2\pi=90\text{ degrees}\). Since \(\frac{7}{8}\pi\) is clearly between \(\frac{\pi}{2}\) and \(\pi\), we see that it is an obtuse angle.
