The conversion of area measurements is the process of changing between different units of measurement for the same quantity.
For example, if a garden has an area of 1 square yard, this area can be converted to an equivalent amount of feet. Since 1 yard is equal to 3 feet, the length and the width of the garden (in feet) is 3 feet by 3 feet. Therefore, the area of the garden \((\text{length}\times \text{width})\) is 9 square feet.
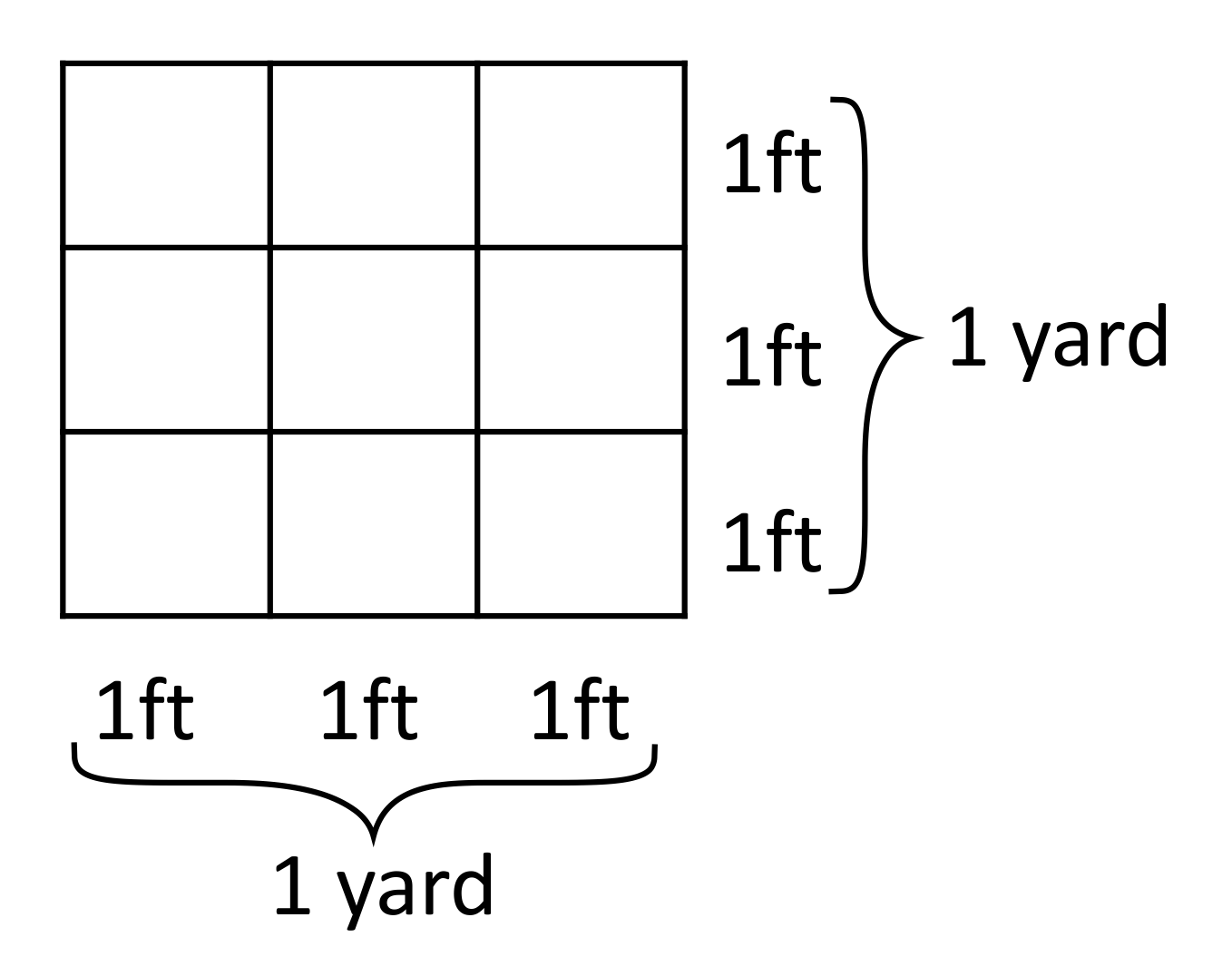
Converting between Two Area Units
To convert between two area units, you must first identify the two units of measurement in the problem. For instance, if you need to convert from meters to centimeters, then the units of measurement are meters and centimeters.
Next, find the measurement equivalent of the first unit to the second.
Using the example of converting from meters to centimeters, identify how many centimeters are in one meter:
\(100\text{ cm}=1\text{ m}\)
From here, use the measurement equivalent to solve. Using the example of converting from meters to centimeters, we will find how many square centimeters are in 5 square meters.
We can rewrite “5 square meters” as \(5\text{ }m^2\), or \(5\times m\times m\). Recall that 100 centimeters is equal to 1 meter (m).
Using the expression 5 mm, substitute 100 cm into the formula for the variable \(m\).
\(5\times 100\text{ cm}\times 100\text{ cm}\)
Next, multiply from left to right.
\(5\times100\text{ cm}=500\text{ cm}\)
Since \(5\times100\text{ cm}=500\text{ cm}\), rewrite the expression using \(500\text{ cm}\).
\(500\text{ cm}\times 100\text{ cm}\)
Finally, multiply to solve.
Because \(500\text{ cm}\times 100\text{ cm}=50{,}000\text{ cm}^2\), \(5\text{ m}^2=50{,}000\text{ cm}^2\).
Area Conversions vs. Length Conversions
Converting an area measurement is different from converting a length measurement. For instance, converting 5 meters to centimeters is as simple as multiplying \(5\) by \(100\), since there are \(100\) centimeters in \(1\) meter.
Area measurement conversions involve multiplying the given area by the unit equivalent two times. In the example above, which converts \(5\) square meters into square centimeters, multiply \(5\) times \(100\) times \(100\) again.
Length is measured in units, and area is measured in square units \((\text{unit}\times \text{unit}=\text{unit}^2)\). For this reason, the unit equivalent is multiplied twice in area conversions.
Example 1
Fill in the blank: \(2\text{ cm}^2=\) ___ \(\text{ mm}^2 (1\text{ cm}=10\text{ mm})\)
1. First, we can say that \(2\text{ cm}^2\) is equal to \(2\times \text{ cm}\times \text{ cm}\).
\(2\text{ cm}^2=2\times \text{ cm}\times \text{ cm}\)
2. Since \(1\text{ cm}=10\text{ mm}\), substitute \(10\text{ mm}\) into the expression for \(\text{cm}\) and solve.
\(2\times10\text{ mm}\times10\text{ mm}\)
3. Next, multiply from left to right. Since \(2\times10\text{ mm}=20\text{ mm}\), rewrite the expression using \(20\text{ mm}\).
\(20\text{ mm}\times 10\text{ mm}\)
4. Finally, multiply to solve.
\(20\text{ mm}\times 10\text{ mm}=200\text{ mm}^2\)
\(2\text{ cm}^2=200\text{ mm}^2\)
Example 2
Fill in the blank: \(6\text{ ft}^2=\)___\(\text{ in}^2 (1\text{ ft}=12\text{ in})\)
1. First, we can say that \(6\text{ ft}^2\) is equal to \(6\times \text{ft}\times \text{ft}\).
\(6\text{ ft}^2=6\times \text{ft}\times \text{ft}\)
2. Since \(1\text{ ft}=12\text{ in}\), substitute \(12\text{ in}\) into the expression for \(\text{ft}\) and solve.
\(6\times12\text{ in}\times12\text{ in}\)
3. Next, multiply from left to right. Since \(6\times12\text{ in}=72\text{ in}\), rewrite the expression using \(72\text{ in}\).
\(72\text{ in}\times 12\text{ in}\)
4. Finally, multiply to solve.
\(72\text{ in}\times12\text{ in}=864\text{ in}^2\)
\(6\text{ ft}^2=864\text{ in}^2\)
Example 3
Fill in the blank: \(640{,}000\text{ m}^2=\)___\(\text{km}^2 (1\text{ m}=0.001\text{ km})\)
1. First, we can say that \(640{,}000\text{ m}^2\) is equal to \(640{,}000\text {mm}\).
\(640{,}000\text{ m}^2=640{,}000\text{ mm}\)
2. Since \(1\text{ m}=0.001\text{ km}\), substitute \(0.001\text{ km}\) into the expression for \(m\) and solve.
\(640{,}000\times0.001\text{ km}\times0.001\text{ km}\)
3. Next, multiply from left to right. Since \(640{,}000\times0.001\text{ km}\), rewrite the expression using \(640\text{ km}\).
\(640\text{ km}\times0.001\text{ km}\)
4. Finally, multiply to solve.
\(640\text{ km}\times0.001\text{ km}=0.64\text{ km}^2\)
\(640{,}000\text{ m}^2=0.64\text{ km}^2\)
Converting Area Measurement Sample Questions
Here are a few sample questions going over converting area measurements.
Convert between the following area measurements:
\(64\text{ m}^2=\)___ \(\text{cm}^2\)
\((1\text{ m}=100\text{ cm})\)
1. First, we can say that \(64\text{ m}^2\) is equal to \(64\text{ mm}\).
\(64\text{ m}^2=64\text{ mm}\)
2. Since \(1\text{ m}=100\text{ cm}\), substitute \(100\text{ cm}\) into the expression for \(m\) and solve.
\(64\times100\text{ cm}\times100\text{ cm}\)
3. Next, multiply from left to right. Since \(64\times100\text{ cm}=6{,}400\text{ cm}\), rewrite the expression using \(6{,}400\text{ cm}\).
\(6{,}400\text{ cm}\times100\text{ cm}\)
4. Finally, multiply to solve.
\(6{,}400\text{ cm}\times 100\text{ cm}=640{,}000\text{ cm}^2\)
Therefore, the correct answer is D.
Nick is building a patio in his backyard with an area of \(5{,}184\) square inches. To figure out how much concrete he needs to buy, Nick needs to know the area of the patio in square feet. How many square feet are equal to \(5{,}184\) square inches? Round your answer to the nearest whole number. (\((1\text{ in}=0.083\text{ ft})\).)
1. First, we can say that \(5{,}184\text{ in}^2\) is equal to \(5{,}184\times \text{in}\times \text{in}\).
\(5{,}184\text{ in}^2=5{,}184\times \text{in}\times \text{in}\)
2. Since \(1\text{ in}=0.08\overline{3}\text{ ft}\), substitute \(0.08\overline{3}\text{ ft}\) into the expression for in and solve.
\(5{,}184\times0.08\overline{3}\text{ ft}\times0.08\overline{3}\text{ ft}\)
3. Next, multiply from left to right. Since \(5{,}148\times0.08\overline{3}\text{ ft}\approx 429\text{ ft}\), rewrite the expression using \(429\text{ ft}\).
\(429\text{ ft}\times 0.08\overline{3}\text{ ft}\)
4. Finally, multiply to solve. \(429\text{ ft}\times 0.08\overline{3}\text{ ft}\approx 35.75\text{ ft}^2\). \(5{,}184\) square inches (rounded to the nearest whole number) is \(36\) square feet.
\(35.75\text{ ft}^2\approx 36\text{ ft}^2\)
Therefore, the correct answer is D.
Convert between the following area measurements:
\(500{,}000\text{ mm}^2=\)___ \(\text{m}^2\)
\((1\text{ mm}=0.001\text{ m})\)
1. First, we can say that \(500{,}000\text{ mm}^2\) is equal to \(500{,}000\times \text{ mm}\times \text{ mm}\).
\(500{,}000\text{ mm}^2=500{,}000\times \text{ mm}\times \text{ mm}\)
2. Since \(1\text{ mm}=0.001\text{ m}\), substitute \(0.001\text{ m}\) into the expression for \(\text{mm}\) and solve.
\(500{,}000\times 0.001\text{ m}\times0.001\text{ m}\)
3. Next, multiply from left to right. Since \(500{,}000\times0.001\text{ m}=500\text{ m}\), rewrite the expression using \(500\text{ m}\).
\(500\text{ m}\times0.001\text{ m}\)
4. Finally, multiply to solve.
\(500\text{ m}\times0.001\text{ m}=0.5\text{ m}^2\)
Therefore, the correct answer is C.
Jamal’s garden has an area of \(120\) square yards. To figure out how much soil he needs to purchase, Jamal needs to know the area of his garden in square feet. What is the area of Jamal’s garden in square feet?
\((1\text{ yd}=3\text{ ft})\)
1. First, we can say that \(120\text{ yd}^2\) is equal to 120\times \text{yd}\times \text{yd}[/latex].
\(120\text{ yd}^2=120\times \text{yd}\times \text{yd}\)
2. Since \(1\text{ yd}=3\text{ ft}\), substitute \(3\text{ ft}\) into the expression for \(\text{yd}\) and solve.
\(120\times3\text{ ft}\times3\text{ ft}\)
3. Next, multiply from left to right. Since \(120\times3\text{ ft}=360\text{ ft}\), rewrite the expression using \(360\text{ ft}\).
\(360\text{ ft}\times3\text{ ft}\)
Finally, multiply to solve.
\(360\text{ ft}\times3\text{ ft}=1{,}080\text{ ft}^2\)
Therefore, the correct answer is A.
Convert between the following area measurements:
\(48\text{ yd}^2=\)___ \(\text{in}^2\)
\((1\text{ yd}=36\text{ in})\)
1. First, we can say that \(48\text{ yd}^2\) is equal to \(48\times \text{yd}\times \text{yd}\).
\(48\text{ yd}^2=48\times \text{yd}\times \text{yd}\)
2. Since \(1\text{ yd}=36\text{ in}\), substitute \(36\text{ in}\) into the expression for \(\text{yd}\) and solve.
\(48\times36\text{ in}\times36\text{ in}\)
3. Next, multiply from left to right. Since \(48\times36\text{ in}=1{,}728\text{ in}\), rewrite the expression using \(1{,}728\text{ in}\).
\(1{,}728\text{ in}\times36\text{ in}\)
4. Finally, multiply to solve.
\(1{,}728\text{ in}\times36\text{ in}=62{,}208\text{ in}^2\)
Therefore, the correct answer is B.
