How To Divide a Polynomial by a Monomial
Remember that a polynomial is an algebraic expression with two or more terms, and that a monomial is an algebraic expression with only one term. For example, the expression \(\frac{6x^3+12x^2+3x}{6x}\) is a polynomial divided by a monomial. If at first glance, this looks intimidating, it can be separated into chunks as follows:
\(\frac{6x^3+12x^2+3x}{6x}=\frac{6x^3}{6x}+\frac{12x^2}{6x}+\frac{3x}{6x}\)
Once the problem is broken up like this, we simply need to divide a few monomials. For the first term, \(\frac{6x^3}{6x}\), we can cancel the 6’s on the top and bottom, and cancel one \(x\) from both the top and bottom, leaving us with \(x^2\).
\(\frac{6x^3}{6x}=\frac{6x\cdot x^2}{6x}=x^2\)
The second term can be quickly reduced when we notice that \(12\) and \(6\) share a factor of \(6\), and that \(x^2\) and \(x\) share a factor of \(x\).
\(\frac{12x^2}{6x}=\frac{6\cdot 2\cdot x\cdot x}{6\cdot x}=2x\)
For the third term, \(\frac{3x}{6x}\), both \(x\)’s cancel each other out, leaving us with \(\frac{3}{6}\), which reduces to \(\frac{1}{2}\).
\(\frac{3x}{6x}=\frac{3}{6}=\frac{1}{2}\)
Now, just put these together to form the solution:
\(\frac{6x^3+12x^2+3x}{6x}=x^2+2x+\frac{1}{2}\)
While this example deals specifically with dividing a trinomial by a monomial, the same process of breaking the fraction apart into many terms can be used any time we need to divide a polynomial by a monomial. Regardless of the number of terms in the numerator, as long as the denominator has a single term, this method can be used!
How to Use Long Division to Divide Polynomials
Whenever the denominator has more than one term, we need to use a different method of division: long division. Before going further, here is a quick review of division terminology: the value in the numerator, which goes “in the house” of our long division symbol, is called the dividend. The value in the denominator, which goes to the left of “the house,” is called the divisor. Finally, the solution, which goes on top of “the house,” is called the quotient.
Let’s work through an example of polynomial long division. Divide the polynomial \(2x^3+x^2-6x-8\) by the polynomial \(x-2\). Just like in arithmetical long division, the dividend will go “in the house” and the divisor will go to the left of “the house.”
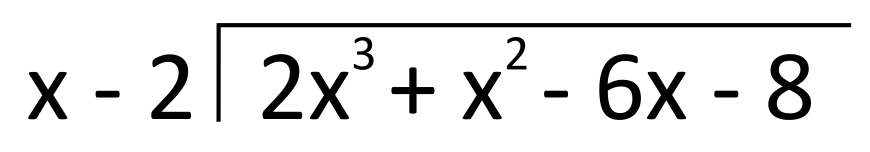
In arithmetical long division, we work from the leftmost digit of the dividend (inside the house) to the rightmost digit. With polynomial long division, we follow a similar order by starting with the first term of the dividend. For the polynomial outside the house, we also start by looking at its first term. In this example, our first step is dividing \(2x^3\) (the first term inside the house) by \(x\) (the leftmost term outside the house). We know from monomial division that \(\frac{2x^3}{x}=2x^2\), so this will be the first term of our quotient, and we will write it above the house.
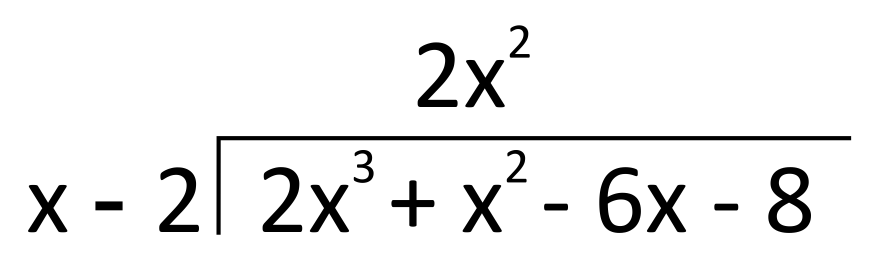
Remember that with ordinary long division, once you write something on top of the house, you then need to multiply that value by the divisor, and write the product beneath the dividend. Here we do the same! Multiply \(2x^2\) by the divisor, \(x-2\), to get \(2x^3-4x^2\). Write this below the first two terms of the dividend, and notice that the two \(2x^3\)’s will cancel each other in the next step: subtraction.
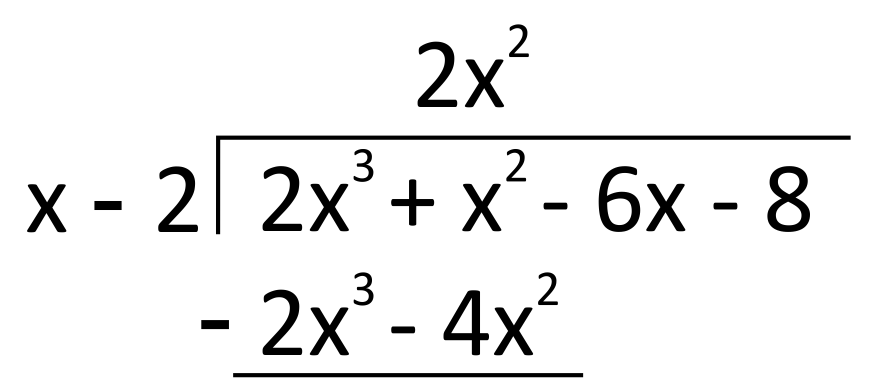
Subtract \(2x^3-4x^2\) from the two terms above it, \(2x^3+x^2\). It is very important to note with this step that because both terms are being subtracted, the sign of the second subtracted term will change. It is helpful to write parentheses around them to make an indication of this. Since \(2x^3-2x^3=0\), and \(x^2-(-4x^2)=5x^2\), we write \(0+5x^2\) down below to complete this step.
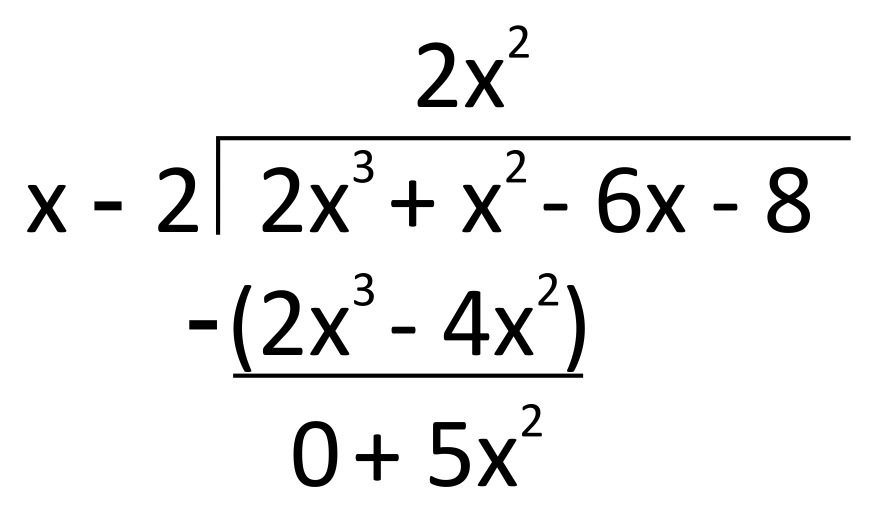
The first cycle of dividing, multiplying, and subtracting is complete. We start again by dividing what we were left with, \(5x^2\), by the first term of our divisor, \(x\). Because \(\frac{5x^2}{x}=5x\), we write \(5x\) as the second term of our quotient, above the house.
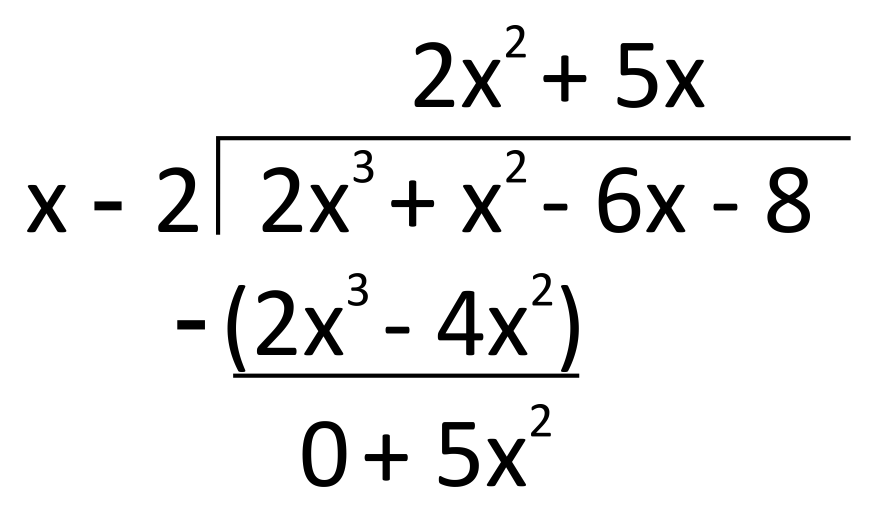
Next, we multiply this \(5x\) by the divisor: \(5x(x-2)=5x^2-10x\). Write this down below, and subtract it from the above terms of corresponding degree. We bring down the \(-6x\) term from the dividend to subtract \((5x^2-6x)-(5x^2-10x)\). Remember, the negative sign in the subtracting process will change the sign of \(10x\).
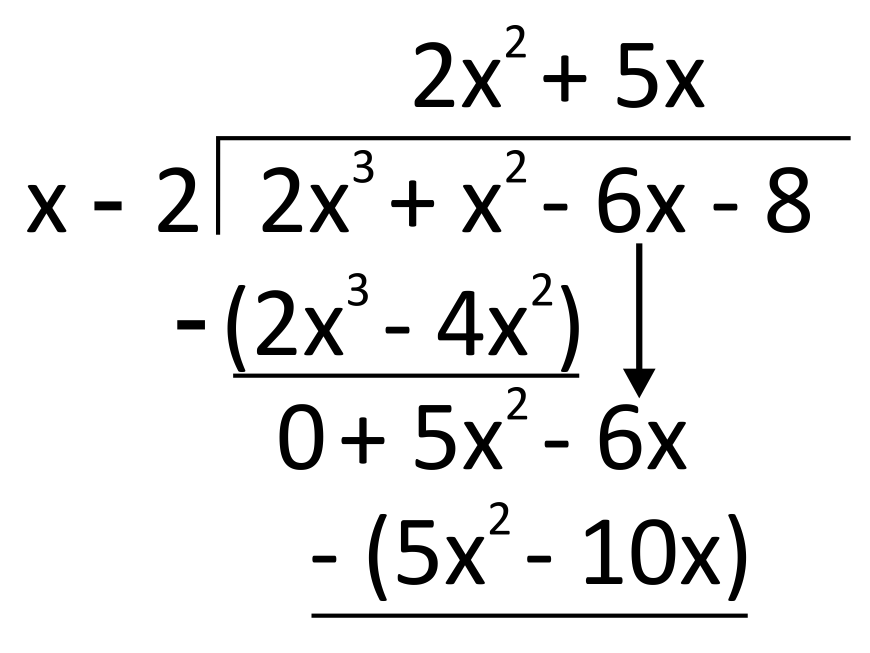
When we subtract, the \(5x^2\) terms cancel, leaving us with \(4x\).
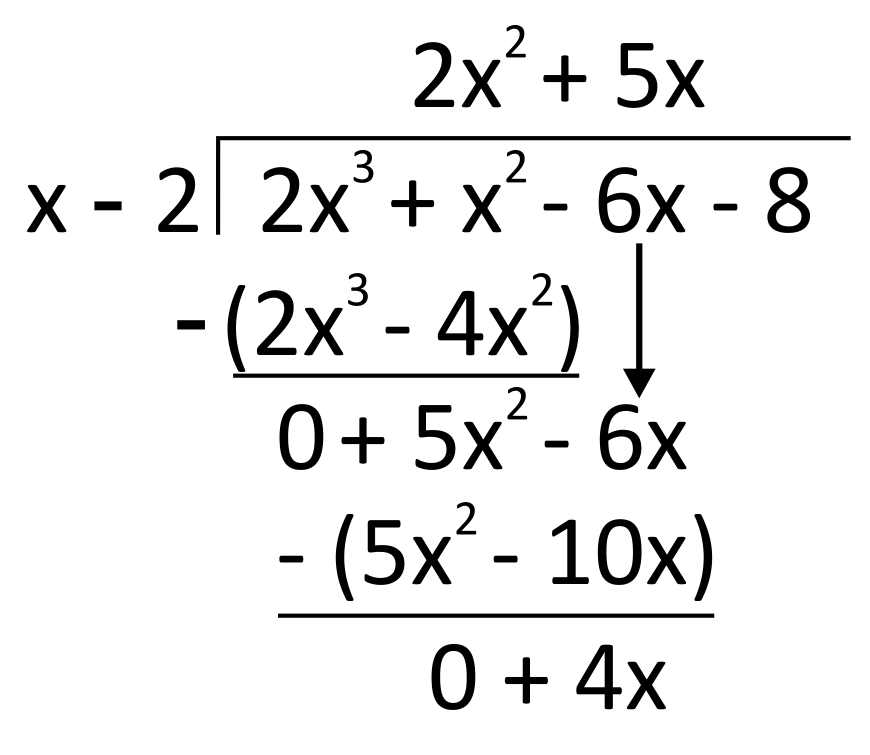
For this problem we need to complete the cycle one more time. First, divide. Because \(\frac{4x}{x}=4\), write \(4\) up on top. Then, multiply \(4\) by the divisor. \(4(x-2)=4x-8\). This goes down below.
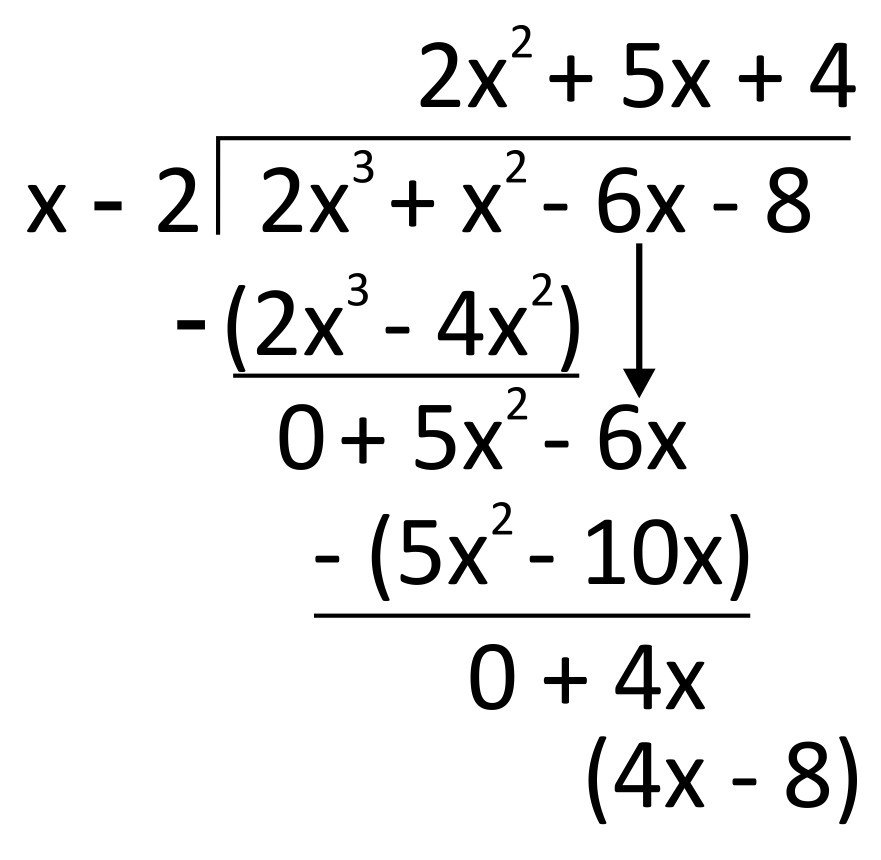
Finally, drop down the last term of the divisor, \(8\), to prepare for subtraction. \((4x-8)-(4x-8)=0\).
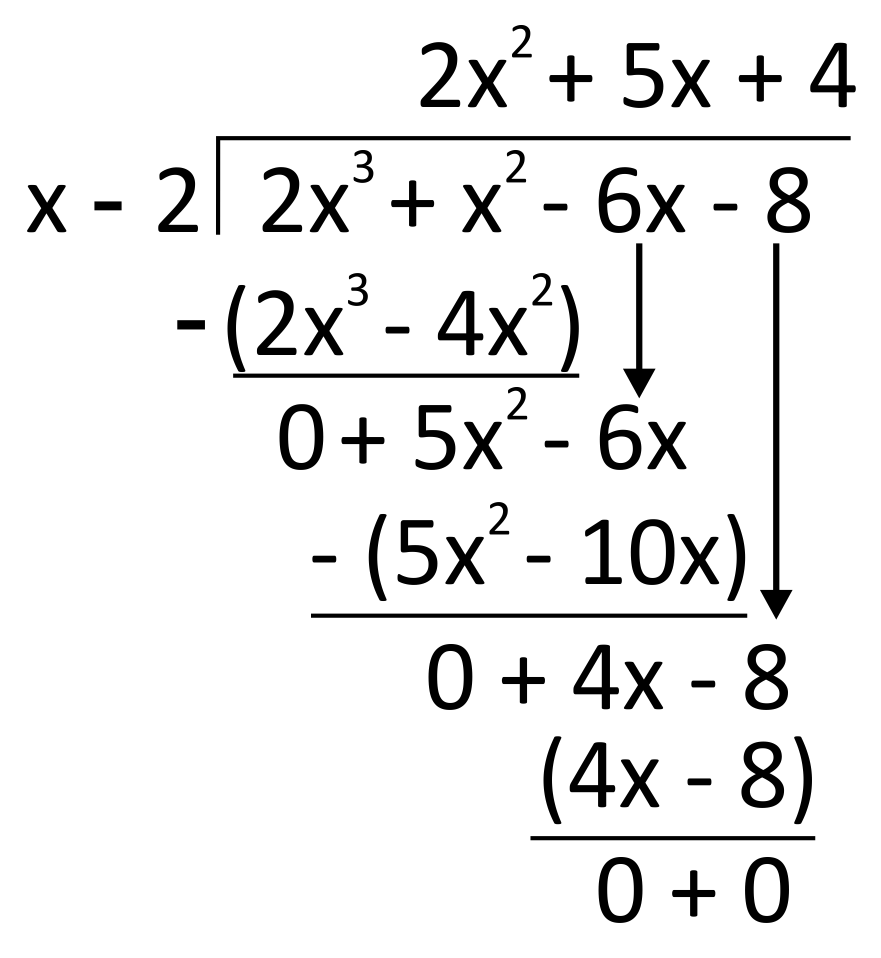
At this point, because all terms of the dividend have been divided out, we are done! Our solution is \(2x^2+5x+4\), and there is no remainder term because our final subtraction left us with \(0\). The answer can be checked by multiplying it by the divisor to get back to the dividend:
\((x-2)(2x^2+5x+4)=2x^3+5x^2+4x-4x^2-10x-8=2x^3+x^2-6x-8\)
In short, to divide polynomials, start with the term with the highest exponent in the dividend, and divide it by the term with the highest exponent of the divisor. Write this quotient above the house and multiply it by the divisor, putting this new product below the dividend. Subtract the product from the terms above it, and repeat this cycle until all terms of the dividend have been worked through.
What do you do if there is a remainder?
In some polynomial division problems, we do not end up with 0 after the final subtraction. Just like in regular long division, in these cases we have a remainder. However, unlike regular long division, we do not simply write the letter “r” off to the side with the remainder. Instead, we write the remainder in with the rest of our solution as a final term, a fraction whose numerator is the leftover from subtraction and whose denominator is the divisor.
For example, the problem below has been worked out until a positive \(2\) is left over.
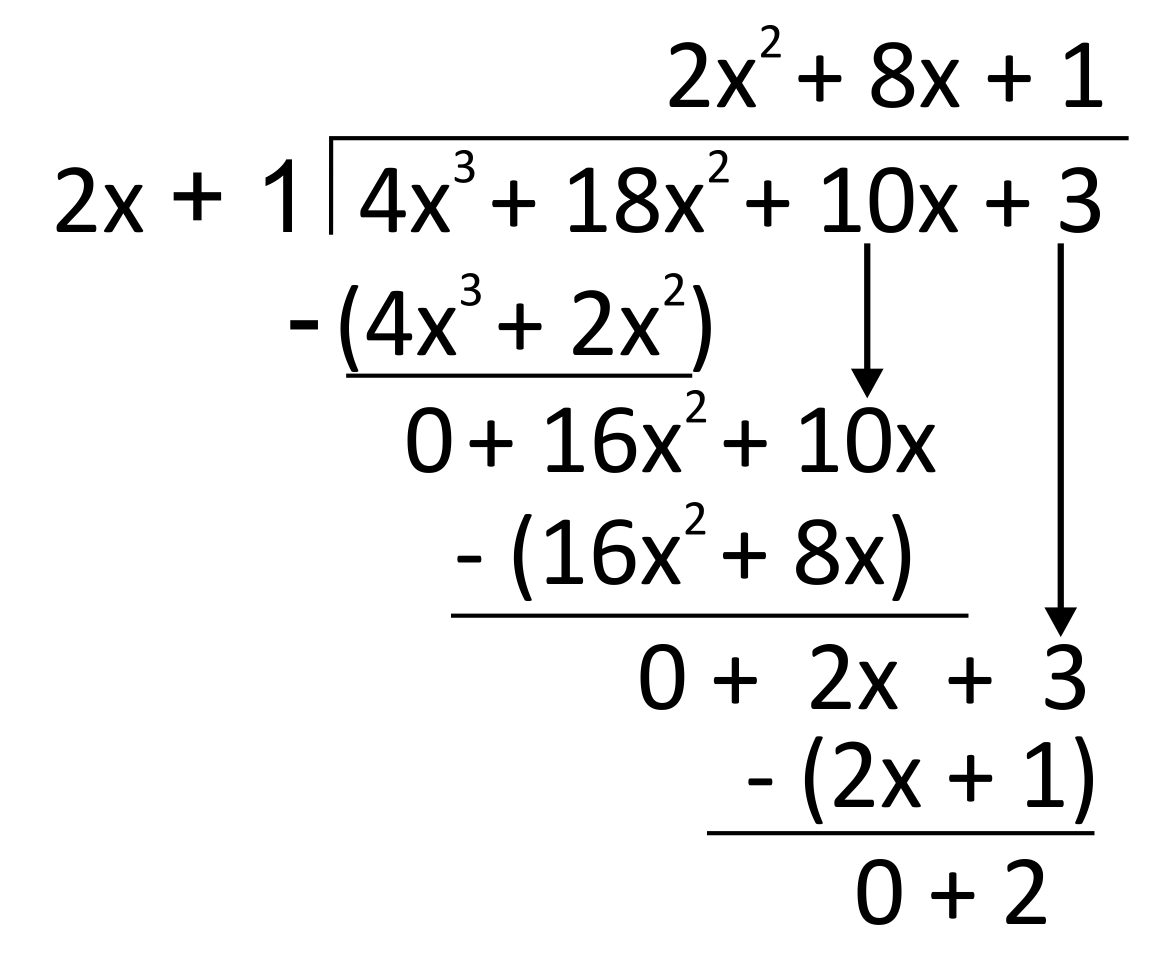
To build the remainder term, write this leftover \(2\) above the divisor, \(2x+1\), as a fraction: \(\frac{2}{2x+1}\). We then add this fraction to the part of the quotient we have written above “the house” to get the final answer: \(2x^2+8x+1+\frac{2}{2x+1}\). To check this solution, multiply it by the divisor to get back to the dividend.
\((2x+1)(2x^2+8x+1+\frac{2}{2x+1})=4x^3+16x^2+2x+\frac{4x}{2x+1}+2x^2+8x+1+\frac{2}{2x+1}\)
\(=4x^3+18x^2+10x+1+\frac{4x+2}{2x+1}\)
\(=4x^3+18x^2+10x+1+2\)
\(=4x^3+18x^2+10x+3\)
What do you do if there are missing terms?
Some polynomials have missing terms, where there are “jumps” from one exponent to another. What does that mean exactly? Look at the following polynomials and see what they have in common: \(2x^2+6\), \(4x^3+8x+2\), and \(x^5+x^2\). While the terms are listed in decreasing order of exponents, there are clearly missing terms in each polynomial. In the last one, \(x^5+x^2\), there are actually four missing terms: the fourth-power term, the third-power term, the first-power term, and the zero-power or constant term.
Whenever a polynomial has one or more missing terms, we need to write them in, each with coefficient 0, so that we can correctly follow the long division process. For example, we would adjust each of the above polynomials with 0-terms like this:
\(2x^2+6=2x^2+0x+6\)
\(4x^3+8x+2=4x^3+0x^2+8x+2\)
\(x^5+x^2=x^5+0x^4+0x^3+x^2+0x+0\)
Note that we are not concerned about adding 0-terms of exponents greater than the first term. Now, let’s work a full example of polynomial division with missing terms.
Use long division to divide \(x^3+x\) by \(x+3\).
Notice that our dividend starts with a third-power term but has no second-power term and no constant term. Our first step is to write these in with coefficients of 0. This alters our dividend to become \(x^3+0x^2+x+0\). The divisor, \(x+3\), has no missing terms, so it has no need for zero-coefficient terms.
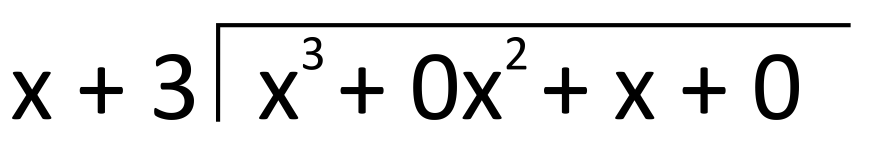
Moving through the dividend one term at a time, we first divide \(x^3\) by \(x\), the first term of the divisor. This gives us \(x^2\), which we write on top of “the house.”
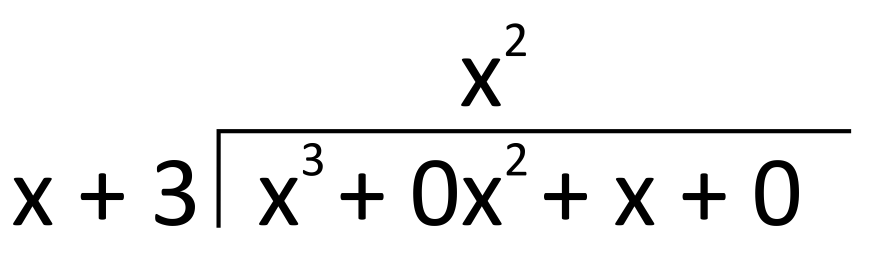
Multiplying the divisor by \(x^2\), we then write \(x^3+3x^2\) below the first two terms of the dividend, and subtract.
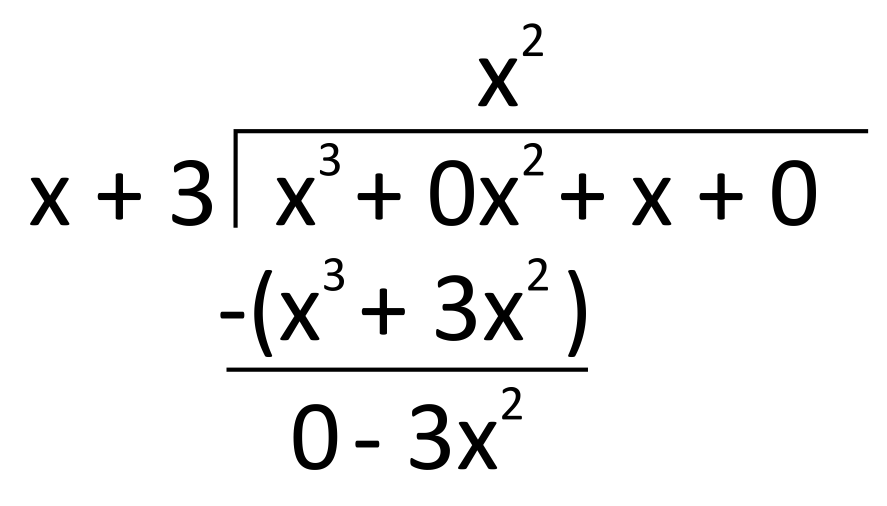
Our first cycle leaves us with \(-3x^2\), so we continue the long division by dividing this by the first term of the divisor, \(x\). This gives us \(-3x\), which we write as the second term of our quotient. Next, multiply \(-3x\) by \(x+3\) and write the product, \(-3x^2-9x\), down below.
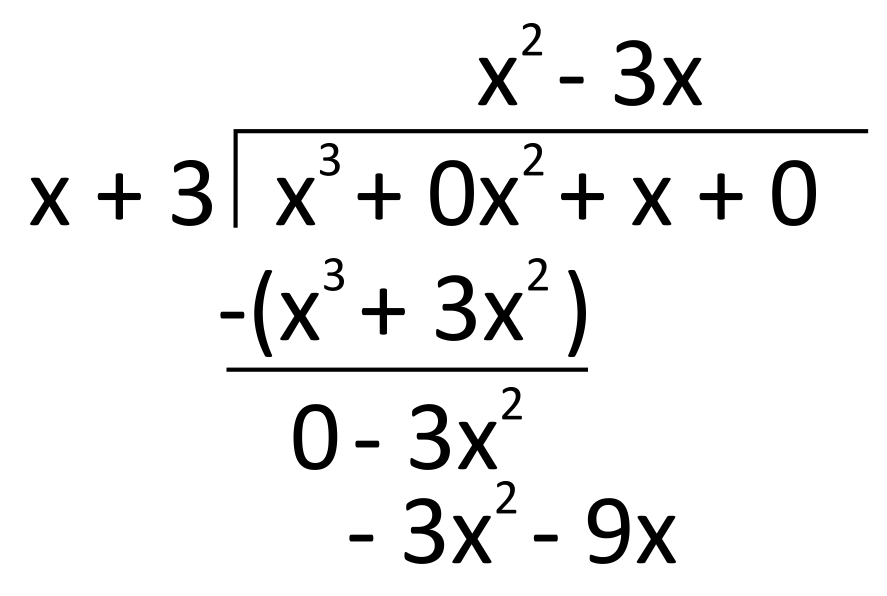
To make the next subtraction, we drop down the next term of the dividend, \(x\), right above the \(-9x\), and draw parentheses around \(-3x^2-9x\) so that we do not lose track of the changing signs.
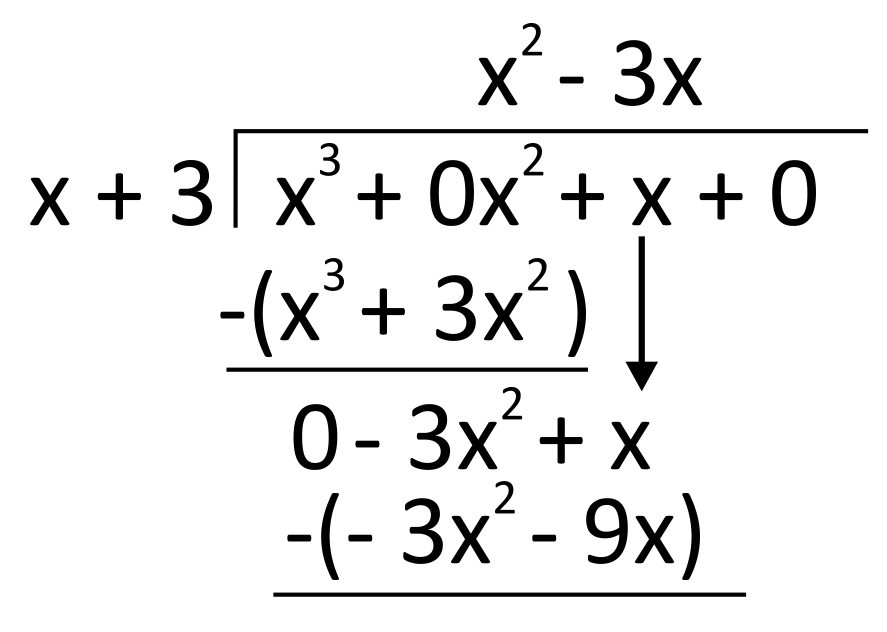
Subtract again. This leaves us with \(10x\), which we again divide by \(x\).
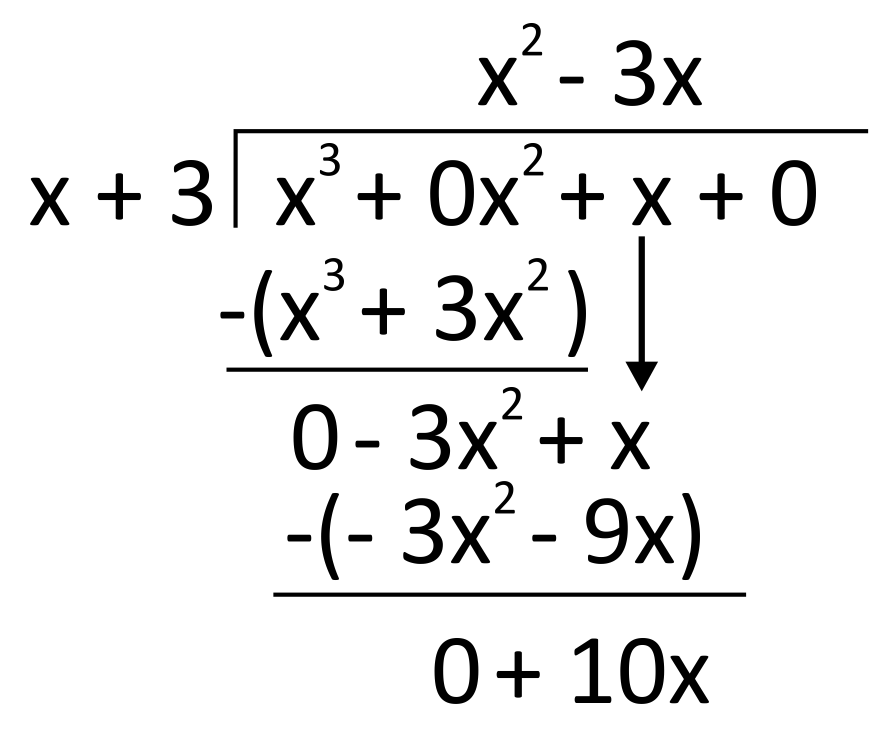
Since \(\frac{10x}{x}=10\), we write \(+10\) as the next term of the quotient, then multiply it through the divisor.
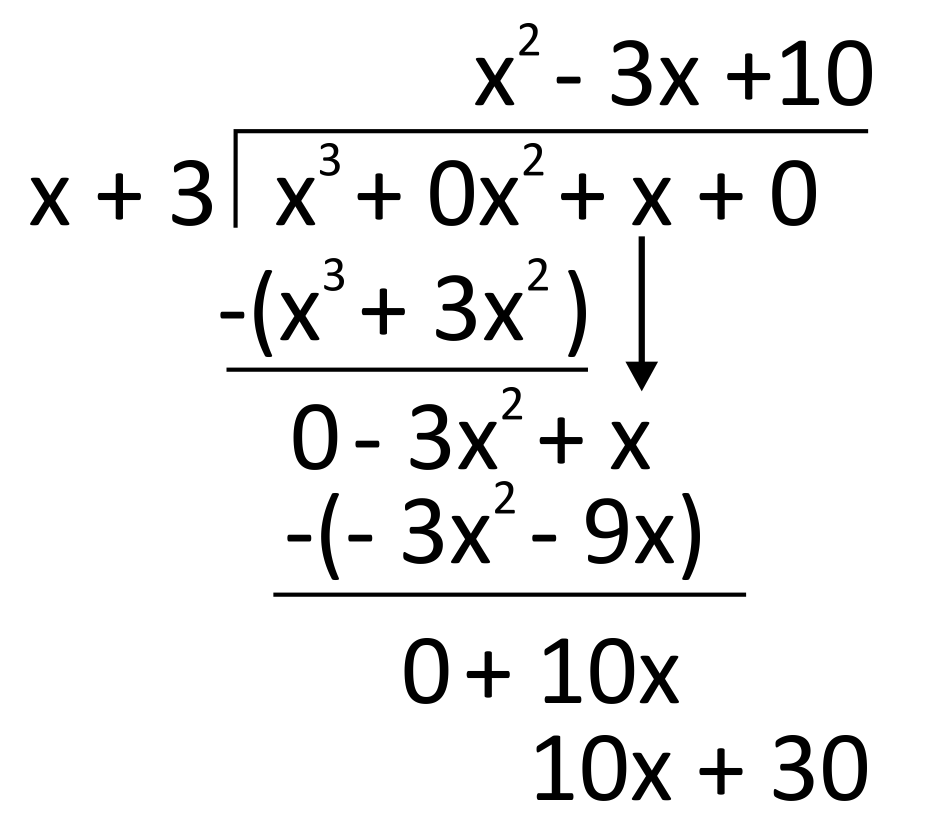
Drop down the 0-term from the dividend, draw parentheses, and subtract.
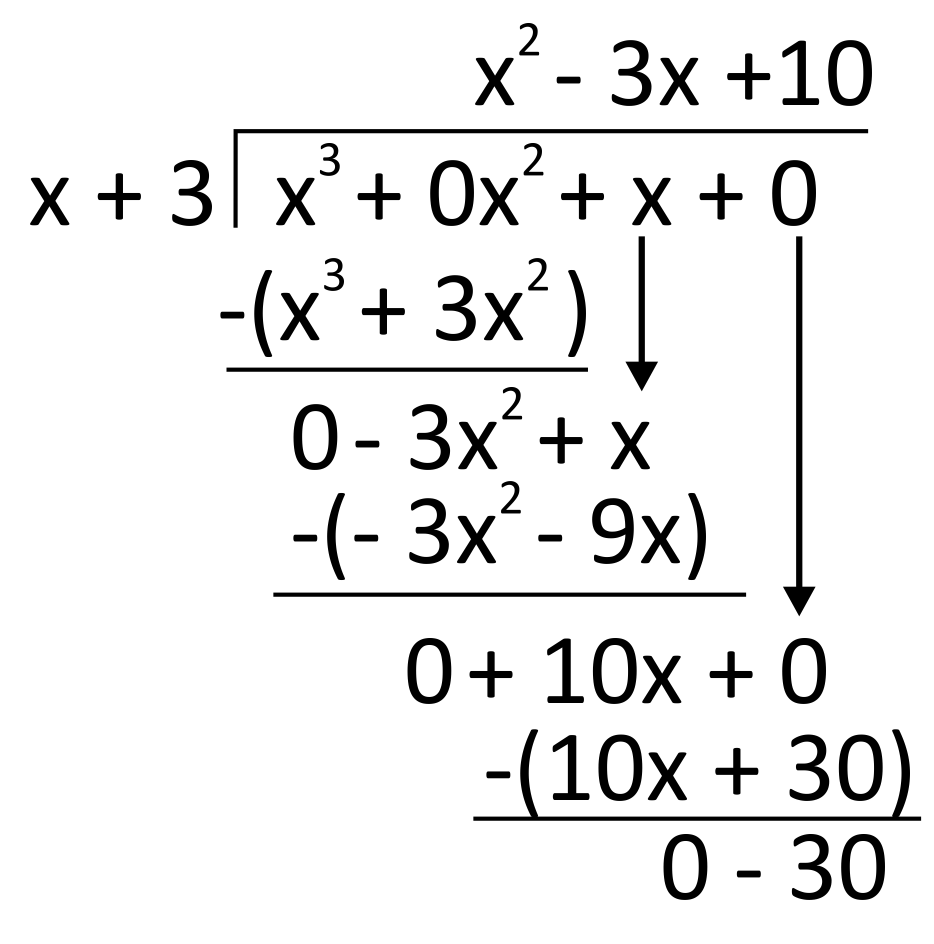
This final subtraction leaves us with a remainder term, which we write as \(\frac{-30}{x+3}\). The solution, then, is \(x^2-3x+10-\frac{30}{x+3}\). This can be verified with a multiplication check.
When there are missing terms, it is crucial to adjust the polynomial (whether the dividend or the divisor) to include the appropriate 0-coefficient terms!
Dividing Polynomials Sample Questions
Here are a few sample questions going over dividing polynomials.
Divide \(\frac{8x^3-2x+20}{4x^2}\).
Since the denominator has only one term, this fraction can be broken up into separate chunks. So \(\frac{8x^3-2x+20}{4x^2}\) becomes \(\frac{8x^3}{4x^2}-\frac{2x}{4x^2}+\frac{20}{4x^2}\). In the first term, a \(4\) and an \(x^2\) can both be factored from both the numerator and denominator, reducing the fraction to simply become \(2x\). With the second term, a \(2\) and an \(x\) can both be pulled from the top and bottom, reducing the fraction to \(-\frac{1}{2x}\). Finally, the third term can be simplified by factoring out a \(4\) from both the top and the bottom. This fraction becomes \(\frac{5}{x^2}\). The final solution comes from adding all three pieces together: \(2x-\frac{1}{2x}+\frac{5}{x^2}\).
Use long division to calculate \((3x^2-3x-6)\div(x+1)\).
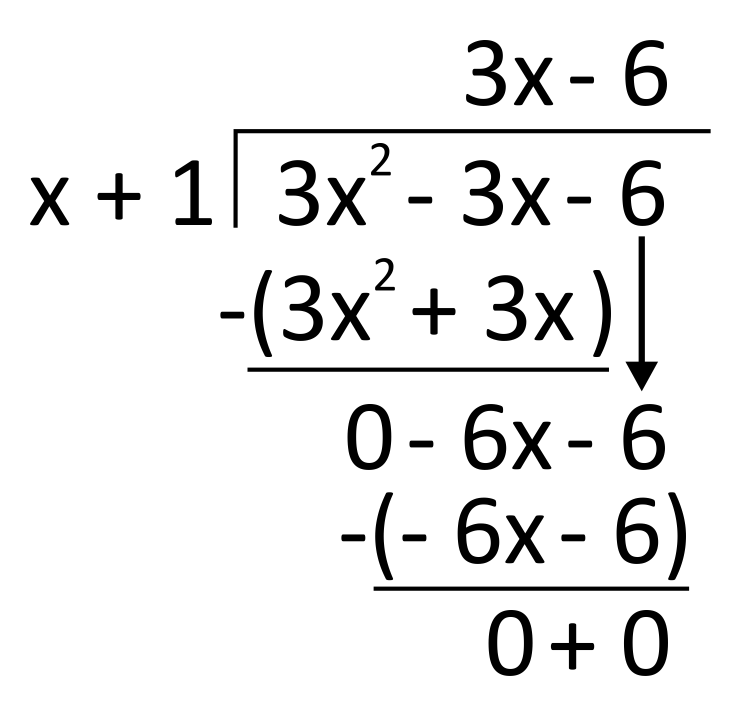
For this problem, follow the steps to divide, multiply, subtract, and repeat. Remember that it is important to draw parentheses before subtracting so that you do not make mistakes with changing signs. In this problem, there is no remainder, so the solution is simply what we have above the house: \(3x-6\).
Use long division to calculate \((20x^2-38x-30)\div(5x+3)\).
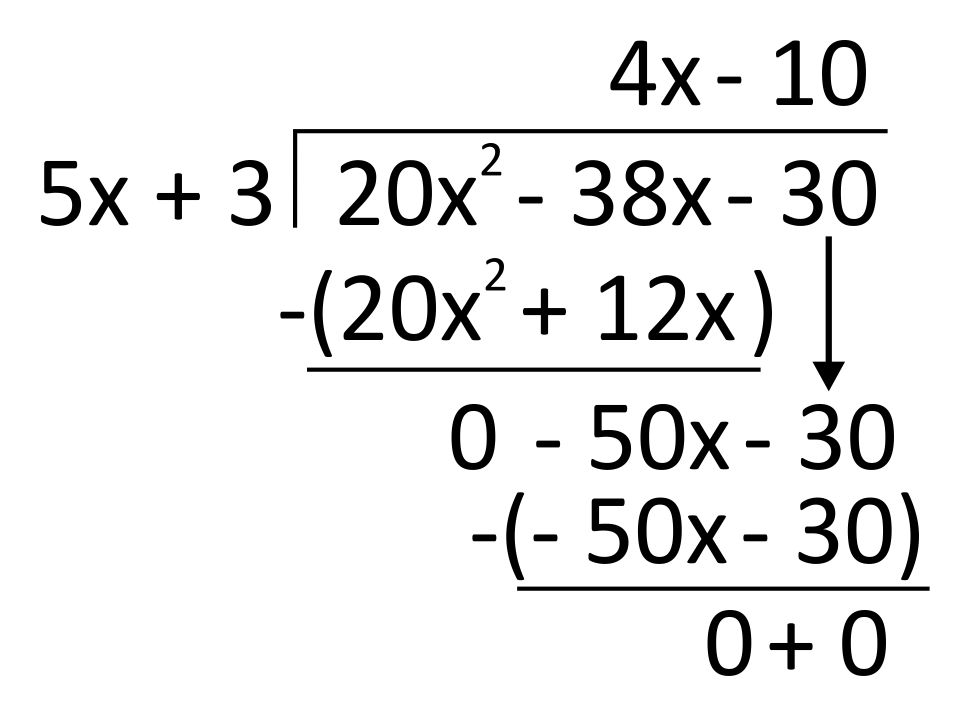
Divide, multiply, subtract, and repeat. This problem has no leftovers after the final subtraction, so there is no need to add any remainder term. The solution is given above the house: \(4x-10\).
Use long division to find the solution to \((12x^2+53x+60)\div(3x+8)\).
To solve this problem, begin with long division and cycling through the steps of division, multiplication, and subtraction. Instead of \(0\), though, the final subtraction will leave you with a leftover \(0\).
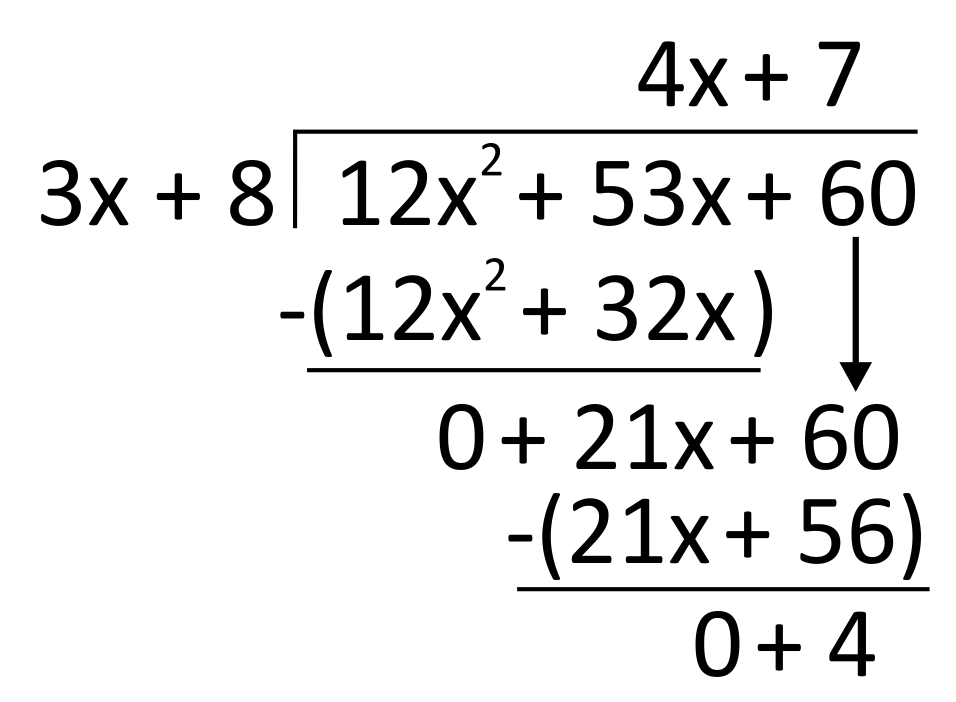
This \(4\) is part of the remainder term. We divide it by the divisor, \(3x+8\), and add this fraction to the rest of the solution to get the final answer, \(4x+7+\frac{4}{3x+8}\).
Use long division to find the solution to \((6x^2+6)\div(3x-3)\).
This can also be written as \(2x+2+\frac{4}{x-1}\). To begin, the dividend must be rewritten with a 0-coefficient \(x\)-term, \(6x^2+0x+6\). Then use long division until a positive \(12\) is left over from the final subtraction.
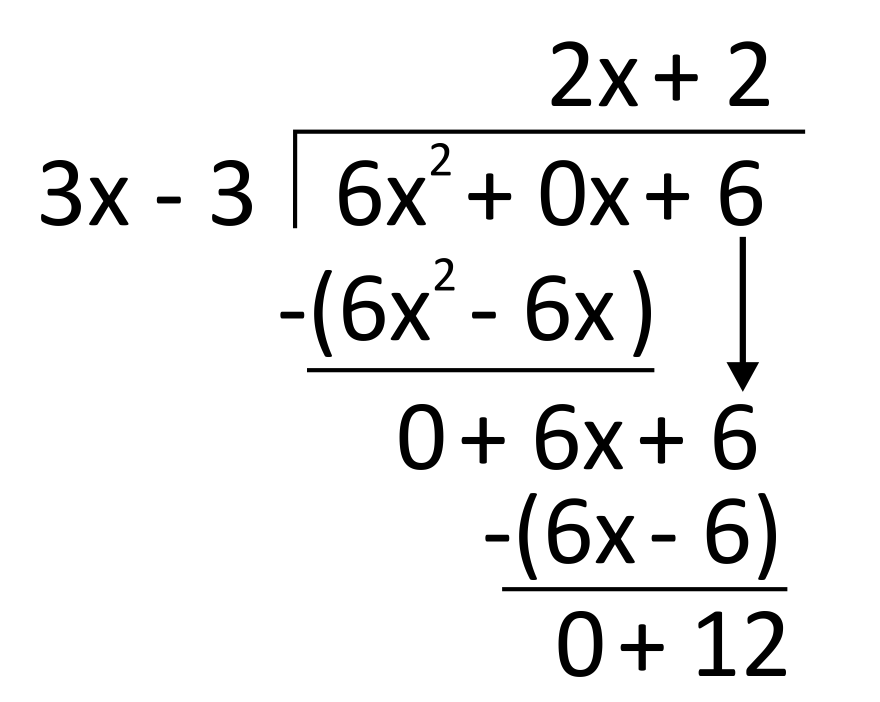
The remainder term can be found by putting the leftover \(12\) above the divisor in a fraction: \(\frac{12}{3x-3}\) or \(4x-1\), if simplified. The final solution is \(2x+2+\frac{12}{3x-3}\).