1,550+ ASVAB Practice Questions
Know Exactly How to Tackle Every Question
- Practice with 10 full-length ASVAB practice tests that mimic the actual questions you’ll find on the exam
- Master ASVAB question types so that nothing will surprise you on test day
Includes In-Depth Answer Explanations
Learn from your mistakes by understanding the questions you got wrong. Walk through their step-by-step explanation so that you nail them on test day.
“This course was very helpful, in many ways. To think that I was very bad at remembering the texts that I just read to being able to remember just about everything is unbelievable! The videos that came with this course were very insightful and explained everything in a manner that I could understand clearly.”
Benjamin
Try For 7 Days Risk-Free
Use our online course for a week
Start today and gain instant access. If you don’t think it’s for you, we’ll give your money back, no questions asked.
Start Studying
“I like how there are different learning methods within the entire course. Also, having videos and review questions help with retaining much of the information being covered.“
Lyonna
270+ ASVAB Review Videos
Difficult Topics Simplified
- Clarify concepts you don’t fully understand
- Watch ideas explained visually through animations, diagrams, and illustrations
- Listen to instructors teach difficult subjects in an understandable way
Over 25 Hours of ASVAB Video Reviews

“I felt that this course prepared me like no other course. And believe me I have tried other courses. But this one has broken it down and explained it well to me. I’m actually looking forward to my test.”
Noah
100+ ASVAB Study Lessons
A Step-By-Step Plan For Studying
- Focus only on the essential topics you need to review, without the fluff included in other courses
- Track your progress by marking lessons complete and reviewing your practice question statistics
- Highlight areas you need to brush up on with lessons adapted from our highly reviewed study guide
More Than A Textbook!
If you get tired of reading, there are several other ways to learn the material on your test. Reinforce your learning by watching videos and reviewing detailed images of the most important topics.
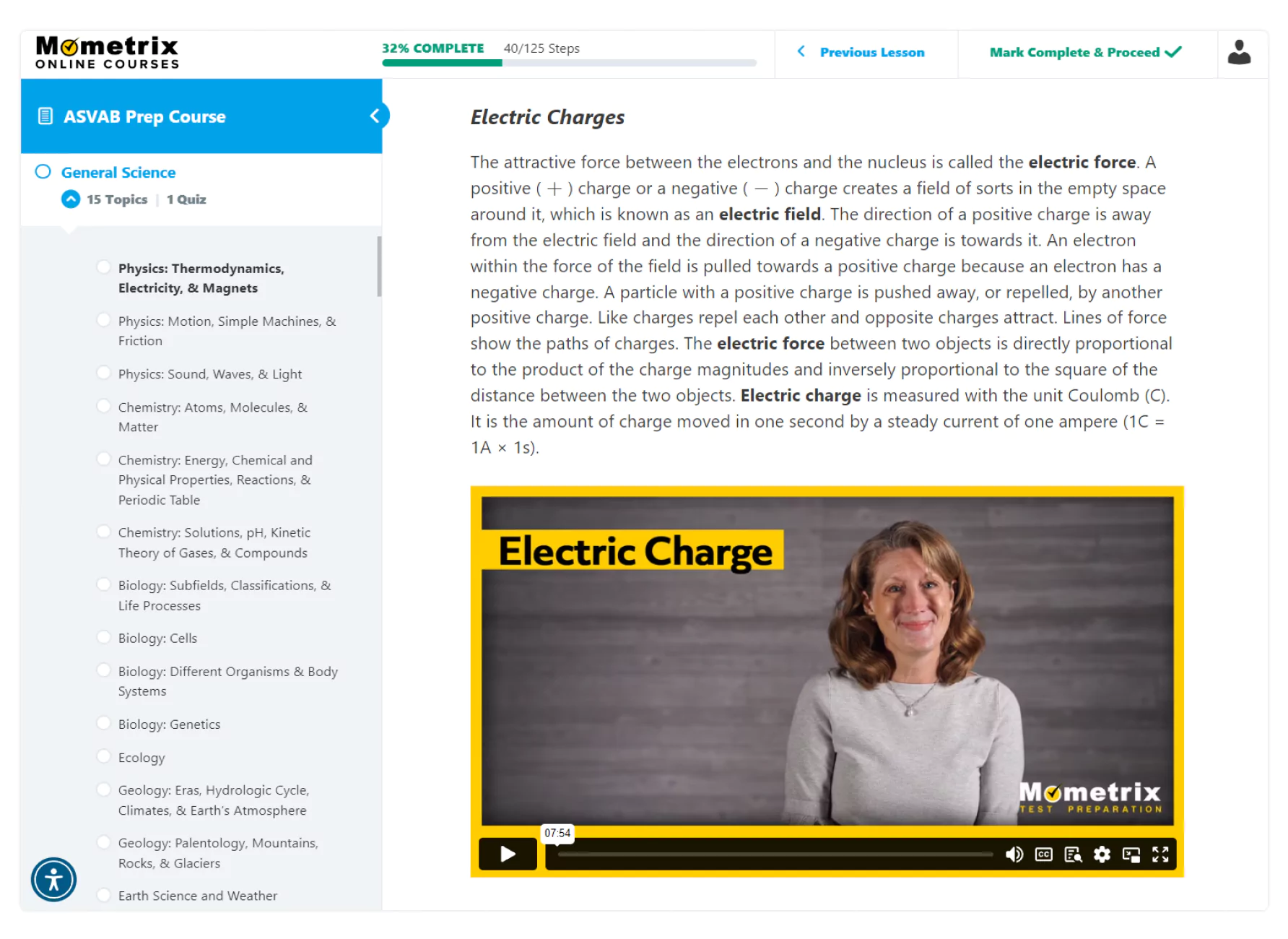
Join 6,000,000+ Students Who Use Mometrix
We’ve been down this road with millions of students before. With over 20 years of experience, you’re in the right hands.
Start Studying
Conquer the Mathematics Knowledge Section With Ease
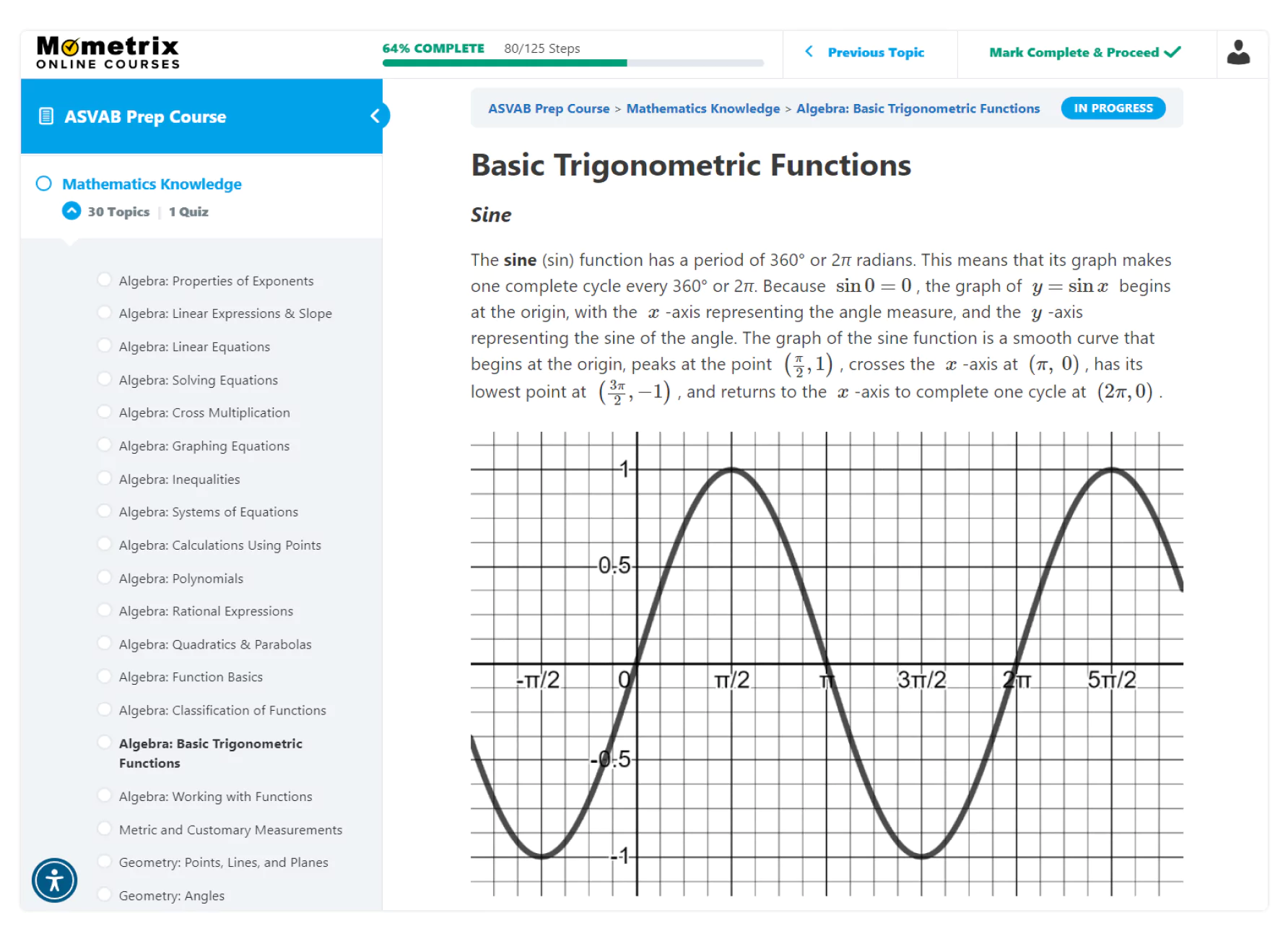
The ASVAB exam covers various math topics, from geometry to quadratics. Even the best test-takers may need a refresher on certain areas.
We understand that math, in particular, can be a stumbling block. That’s why our ASVAB prep course includes dedicated subjects to brush up on essential calculations like basic trigonometric functions, inequalities, and parabolas. We break down complex formulas into easy-to-understand steps, ensuring you feel confident tackling any math questions on the exam.
Our comprehensive course goes beyond simply memorizing the content, equipping you with the practical knowledge and skills to succeed in your career.
Use Bonus Tools and Tips
Getting a high score on the ASVAB exam requires more than just learning the material. You need to learn the test. This distinction is the biggest difference between students who get a decent score and students who get a great score.
Our course includes the secret keys to the ASVAB exam that we’ve learned through years of research. We’ll tell you how to get questions right when you have no idea what the answer is, the clues hidden in questions to help you guess correctly, and the best way to maximize your studying while minimizing your effort.

The 5 Secret Keys to ASVAB Success

Top Test-Taking Strategies

Best Study Skills

How to Overcome Test Anxiety
Prep For Every ASVAB Subject
General Science
15 Lessons | 1 Quiz
Arithmetic Reasoning
7 Lessons | 1 Quiz
Word Knowledge
3 Lessons | 1 Quiz
Paragraph Comprehension
6 Lessons | 1 Quiz
Mathematics Knowledge
30 Lessons | 1 Quiz
And more!
27 Lessons | 5 Quizzes
Frequently Asked Questions
After taking this course, you'll:
- Be familiar with the types of questions on the exam
- Fly through the exam with ease after taking our practice tests
- Use secret tips and tricks to boost your ASVAB score
- Achieve your goal of advancing your career
Take the next step in your career
39.99 /Month
7 Day Money- Back GuaranteeFeatures:
- 100+ ASVAB Lessons
- 320+ Flashcards
- 1,550+ Practice Questions
- 270+ Videos
Topics:
- General Science
- Arithmetic Reasoning
- Word Knowledge
- Paragraph Comprehension
- Mathematics Knowledge
- And more!










